
Concept explainers
a)
To calculate: The annual percentage rate and the effective annual rate
Introduction:
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a year with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
a)
Answer to Problem 77QP
The annual percentage rate is 390%, the effective annual rate is 4,197.74%
Explanation of Solution
Given information:
A check-cashing store makes a personal loan to wake-up consumers. The store offers a week loan at the rate of interest of 7.5% per week. Then, after few days, the store again makes a one-week loan at a discount interest rate of 7.5% for a week. The store also makes an add-on interest on the loan at a discount interest rate of 7.5% for a week.
Thus, if Person X borrows $100 for 4 weeks, the interest would be $33.55. As this is a discount interest rate, the net proceeding of Person X will be $66.45. Thus, Person X has to pay $100 for a month and the store also lets Person X to pay $25 in installments for a week.
Compute the annual percentage rate:
Note: The annual percentage rate is computed by multiplying the interest rate with the number of months in a year. Here, the interest is calculated per week and so the number of weeks in a year (52 weeks) is taken as the period.
Hence, the annual percentage rate is 390%
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Hence, the effective annual rate is 0.41,9774 or 4,197.74%
b)
To calculate: The annual percentage rate and the effective annual rate
Introduction:
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a year with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
b)
Answer to Problem 77QP
The annual percentage rate is 421.62%, the effective annual rate is 5,662.75%
Explanation of Solution
Given information:
A check-cashing store makes a personal loan to wake-up consumers. The store offers a week loan at the rate of interest of 7.5% per week. Then, after few days, the store again makes a one-week loan at a discount interest rate of 7.5% for a week. The store also makes an add-on interest on the loan at a discount interest rate of 7.5% for a week.
Thus, if Person X borrows $100 for 4 weeks, the interest would be $33.55. As this is a discount interest rate, the net proceeding of Person X will be $66.45. Thus, Person X has to pay $100 for a month and the store also lets Person X to pay $25 in installments for a week.
Explanation:
In the discount loan, the amount that Person X gets is reduced by the discount and Person X has to pay back the full principal value. With the discount of 7.5%, Person X receives $9.25 for each $10 as the principal value. The weekly interest rates are calculated as follows:
Note: The dollar values that are used above are not relevant. In other words, it can also be written as $0.925 and $1 or $92.5 and $100 or in any other combination that provides similar rate of interest.
Hence, the r value is 0.0811 or 8.11%
Compute the annual percentage rate:
Note: The annual percentage rate is computed by multiplying the interest rate with the number of months in a year. Here, the interest is calculated per week and so the number of weeks in a year (52 weeks) is taken as the period.
Hence, the annual percentage rate is 421.62%
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Hence, the effective annual rate is 56.6275 or 5,662.75%
c)
To calculate: The annual percentage rate and the effective annual rate
Introduction:
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a year with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
c)
Answer to Problem 77QP
The annual percentage rate is 968.19%, the effective annual rate is 717,745.21%
Explanation of Solution
Given information:
A check-cashing store makes a personal loan to wake-up consumers. The store offers a week loan at the rate of interest of 7.5% per week. Then, after few days, the store again makes a one-week loan at a discount interest rate of 7.5% for a week. The store also makes an add-on interest on the loan at a discount interest rate of 7.5% for a week.
Thus, if Person X borrows $100 for 4 weeks, the interest would be $33.55. As this is a discount interest rate, the net proceeding of Person X will be $66.45. Thus, Person X has to pay $100 for a month and the store also lets Person X to pay $25 in installments for a week.
Explanation:
In this part, the
Formula to calculate the present value annuity:
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period. Using the formulae of the present value of annuity, the interest rate is computed using the spreadsheet method.
Compute the present value annuity:
Compute the interest rate using the spreadsheet:
Step 1:

- Type the formulae of the present value annuity in H6 in the spreadsheet and consider the r value as H7
Step 2:
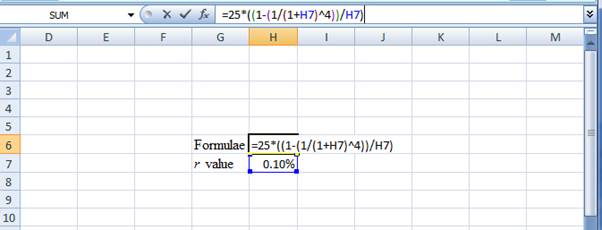
- Assume the r value as 0.10%
Step 3:
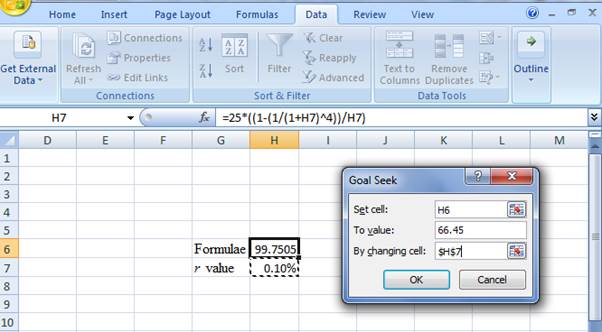
- In the spreadsheet, go to Data and select What-If-Analysis.
- Under What-If-Analysis, select Goal Seek
- In set cell, select H6 (the formula)
- The To value is considered as 66.45 (the value of the present value of annuity)
- The H7 cell is selected for the 'by changing cell.'
Step 4:
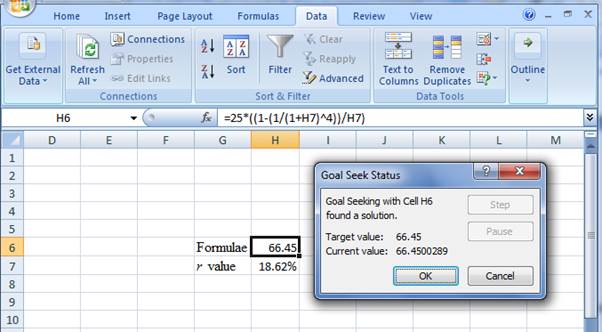
- Following the previous step, click OK in the Goal Seek Status. The Goal Seek Status appears with the r value
Step 5:
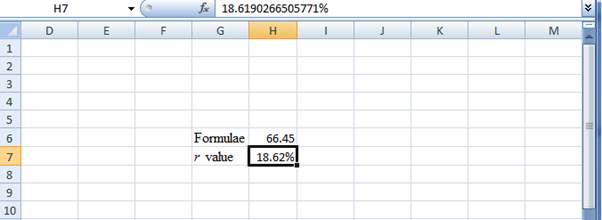
- The r value appears to be 18.6190266505771%
Hence, the r value is 18.62%
Compute the annual percentage rate:
Note: The annual percentage rate is computed by multiplying the interest rate with the number of periods in a year. Here, the interest is calculated per week and so the number of weeks in a year (52 weeks) is taken as the period.
Hence, the annual percentage rate is 968.19%
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Hence, the effective annual rate is 7,177.4521 or 717,745.21%.
Want to see more full solutions like this?
Chapter 6 Solutions
Fundamentals of Corporate Finance
- What do banks classify as NPA?arrow_forwardWhat does the payback period refer to?arrow_forwardWhich of the following bonds offers the highest current yield? a. A(n) 3.78%, 19-year bond quoted at 38.893. b. A(n) 6.30%, 28-year bond quoted at 64.822. c. A(n) 1.89%, 23-year bond quoted at 19.447. The current yield of the bond in part a is ☐ %. (Round to two decimal places.) ...arrow_forward
- Explain working capital? explain.arrow_forwardYou have the opportunity to purchase a 24-year, $1,000 par value bond that has an annual coupon rate of 11%. If you require a YTM of 7.7%, how much is the bond worth to you? The price of the bond is $ ☐ . (Round to the nearest cent.)arrow_forwardYou are considering investing $880 in Higgs B. Technology Inc. You can buy common stock at $25.88 per share; this stock pays no dividends. You can also buy a convertible bond ($1,000 par value) that is currently trading at $880 and has a conversion ratio of 30. It pays $52 per year in interest. If you expect the price of the stock to rise to $36.72 per share in one year, which instrument should you purchase? The holding period return on the purchase of the common stock would be %. (Round to two decimal places.)arrow_forward
- I need solution help by real expert and true answer.arrow_forwardAn investor is in the 24% tax bracket and lives in a state with no income tax. He is trying to decide which of two bonds to purchase. One is a(n) 9.03% corporate bond that is selling at par. The other is a municipal bond with a 6.44% coupon that is also selling at par. If all other features of these two bonds are comparable, which should the investor select? Why? Would your answer change if this were an in-state municipal bond and the investor lived in a place with high state income taxes? Explain. O A. The investor should select the corporate bond. Since the fully taxable equivalent yield of 8.47% is less than the 9.03% return on the corporate bond, the corporate issue offers a higher return and is the better buy. The decision very likely would change if this were an "in-state" municipal bond and the investor lived in a state with high income taxes. An "in-state" municipal bond would not only shield the investor from federal taxes but also from high state income taxes. OB. The…arrow_forwardHii Please solve this question by using appropriate method.arrow_forward
 EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENTPrinciples of Accounting Volume 1AccountingISBN:9781947172685Author:OpenStaxPublisher:OpenStax College
EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENTPrinciples of Accounting Volume 1AccountingISBN:9781947172685Author:OpenStaxPublisher:OpenStax College

