
Concept explainers
a)
To calculate: The annual percentage rate and the effective annual rate
Introduction:
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a year with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
a)
Answer to Problem 77QP
The annual percentage rate is 390%, the effective annual rate is 4,197.74%
Explanation of Solution
Given information:
A check-cashing store makes a personal loan to wake-up consumers. The store offers a week loan at the rate of interest of 7.5% per week. Then, after few days, the store again makes a one-week loan at a discount interest rate of 7.5% for a week. The store also makes an add-on interest on the loan at a discount interest rate of 7.5% for a week.
Thus, if Person X borrows $100 for 4 weeks, the interest would be $33.55. As this is a discount interest rate, the net proceeding of Person X will be $66.45. Thus, Person X has to pay $100 for a month and the store also lets Person X to pay $25 in installments for a week.
Compute the annual percentage rate:
Note: The annual percentage rate is computed by multiplying the interest rate with the number of months in a year. Here, the interest is calculated per week and so the number of weeks in a year (52 weeks) is taken as the period.
Hence, the annual percentage rate is 390%
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Hence, the effective annual rate is 0.41,9774 or 4,197.74%
b)
To calculate: The annual percentage rate and the effective annual rate
Introduction:
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a year with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
b)
Answer to Problem 77QP
The annual percentage rate is 421.62%, the effective annual rate is 5,662.75%
Explanation of Solution
Given information:
A check-cashing store makes a personal loan to wake-up consumers. The store offers a week loan at the rate of interest of 7.5% per week. Then, after few days, the store again makes a one-week loan at a discount interest rate of 7.5% for a week. The store also makes an add-on interest on the loan at a discount interest rate of 7.5% for a week.
Thus, if Person X borrows $100 for 4 weeks, the interest would be $33.55. As this is a discount interest rate, the net proceeding of Person X will be $66.45. Thus, Person X has to pay $100 for a month and the store also lets Person X to pay $25 in installments for a week.
Explanation:
In the discount loan, the amount that Person X gets is reduced by the discount and Person X has to pay back the full principal value. With the discount of 7.5%, Person X receives $9.25 for each $10 as the principal value. The weekly interest rates are calculated as follows:
Note: The dollar values that are used above are not relevant. In other words, it can also be written as $0.925 and $1 or $92.5 and $100 or in any other combination that provides similar rate of interest.
Hence, the r value is 0.0811 or 8.11%
Compute the annual percentage rate:
Note: The annual percentage rate is computed by multiplying the interest rate with the number of months in a year. Here, the interest is calculated per week and so the number of weeks in a year (52 weeks) is taken as the period.
Hence, the annual percentage rate is 421.62%
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Hence, the effective annual rate is 56.6275 or 5,662.75%
c)
To calculate: The annual percentage rate and the effective annual rate
Introduction:
The annual rate that is earned from the investment or charged for a borrowing is an annual percentage rate and it is also represented as APR. Thus, the APR is calculated by multiplying the rate of interest for a year with the number of months in a year. The effective annual rate is the rate of interest that is expressed as if it were compounded once in a year.
c)
Answer to Problem 77QP
The annual percentage rate is 968.19%, the effective annual rate is 717,745.21%
Explanation of Solution
Given information:
A check-cashing store makes a personal loan to wake-up consumers. The store offers a week loan at the rate of interest of 7.5% per week. Then, after few days, the store again makes a one-week loan at a discount interest rate of 7.5% for a week. The store also makes an add-on interest on the loan at a discount interest rate of 7.5% for a week.
Thus, if Person X borrows $100 for 4 weeks, the interest would be $33.55. As this is a discount interest rate, the net proceeding of Person X will be $66.45. Thus, Person X has to pay $100 for a month and the store also lets Person X to pay $25 in installments for a week.
Explanation:
In this part, the
Formula to calculate the present value annuity:
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period. Using the formulae of the present value of annuity, the interest rate is computed using the spreadsheet method.
Compute the present value annuity:
Compute the interest rate using the spreadsheet:
Step 1:

- Type the formulae of the present value annuity in H6 in the spreadsheet and consider the r value as H7
Step 2:
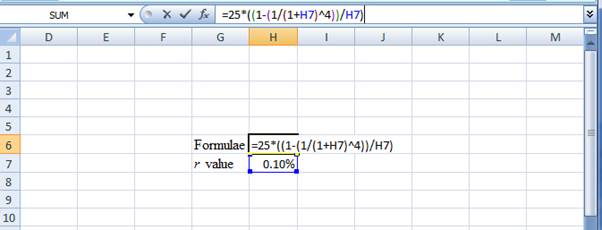
- Assume the r value as 0.10%
Step 3:
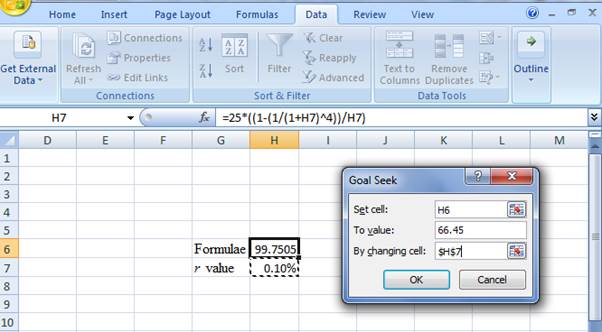
- In the spreadsheet, go to Data and select What-If-Analysis.
- Under What-If-Analysis, select Goal Seek
- In set cell, select H6 (the formula)
- The To value is considered as 66.45 (the value of the present value of annuity)
- The H7 cell is selected for the 'by changing cell.'
Step 4:
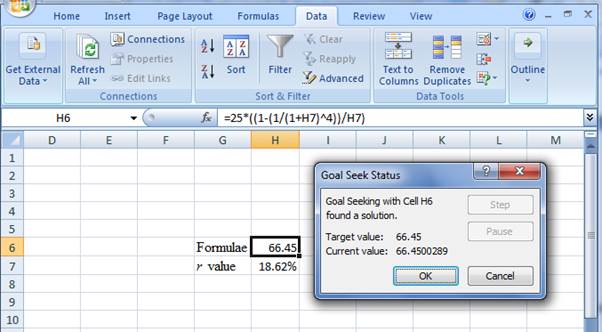
- Following the previous step, click OK in the Goal Seek Status. The Goal Seek Status appears with the r value
Step 5:
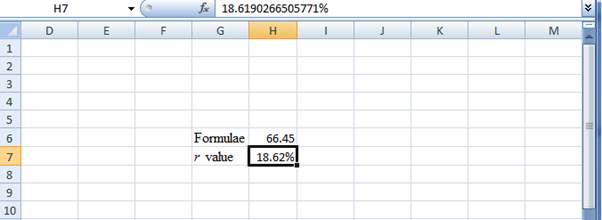
- The r value appears to be 18.6190266505771%
Hence, the r value is 18.62%
Compute the annual percentage rate:
Note: The annual percentage rate is computed by multiplying the interest rate with the number of periods in a year. Here, the interest is calculated per week and so the number of weeks in a year (52 weeks) is taken as the period.
Hence, the annual percentage rate is 968.19%
Formula to calculate the effective annual rate:
Compute the effective annual rate:
Hence, the effective annual rate is 7,177.4521 or 717,745.21%.
Want to see more full solutions like this?
Chapter 6 Solutions
Fundamentals of Corporate Finance with Connect Access Card
- If a bond has a coupon rate lower than the market interest rate, the bond will sell at:A) Par valueB) A premiumC) A discountD) Its face valuehelp.arrow_forwardIf a bond has a coupon rate lower than the market interest rate, the bond will sell at:A) Par valueB) A premiumC) A discountD) Its face valuearrow_forwardThe primary objective of financial accounting is to:a) Provide management with detailed reports for decision-making.b) Help the company save taxes.c) Provide financial information to external users.d) Track inventory levels. please help.arrow_forward
- Which of the following is an example of a capital budgeting decision?A) Determining the amount of inventory to keep on handB) Deciding whether to purchase a new piece of machineryC) Setting the credit terms for customersD) Deciding how much cash to keep in the bankarrow_forwardFor pueblo super market in st thomas usviarrow_forwardWhat is the methodology that capital markets serve as engines of economic growth and innovation? Could you help explain how methodology is critical to successful of the capital market? How are they also vulnerable to significant structural and behavioral problems? What are the appropriate uses of a qualitative single case study, and what types of research are best suited for the study of capital markets? What is the research framework of the capital market?arrow_forward
- What is the purpose of the Capital Markets? What are the qualitative research questions that Capital Markets seek to understand or explain, while quantitative research questions seek to relate or measure? What could be the problems of Capital Markets, and how can the problems of Capital Markets be solved? How can the practice or issue be improved?arrow_forwardWhat are the obstacles to work through emotional wellness coping methods, and increasing self-understanding, and how to work through them? What are the advantages and disadvantages of emotional wellness, coping methods, and increasing self-understanding?arrow_forwardWhat is the present value of $10,000 to be received in 5 years, assuming a discount rate of 10%?A) $6,210B) $6,810C) $7,580D) $8,100arrow_forward
- Depreciation is:a) The increase in the value of an asset over time.b) The allocation of the cost of a tangible asset over its useful life.c) An amount paid for the maintenance of an asset.d) An asset's market value at the end of the accounting period.arrow_forwardDepreciation is:a) The increase in the value of an asset over time.b) The allocation of the cost of a tangible asset over its useful life.c) An amount paid for the maintenance of an asset.d) An asset's market value at the end of the accounting period. Need helparrow_forwardWhat is the corporate finance how this is the part of finance?arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





