
Calculating
a. If she starts making these deposits on her 36th birthday and continues to make deposits until she is 65 (the last deposit will be on her 65th birthday), what amount must she deposit annually to be able to make the desired withdrawals at retirement?
b. Suppose your friend has just inherited a large sum of money. Rather than making equal annual payments, she has decided to make one lump sum payment on her 35th birthday to cover her retirement needs. What amount does she have to deposit?
c. Suppose your friend’s employer will contribute $3,500 to the account every year as part of the company’s profit-sharing plan. In addition, your friend expects a $175,000 distribution from a family trust fund on her 55th birthday, which she will also put into the retirement account. What amount must she deposit annually now to be able to make the desired withdrawals at retirement?
a)
To calculate: The required savings for each year
Introduction:
The series of payments that are made in equal intervals is an annuity payment. The amount of annuity payments is mainly calculated based on the particular situation.
Answer to Problem 68QP
The required savings for each year is $11,776.01
Explanation of Solution
Given information:
Person X’s friend is celebrating her 35th birthday today as she wishes to start saving for her retirement at the age of 65. She wants to withdraw a sum of $105,000 on each of her birthdays for 20 years that is followed by her retirement in which, the first withdrawal will fall on her 66th birthday. She also intends to put her money in the local credit union that offers a 7% interest for a year. She also wishes to make equivalent annual payments on each of her birthdays into the account that is established at the Credit Union for retirement fund.
It is assumed that she starts making the deposit on her 36th birthday and continues to make it until her 65th birthday.
Timeline of the amount that is necessary for retirement is as follows:
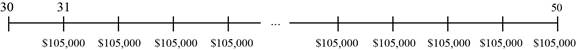
Note: In the above given information, every question is asked for a different cash flow but it is for the funding of the same retirement plan. Each of the saving possibility has the similar future value that refers to the present value of the spending on the retirement when Person X’s friend is ready for the retirement.
Formula to calculate the present value annuity is as follows:
Note: C denotes the payments, r denotes the rate of exchange, and t denotes the period. Thus, by the present value of annuity, the amount that is essential for Person X’s friend is when she is ready for the retirement and it can be calculated as follows:
Compute the present value annuity:
Hence, the amount that is required for Person X’s friend at the time of retirement is $1,112,371.50
Note: The present value of annuity is same for all the necessary requirements.
The timeline that denotes when Person X’s friend makes equivalent annual deposits into the account and with the future value of annuity equivalent to the sum essential at the time of retirement is as follows:

Formula to calculate the future value annuity is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments. The future value of annuity represents the necessary savings for each year.
Compute the future value annuity:
Hence, the required savings for each year is $11,776.01.
b)
To calculate: The present value of the lump sum savings
Introduction:
The series of payments that are made in equal intervals is an annuity payment. The amount of annuity payments is mainly calculated based on the particular situation.
Answer to Problem 68QP
The present value of the lump sum savings is $146,129.04
Explanation of Solution
Given information:
Person X’s friend is celebrating her 35th birthday today as she wishes to start saving for her retirement at the age of 65. She wants to withdraw a sum of $105,000 on each of her birthdays for 20 years that is followed by her retirement in which, the first withdrawal will fall on her 66th birthday. She also intends to put her money in the local credit union that offers a 7% interest for a year. She also wishes to make equivalent annual payments on each of her birthdays into the account that is established at the Credit Union for retirement fund.
Person X’s friend has just inherited a large sum of money. She decides to make the lump sum payment on her 35th birthday to cover the needs of retirement rather than making equal annual payments.
Timeline for the lump sum saving amount is as follows:

Formula to compute the future value is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value:
Hence, the lump sum amount is $146,129.04
c)
To calculate: The annual contribution of Person X’s friend
Introduction:
The series of payments that are made in equal intervals is an annuity payment. The amount of annuity payments is mainly calculated based on the particular situation.
Answer to Problem 68QP
The annual contribution of Person X’s friend is $4,631.63
Explanation of Solution
Given information:
Person X’s friend is celebrating her 35th birthday today as she wishes to start saving for her retirement at the age of 65. She wants to withdraw a sum of $105,000 on each of her birthdays for 20 years that is followed by her retirement in which, the first withdrawal will fall on her 66th birthday. She also intends to put her money in the local credit union that offers a 7% interest for a year. She also wishes to make equivalent annual payments on each of her birthdays into the account that is established at the Credit Union for retirement fund.
The employer of Person X’s friend contributes a sum of $3,500 into her account each year as a part of sharing the profit. In addition, Person X’s friend also expects a sum of distribution from her family trust on her 55th birthday that amounts to $175,000.
Timeline of the lump sum saving in addition to the annual deposit is as follows:

Note: The value that is essential for retirement is known as the value of the lump sum saving at retirement can be subtracted to determine how much Person X’s friend is short of.
Formula to compute the future value of the trust fund deposit is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value of the trust fund deposit is as follows:
Hence, the future value of the trust fund deposit is $344,251.49.
The amount that Person X’s friend needs at retirement is calculated as follows:
Hence, the amount that Person X’s friend needs at the time of retirement is $768,120.01.
Note: The payment can be solved by using the equation of the future value of annuity.
Formula to calculate the future value annuity is as follows:
Note: C denotes the annual cash flow or annuity payment, r denotes the rate of interest, and t denotes the number of payments.
Compute the future value annuity:
Hence, the total annual contribution is $8,131.63
Compute the contribution that is made by Person X’s friend is as follows:
Note: The contribution made by Person X’s friend is calculated by subtracting the employer’s contribution from the total annual contribution.
Hence, the contribution made by Person X’s friend is $4,631.63.
Want to see more full solutions like this?
Chapter 6 Solutions
Connect 1 Semester Access Card for Fundamentals of Corporate Finance
 EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK CONTEMPORARY FINANCIAL MANAGEMENTFinanceISBN:9781337514835Author:MOYERPublisher:CENGAGE LEARNING - CONSIGNMENT

