
Concept explainers
(a)
The production process without capital input.
(a)
Explanation of Solution
A production function of a firm shows the relationship between the output and two inputs, capital and labor. In this case, the firm follows the Cobb‑Douglas production function.
Here, this production function clearly shows that the firm produces the output using the inputs, capital, and labor at an equal proportion. Therefore, producer cannot build any coffee tables without tools (capital). If did so, the output would be zero.
(b)
The production process without labor input.
(b)
Explanation of Solution
As described in part (a), the firm follows the Cobb‑Douglas production function where the firm uses the inputs, capital, and labor at an equal proportion to produce the given level of output. Therefore, the producer cannot build any coffee tables without labor inputs. If did so, the output would be zero.
(c)
The short run production function.
(c)
Explanation of Solution
The production economies state that the short-run is the period of time during which one or more inputs into production cannot be changed, which mean that the short run production function of a firm holds variable inputs as well as fixed inputs. Therefore, the short run production function shows the output as a function of variable input and the fixed input.
In this case, the fixed input, capital, is given as 16. Now substitute the respective value into the given Cobb‑Douglas production function to get the short run production function of the firm.
Therefore, the short run production function is
Fixed inputs: The fixed inputs are inputs that cannot be changed in the short run
Variable inputs: The variable inputs are inputs that can be changed in the short run.
(d)
The graphical representation of the production function.
(d)
Explanation of Solution
Short run production function is given below (Derived in subpart (c)).
Substitute the labor of 1 unit in Equation (1) to calculate the output at that particular level.
In the short run, output with one unit of labor is 16 units.
Table 1 shows the output of different levels of labor.
Table 2
| Labor | Output |
| 1 | 16 |
| 4 | 32 |
| 9 | 48 |
| 16 | 64 |
| 25 | 80 |
Figure 1 shows the short-run production function.
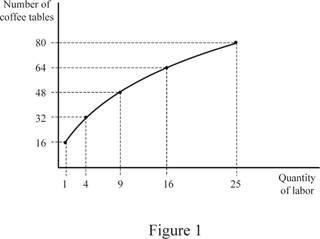
In Figure 1, the vertical axis shows the output and the horizontal axis shows the quantity of labor inputs. The production curve shows the possible level of output with different labor quantities.
(e)
The average and marginal product of labor.
(e)
Explanation of Solution
The marginal product can be calculated using the following equation.
Now substitute the respective in Equation (1) to get the value of marginal product at 4 units of labor inputs.
Therefore, the value of marginal product at 4 units of labor is 5.33.
The average product can be calculated using the following equation.
Now substitute the respective values in Equation (3) to get the value of average product at 4 units of labor inputs.
Therefore, the value of the average product at 4 units of labor is 8.
Table 2 shows the values of total product, marginal product, and average product using Equations (1), (2), and (3).
Table 2
|
Number of workers | Total product | Marginal product | Average product |
| 1 | 16 | 16 | 16 |
| 4 | 32 | 5.33 | 8 |
| 9 | 48 | 3.2 | 5.33 |
| 16 | 64 | 2.29 | 4 |
| 25 | 80 | 1.78 | 3.2 |
Marginal product: A marginal product is the additional output that a firm can produce using an additional unit of an input, holding use of the other input constant.
Average product: An average product is the quantity of output produced per unit of input.
(f)
The total product, average product, and marginal product.
(f)
Explanation of Solution
In this case, the capital was fixed at 16 units. If there is a fall of 7 machines, then the capital will be 9
Therefore, the new short run production function is
Table 3 shows the values of total product, marginal product, and average product at each level of new output using equation (1), (2), and (3).
Table 3
|
Number of workers | Total product | Marginal product | Average product |
| 1 | 12 | 12 | 12 |
| 4 | 24 | 4 | 6 |
| 9 | 36 | 2.4 | 4 |
| 16 | 48 | 1.71 | 3 |
| 25 | 60 | 1.33 | 2.4 |
Total product: The total product is the total quantity of output produced by a firm at the given time period.
Average product: An average product is the quantity of output produced per unit of input.
Marginal product: A marginal product is the additional output that a firm can produce using an additional unit of an input.
Want to see more full solutions like this?
Chapter 6 Solutions
Microeconomics
- how to solve the attachment?arrow_forwardProblem 3-ABC Challenges: Attrition, Balance and ComplianceCan television inform people about public affairs? Political scientists Bethany Albertson and Adria Lawrence (2009) conducted an experiment in which they randomly assigned people to treatment and control groups to evaluate the effect of watching TV on a person’s information level. Those assigned to the treatment group were told to watch a specific television broadcast and were later asked questions related to what they watched. Those in the controlgroup were not shown the TV broadcast but were asked questions related to the material in the TV broadcast. The dataset contains the following variables: : Dummy variable which =1 if a person reads news and 0 otherwise. : interest in political affairs (not interested=1 to very interested=4) : years of education : female dummy variable (female=1; male=0) : family income in thousands of dollars : information level (low information level=1 to high information level=4) =1 if the…arrow_forwardProblem 2-Experiments/Randomized Control Trial Suppose you are interested in studying the effect of academic counselling on the years it takes for a student to obtain an undergraduate degree. You conduct a randomized control trial to answer the question. You randomly assign 2500 individuals in a university in New York to receive academic counselling and 2500 students to not receive any academic counselling. a. Which people are a part of the treatment group and which people are a part of thecontrol group? b. What regression will you run? Define the variables where required. c. Suppose you estimate = -0.3. Interpret it. d. You test for balance using the variables mentioned in the table below. Based on the results do you think that the treatment and control group are balanced? If your answer is “yes” then explain why. If your answer is “no”, then explain why and mention how will you address the issue of imbalance. e. Suppose that some unmotivated students in the control group decided to…arrow_forward
- How to calculate total cost?arrow_forwardProblem 1-Experiments/Randomized Control TrialSuppose you are interested in studying the effect of being a part of the labor union on anindividual’s hourly wage.You collect data on 1000 people and run the following regression. where is a dummy variable which is equal t to 1 for people who are a part of labor union and0 for others. a. Suppose you estimate . Interpret b. Do you think is biased or unbiased? Explain. Now suppose you conduct a randomized control trial to answer the same question. Yourandomly assign some individuals to be a part of the labor union and others to not be a partof the labor union. The first step you take is to ensure that the randomization was donecorrectly. Then you estimate the following equation: =1 if the student is assigned to be a part of Labor Union=0 if the student is assigned to not be a part of Labor Union c. Why is it important to ensure that the randomization is done correctly? d. Name any two variables that you can use to test if Treatment and…arrow_forwardWhat is kiosk?arrow_forward
- If food is produced in the U.S., sold in the U.S. and consumed in the U.S., a reduction in its price will have which of the following effects ______? Two of the answers are correct. The consumer price index will decrease. None of the answers are correct. The GDP deflator will decrease.arrow_forwardhow to caculate verible cost?arrow_forwardWhat is the deficit?arrow_forward
- Identify the two curves shown on the graph, and explain their upward and downward slopes. Why does curve Aintersect the horizontal axis? What is the significance of quantity d? What does erepresent? How would the optimal quantity of information change if the marginal benefit of information increased—that is, if the marginal benefit curve shifted upward?arrow_forward6. Rent seeking The following graph shows the demand, marginal revenue, and marginal cost curves for a single-price monopolist that produces a drug that helps relieve arthritis pain. Place the grey point (star symbol) in the appropriate location on the graph to indicate the monopoly outcome such that the dashed lines reveal the profit-maximizing price and quantity of a single-price monopolist. Then, use the green rectangle (triangle symbols) to show the profits earned by the monopolist. 18 200 20 16 16 14 PRICE (Dollars per dose) 12 10 10 8 4 2 MC = ATC MR Demand 0 0 5 10 15 20 25 30 35 40 45 50 QUANTITY (Millions of doses per year) Monopoly Outcome Monopoly Profits Suppose that should the patent on this particular drug expire, the market would become perfectly competitive, with new firms immediately entering the market with essentially identical products. Further suppose that in this case the original firm will hire lobbyists and make donations to several key politicians to extend its…arrow_forwardConsider a call option on a stock that does not pay dividends. The stock price is $100 per share, and the risk-free interest rate is 10%. The call strike is $100 (at the money). The stock moves randomly with u=2 and d=0.5. 1. Write the system of equations to replicate the option using A shares and B bonds. 2. Solve the system of equations and determine the number of shares and the number of bonds needed to replicate the option. Show your answer with 4 decimal places (x.xxxx); do not round intermediate calculations. This is easy to do in Excel. A = B = 3. Use A shares and B bonds from the prior question to calculate the premium on the option. Again, do not round intermediate calculations and show your answer with 4 decimal places. Call premium =arrow_forward

 Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON
Principles of Economics (12th Edition)EconomicsISBN:9780134078779Author:Karl E. Case, Ray C. Fair, Sharon E. OsterPublisher:PEARSON Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON
Engineering Economy (17th Edition)EconomicsISBN:9780134870069Author:William G. Sullivan, Elin M. Wicks, C. Patrick KoellingPublisher:PEARSON Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning
Principles of Economics (MindTap Course List)EconomicsISBN:9781305585126Author:N. Gregory MankiwPublisher:Cengage Learning Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education
Managerial Economics & Business Strategy (Mcgraw-...EconomicsISBN:9781259290619Author:Michael Baye, Jeff PrincePublisher:McGraw-Hill Education





