
To expand the
CAT is required to send invoice to each participant. The details of invoice should be classes in which participant is enrolled, total fee for the adventure classes, name and address of participant.
Given information:
Following database design was developed for exercise 3:
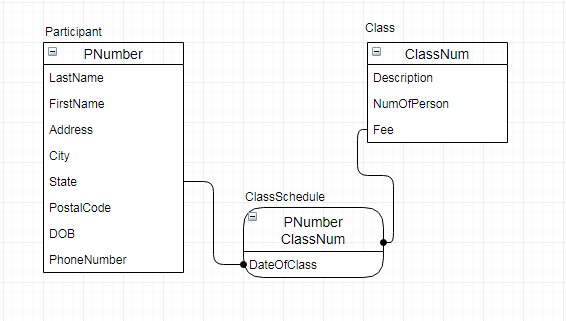
Explanation:
Based on user view following Invoice table should be generated:
Invoice (InvoiceNum, ClassNum, TotalFees, LastName, FirstName, Address)
In the above relation attributes LastName, FirstName and Address are already present in Participant table. Thus, only by including the PNumber as foreign key in Invoice table one should be able to get last name, first name and address of the participant. Therefore, Invoice relations should have the following structure:
Invoice (InvoiceNum, ClassNum, TotalFees, PNumber)

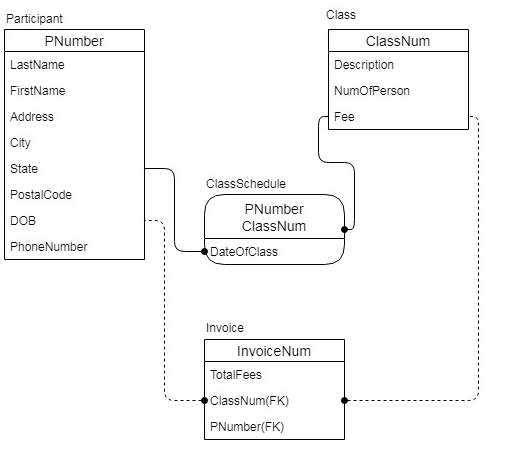
Thus, DBDL for this user view will be as follows:
Cumulative design after this user view will be as follows:
Trending nowThis is a popular solution!

Chapter 6 Solutions
Concepts of Database Management
- I need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardI need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardHello, Please read the provided text carefully—everything is detailed there. I need high-quality diagrams for both cases: Student A and Student B, showing the teacher teaching them through knowledge distillation. Each case should be represented as a separate image. The knowledge distillation process must be clearly illustrated in both. I’ve attached an image that shows the level of clarity I’m aiming for. Please do not use AI-generated diagrams. If I wanted that, I could do it myself using ChatGPT Premium. I’m looking for support from a real human expert—and I know you can help. " 1. Teacher Model Architecture (T) Dataset C: Clean data with complete inputs and labels Architecture Input Embedding Layer Converts multivariate sensor inputs into dense vectors. Positional Encoding Adds time-step order information to each embedding. Transformer Encoder Stack (repeated N times) Multi-Head Self-Attention: Captures temporal dependencies across time steps. Add…arrow_forward
- (connection)? Q1: Define the BGP ? Ebgp vs I bgp, and how do I advertise? With a drawing example QT: Explain how to make messages in the BGP protocol. Q: What is concept the hot potato routing in BGP? Q: What are the criteria for BGP route selection? Qo: Define the concept of Spanning Tree Protocol. Explain in detail and draw the figures. Q1: What happens when STP is disabled? QV: Define the concept of broadcast storm. QA: List and explain the Steps to a Loop-Free Topology when using the Spanning Tree Algorithm and Spanning Tree Protocol in a four-step process. I want a typical and concise Solutionarrow_forwardWATCH THE VIDEO ABOUT MODELLING OR SPECIFICATION PHASE AND ANSWER THE FOLLOWING QUESTIONS: https://www.youtube.com/watch?v=uoIxDeAyfdo 1.- DEFINE SPECIFICATION OR MODELLING 2.- WRITE DOWN THE 3 REQUIREMENTS SPECIFICATION TECHNIQUES OR FORMATS 3.-DEFINE USE CASES 4.-DEFINE SRS 5.-DEFINE USER STORIES 6.- IS IT RECOMMENDABLE TO USE SRS DOCUMENTS IN AGILE METHODOLOGY? WHY? 7.- HOW DO YOU KNOW WHICH TECHNIQUE OR FORMAT TO USE? 8.- WRITE DOWN THE USE CASE COMPONENTSarrow_forwardREADING AND LISTENING ACTIVITIES BASED ON THE VIDEO: “REQUIREMENT ELICITATION “ Watch the following video and look for the answer to the following questions: https://www.youtube.com/watch?v=pSQRetBoaRE&t=24s 1.-NAME THE 2 PHASES OF THE REQUIREMENT ENGINEERING PROCESS 2.-NAME AT LEAST 7 ELICITATION TECHNIQUES TO COLLECT THE INFORMATION REQUIRED 3.-REFER TO THE NUMBER OF QUESTIONS AND TYPE OF QUESTIONS THAT SHOULD BE ASKED TO THE DIFFERENT STAKEHOLDERS. 4.-NAME THE DIFFERENT TYPES OF PROBLEMS YOU CAN ENCOUNTER DURING THE REQUIREMENT ELICITATION PROCESS 5.- ACCORDING TO THE VIDEO, WHICH TYPES OF TECHNIQUES SHOULD YOU USE, WHICH ONES WOULD YOU USE ACCORDING TO PROFESSOR SHERRIFF ‘S RECOMMENDATIONS?arrow_forward
- Can you please show me how I can do this on google sheets. For the spreadsheet you need to create a multi page sheets thing that uses all the techniques of counts/sums and graph showing how many contracts have been returned for each grade...you can make up the data (let's say in grade 9 I got 15 contracted back with fake data that I want you to show me how to create on google spreadsheet) For grade 10 i got 20 contracts signed, for grade 11 I got 16 contracts and for grade 12 I got 25 contracts back. Can you help me pls. Thanks so much. Make sure you have graphs on the page and also the sum written as a formula and the numbers filled in the columns.arrow_forwardI need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardGoal: Understand how to build a concurrent server and deal with signals Description: Use TCP socket programming in C to implement a pair of client and server programs. The client simply asks the user to enter a string (null-terminated), and then displays a menu for the user to select an operation on that string. The string and the type of operation are sent to the child server which performs the required operation and returns the result back to the client. That is, the server (parent) creates a child for each request of the client (you need to print the port and IP address of the client on the server terminal). Then it waits for the child to finish processing client's request and prints the process ID of the terminated child. The connection between your client and server should stay open, so that the client can send another request. However, the exit will happen when the user sends the client program the SIGQUIT signal. The handler will print a notifying message (for example, "Good…arrow_forward
- I need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardI need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardI need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forward
 Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY





