
Concept explainers
A golfer tees off from a location precisely at ϕi = 35.0° north latitude. He hits the ball due south, with range 285 m. The ball’s initial velocity is at 48.0° above the horizontal. Suppose air resistance is negligible for the golf ball. (a) For how long is the ball in flight? The cup is due south of the golfer’s location, and the golfer would have a hole-in-one if the Earth were not rotating. The Earth’s rotation makes the tee move in a circle of radius RE cos ϕi = (6.37 × 106 m) cos 35.0° as shown in Figure P6.47. The tee completes one revolution each day. (b) Find the eastward speed of the tee relative to the stars. The hole is also moving cast, but it is 285 m farther south and thus at a slightly lower latitude ϕf. Because the hole moves in a slightly larger circle, its speed must he greater than that of the tee. (c) By how much does the hole’s speed exceed that of the tee? During the time interval the ball is in flight, it moves upward and downward as well as southward with the projectile motion you studied in Chapter 4, but it also moves eastward with the speed you found in part (b). The hole moves to the east at a faster speed, however, pulling ahead of the ball with the relative speed you found in part (c). (d) How far to the west of the hole does the ball land?
Figure P6.47
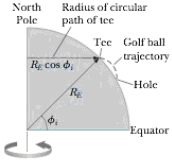
(a)
The time of flight of the ball.
Answer to Problem 47CP
The time for which the ball be in flight is
Explanation of Solution
The range of the motion after hitting the ball is
The range of the parabolic motion
Here,
Write the expression for the equation for parabolic motion
As initial and final distance is equal,
Rearrange the above expression for
Substitute
Rearrange the above expression for
Substitute
Conclusion:
Substitute
Therefore, the time for which the ball be in flight is
(b)
The relative eastward speed of the tee with respect to the stars.
Answer to Problem 47CP
The relative eastward speed of the tee with respect to the stars is
Explanation of Solution
Write the formula to calculate the eastward speed of the tee relative to the stars
Here,
Conclusion:
Substitute
Therefore, the relative eastward speed of the tee with respect to the stars is
(c)
The value by which the hole's speed exceed that of the tee.
Answer to Problem 47CP
The value by which the hole's speed exceed that of the tee is
Explanation of Solution
Write the formula to calculate the length of the arc
Rearrange the above expression for
Substitute
Write the formula to calculate the speed of the hole
Here,
Substitute
Calculate the difference between the speed of tee and the speed of hole.
Here,
Conclusion:
Substitute
Therefore, the value by which the hole's speed exceed that of the tee is
(d)
The distance to the west of the hole from the position where the ball lands.
Answer to Problem 47CP
The distance to the west of the hole from the position where the ball land is
Explanation of Solution
Write the expression for the distance to west of the hole
Here,
Conclusion:
Substitute
Therefore, the distance to the west of the hole from the position where the ball land is
Want to see more full solutions like this?
Chapter 6 Solutions
PHYSICS:F/SCI.+ENGRS.(LL)-W/WEBASSIGN
- Mick and Rick are twins born on Earth in the year 2175. Rick grows up to be an Earth-bound robotics technician while Mick becomes an intergalactic astronaut. Mick leaves the Earth on his first space mission in the year 2200 and travels, according to his clock, for 10 years at a speed of 0.75c. Unfortunately, at this point in his journey, the structure of his ship undergoes mechanical breakdown and the ship explodes. How old is Rick when his brother dies?arrow_forwardHi, I have canceled, why did you charge me again?arrow_forwardNo chatgpt pls will upvotearrow_forward
- For each of the actions depicted below, a magnet and/or metal loop moves with velocity v→ (v→ is constant and has the same magnitude in all parts). Determine whether a current is induced in the metal loop. If so, indicate the direction of the current in the loop, either clockwise or counterclockwise when seen from the right of the loop. The axis of the magnet is lined up with the center of the loop. For the action depicted in (Figure 5), indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop). I know that the current is clockwise, I just dont understand why. Please fully explain why it's clockwise, Thank youarrow_forwardA planar double pendulum consists of two point masses \[m_1 = 1.00~\mathrm{kg}, \qquad m_2 = 1.00~\mathrm{kg}\]connected by massless, rigid rods of lengths \[L_1 = 1.00~\mathrm{m}, \qquad L_2 = 1.20~\mathrm{m}.\]The upper rod is hinged to a fixed pivot; gravity acts vertically downward with\[g = 9.81~\mathrm{m\,s^{-2}}.\]Define the generalized coordinates \(\theta_1,\theta_2\) as the angles each rod makes with thedownward vertical (positive anticlockwise, measured in radians unless stated otherwise).At \(t=0\) the system is released from rest with \[\theta_1(0)=120^{\circ}, \qquad\theta_2(0)=-10^{\circ}, \qquad\dot{\theta}_1(0)=\dot{\theta}_2(0)=0 .\]Using the exact nonlinear equations of motion (no small-angle or planar-pendulumapproximations) and assuming the rods never stretch or slip, determine the angle\(\theta_2\) at the instant\[t = 10.0~\mathrm{s}.\]Give the result in degrees, in the interval \((-180^{\circ},180^{\circ}]\).arrow_forwardWhat are the expected readings of the ammeter and voltmeter for the circuit in the figure below? (R = 5.60 Ω, ΔV = 6.30 V) ammeter I =arrow_forward
- simple diagram to illustrate the setup for each law- coulombs law and biot savart lawarrow_forwardA circular coil with 100 turns and a radius of 0.05 m is placed in a magnetic field that changes at auniform rate from 0.2 T to 0.8 T in 0.1 seconds. The plane of the coil is perpendicular to the field.• Calculate the induced electric field in the coil.• Calculate the current density in the coil given its conductivity σ.arrow_forwardAn L-C circuit has an inductance of 0.410 H and a capacitance of 0.250 nF . During the current oscillations, the maximum current in the inductor is 1.80 A . What is the maximum energy Emax stored in the capacitor at any time during the current oscillations? How many times per second does the capacitor contain the amount of energy found in part A? Please show all steps.arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning
An Introduction to Physical SciencePhysicsISBN:9781305079137Author:James Shipman, Jerry D. Wilson, Charles A. Higgins, Omar TorresPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





