Concept explainers
Videos
To write:
A menu-driven program to investigate the constant
Answer to Problem 29E
Solution:
The script file is,
clc
clear all
close all
% MATLAB code to calcualte the value of pi by different options.
%script file.
select = menu('select a option for pi', 'Machin''s formula', 'Leibniz''s formula:n-terms','Leibniz''s formula:good approximation','Exit');
%select the different options in menu.
while select == 0
disp('not valid! please choose one of the choices')
select = menu('select a option for pi', 'Machin''s formula', 'Leibniz''s formula:n-terms','Leibniz''s formula:good approximation','Exit');
end
end
% end of function
%The script file should be placed in the same folder.
The script file is,
% MATLAB code to calcualte the value of pi by Machinformula.
%script file.
function machinformula
pivalues = 4*(4*atan(1/5)-atan(1/239));
%define the variable pivalues.
fprintf('the value of pi using Machin''s formula is%.4f\n', pivalues)
%print the value of pi.
end
% end of function
%The script file should be placed in the same folder.
The script file is,
% MATLAB code to get the value of integer.
%script file.
function out = valuen
out = input('A positive integer for n is entered:');
%the value of positive integer is entered.
while out˜= int32(out)||out<=0
out = input('not valid! A posiytive integer for n is entered:');
end
end
% end of function
%The script file should be placed in the same folder.
The script file is,
% MATLAB code to calcualte the value of pi by leibniz's formula for the specific terms.
%script file.
function leibn
out = valuen;
numerat = -4.*cumprod(-ones(1, out));
%define the variable numerat as numerator.
denomina = 1:2:2*out;
%define the variable denomina as denominator.
pievalues = sum((numerat)./(denomina));
fprintf('the approximation of Leibniz for pi with %d terms is %.4f\n', out, pievalues);
%print the value of pi.
end
% end of function
%The script file should be placed in the same folder.
The script file is,
% MATLAB code to calcualte the value of pi by leibniz's formula till the good apprroxiamtion is found..
%script file
function leibgood
error = 0.01;
N = 1;
S = 2;
runsum = 0;
difference = 1;
while error < difference
term = (-1)^S*4/N;
temp = runsum;
runsum = runsum + term;
difference = abs(temp-runsum);
N = N+2;
S = S+1;
end
fprintf('An approximation of pi using Leibniz ''series within %.2f is %.2f\n', error, runsum)
%print the value of pi.
end
% end of function
%The script file should be placed in the same folder.
The main script file is,
% MATLAB code to calcualte the value of pi.
%script file.
select = -1;
while select ˜= 4
select = pivalues;
switch select
%select the different options to get the value of pi.
case 1
machinformula
case 2
leibn
case 3
leibgood
end
end
% end of function
%The script file should be placed in the same folder.
Explanation of Solution
Machin’s formula is given as,
Leibniz’s formula is given as,
The approximation till the fourth term is given as,
MATLAB Code:
% MATLAB code to calcualte the value of pi by different options.
%script file.
function select = pivalues
select = menu('select a option for pi', 'Machin''s formula', 'Leibniz''s formula:n-terms','Leibniz''s formula:good approximation','Exit');
%select the different options in menu.
while select == 0
disp('not valid! please choose one of the choices')
select = menu('select a option for pi', 'Machin''s formula', 'Leibniz''s formula:n-terms','Leibniz''s formula:good approximation','Exit');
end
end
% end of function
%The script file should be placed in the same folder.
% MATLAB code to calcualte the value of pi by Machinformula.
%script file.
function machinformula
pivalues = 4*(4*atan(1/5)-atan(1/239));
%define the variable pivalues.
fprintf('the value of pi using Machin''s formula is%.4f\n', pivalues)
%print the value of pi.
end
% end of function
%The script file should be placed in the same folder.
% MATLAB code to get the value of integer.
%script file.
function out = valuen
out = input('A positive integer for n is entered:');
%the value of positive integer is entered.
while out˜= int32(out)||out<=0
out = input('not valid! A posiytive integer for n is entered:');
end
end
% end of function
%The script file should be placed in the same folder.
% MATLAB code to calcualte the value of pi by leibniz's formula for the specific terms.
%script file.
function leibn
out = valuen;
numerat = -4.*cumprod(-ones(1, out));
%define the variable numerat as numerator.
denomina = 1:2:2*out;
%define the variable denomina as denominator.
pievalues = sum((numerat)./(denomina));
fprintf('the approximation of Leibniz for pi with %d terms is %.4f\n', out, pievalues);
%print the value of pi.
end
% end of function
%The script file should be placed in the same folder.
% MATLAB code to calcualte the value of pi by leibniz's formula till the good apprroxiamtion is found..
%script file
function leibgood
error = 0.01;
N = 1;
S = 2;
runsum = 0;
difference = 1;
while error < difference
term = (-1)^S*4/N;
temp = runsum;
runsum = runsum + term;
difference = abs(temp-runsum);
N = N+2;
S = S+1;
end
fprintf('An approximation of pi using Leibniz ''series within %.2f is %.2f\n', error, runsum)
%print the value of pi.
end
% end of function
%The script file should be placed in the same folder.
% MATLAB code to calcualte the value of pi.
%script file.
select = -1;
while select ˜= 4
select = pivalues;
switch select
%select the different options to get the value of pi.
case 1
machinformula
case 2
leibn
case 3
leibgood
end
end
% end of function
%The script file should be placed in the same folder.
Save the MATLAB scripts with names, pivalues.m, machinformula.m, valuen.m, leibn.m, leibgood.m and main.m in the current folder. Execute the script by typing the script name at the command window to generate result.
Result:
The results is,
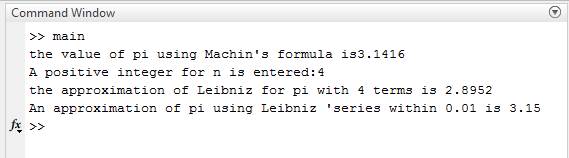
Therefore, the result and script files are stated above.
Want to see more full solutions like this?
Chapter 6 Solutions
MATLAB: A Practical Introduction to Programming and Problem Solving
- You have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step on excel Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple…arrow_forwardHere is data with as the response variable. x y54.4 19.124.9 99.334.5 9.476.6 0.359.4 4.554.4 0.139.2 56.354 15.773.8 9-156.1 319.2Make a scatter plot of this data. Which point is an outlier? Enter as an ordered pair, e.g., (x,y). (x,y)= Find the regression equation for the data set without the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_wo= Find the regression equation for the data set with the outlier. Enter the equation of the form mx+b rounded to three decimal places. y_w=arrow_forwardYou have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. please do it step by step Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear…arrow_forward
- Exercises: Find all the whole number solutions of the congruence equation. 1. 3x 8 mod 11 2. 2x+3= 8 mod 12 3. 3x+12= 7 mod 10 4. 4x+6= 5 mod 8 5. 5x+3= 8 mod 12arrow_forwardScenario Sales of products by color follow a peculiar, but predictable, pattern that determines how many units will sell in any given year. This pattern is shown below Product Color 1995 1996 1997 Red 28 42 21 1998 23 1999 29 2000 2001 2002 Unit Sales 2003 2004 15 8 4 2 1 2005 2006 discontinued Green 26 39 20 22 28 14 7 4 2 White 43 65 33 36 45 23 12 Brown 58 87 44 48 60 Yellow 37 56 28 31 Black 28 42 21 Orange 19 29 Purple Total 28 42 21 49 68 78 95 123 176 181 164 127 24 179 Questions A) Which color will sell the most units in 2007? B) Which color will sell the most units combined in the 2007 to 2009 period? Please show all your analysis, leave formulas in cells, and specify any assumptions you make.arrow_forwardOne hundred students were surveyed about their preference between dogs and cats. The following two-way table displays data for the sample of students who responded to the survey. Preference Male Female TOTAL Prefers dogs \[36\] \[20\] \[56\] Prefers cats \[10\] \[26\] \[36\] No preference \[2\] \[6\] \[8\] TOTAL \[48\] \[52\] \[100\] problem 1 Find the probability that a randomly selected student prefers dogs.Enter your answer as a fraction or decimal. \[P\left(\text{prefers dogs}\right)=\] Incorrect Check Hide explanation Preference Male Female TOTAL Prefers dogs \[\blueD{36}\] \[\blueD{20}\] \[\blueE{56}\] Prefers cats \[10\] \[26\] \[36\] No preference \[2\] \[6\] \[8\] TOTAL \[48\] \[52\] \[100\] There were \[\blueE{56}\] students in the sample who preferred dogs out of \[100\] total students.arrow_forward
- Business discussarrow_forwardYou have been hired as an intern to run analyses on the data and report the results back to Sarah; the five questions that Sarah needs you to address are given below. Does there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. (In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size). Include the manufacturer dummy variable (Samsung=1, 0 otherwise) and estimate the relationship between screen size, price and manufacturer dummy as a multiple linear regression model. Interpret the…arrow_forwardDoes there appear to be a positive or negative relationship between price and screen size? Use a scatter plot to examine the relationship. How to take snapshots: if you use a MacBook, press Command+ Shift+4 to take snapshots. If you are using Windows, use the Snipping Tool to take snapshots. Question 1: Determine and interpret the correlation coefficient between the two variables. In your interpretation, discuss the direction of the relationship (positive, negative, or zero relationship). Also discuss the strength of the relationship. Value of correlation coefficient: Direction of the relationship (positive, negative, or zero relationship): Strength of the relationship (strong/moderate/weak): Question 2: Estimate the relationship between screen size and price using a simple linear regression model and interpret the estimated coefficients. In your interpretation, tell the dollar amount by which price will change for each unit of increase in screen size. (The answer for the…arrow_forward
- In this problem, we consider a Brownian motion (W+) t≥0. We consider a stock model (St)t>0 given (under the measure P) by d.St 0.03 St dt + 0.2 St dwt, with So 2. We assume that the interest rate is r = 0.06. The purpose of this problem is to price an option on this stock (which we name cubic put). This option is European-type, with maturity 3 months (i.e. T = 0.25 years), and payoff given by F = (8-5)+ (a) Write the Stochastic Differential Equation satisfied by (St) under the risk-neutral measure Q. (You don't need to prove it, simply give the answer.) (b) Give the price of a regular European put on (St) with maturity 3 months and strike K = 2. (c) Let X = S. Find the Stochastic Differential Equation satisfied by the process (Xt) under the measure Q. (d) Find an explicit expression for X₁ = S3 under measure Q. (e) Using the results above, find the price of the cubic put option mentioned above. (f) Is the price in (e) the same as in question (b)? (Explain why.)arrow_forwardProblem 4. Margrabe formula and the Greeks (20 pts) In the homework, we determined the Margrabe formula for the price of an option allowing you to swap an x-stock for a y-stock at time T. For stocks with initial values xo, yo, common volatility σ and correlation p, the formula was given by Fo=yo (d+)-x0Þ(d_), where In (±² Ꭲ d+ õ√T and σ = σ√√√2(1 - p). дго (a) We want to determine a "Greek" for ỡ on the option: find a formula for θα (b) Is дго θα positive or negative? (c) We consider a situation in which the correlation p between the two stocks increases: what can you say about the price Fo? (d) Assume that yo< xo and p = 1. What is the price of the option?arrow_forwardWe consider a 4-dimensional stock price model given (under P) by dẴ₁ = µ· Xt dt + йt · ΣdŴt where (W) is an n-dimensional Brownian motion, π = (0.02, 0.01, -0.02, 0.05), 0.2 0 0 0 0.3 0.4 0 0 Σ= -0.1 -4a За 0 0.2 0.4 -0.1 0.2) and a E R. We assume that ☑0 = (1, 1, 1, 1) and that the interest rate on the market is r = 0.02. (a) Give a condition on a that would make stock #3 be the one with largest volatility. (b) Find the diversification coefficient for this portfolio as a function of a. (c) Determine the maximum diversification coefficient d that you could reach by varying the value of a? 2arrow_forward
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill