Numerical Methods For Engineers, 7 Ed
Numerical Methods For Engineers, 7 Ed
7th Edition
ISBN: 9789352602131
Author: Canale Chapra
Publisher: MCGRAW-HILL HIGHER EDUCATION
bartleby

Videos

Textbook Question
Book Icon
Chapter 6, Problem 23P

Determine the roots of the simultaneous nonlinear equations

( x − 4 ) 2 + ( y − 4 ) 2 = 5 x 2 + y 2 = 16

Use a graphical approach to obtain your initial guesses. Determine refined estimates with the two-equation Newton-Raphson method described in Sec. 6.6.2.

Expert Solution & Answer
Check Mark
To determine

To calculate: The root of the non-linear simultaneous equations,

(x−4)2+(y−4)2=5x2+y2=16

By the two-equation Newton-Raphson method and find the initial guess by the graphical method.

Answer to Problem 23P

Solution:

The root of the simultaneous non-linear equations y=x2+1 and y=2cosx:

For the initial root (1.8,3.6) is x=1.80583 and y=3.56917.

For the initial root (3.6,1.8) is x=3.56917 and y=1.80583.

Explanation of Solution

Given information:

The non-linear simultaneous equation,

(x−4)2+(y−4)2=5x2+y2=16

Formula used:

The Newton-Raphson formula for two non-linear equation is,

xi+1=xi−ui∂vi∂y−vi∂ui∂y∂ui∂x∂vi∂y−∂ui∂y∂vi∂xyi+1=yi−vi∂ui∂x−ui∂vi∂x∂ui∂x∂vi∂y−∂ui∂y∂vi∂x

Calculation:

Use MATLAB to draw the graph of the equations, (x−4)2+(y−4)2=5 and x2+y2=16 as below,

Code:

clear;clc;

%x-coordinates spacing is defined.

x =linspace(-10,10,100);

%first function is defined.

y1_1 =(- x.^2+8.*x -11).^(1/2)+4;

y1_2 =4-(- x.^2+8.*x -11).^(1/2);

%second function is defined.

y2_1 =(4- x).^(1/2).*(x +4).^(1/2);

y2_2 =-(4- x).^(1/2).*(x +4).^(1/2);

Y1 =[y1_1,y1_2];

Y2 =[y2_1,y2_2];

X =[x,x];

%Plot command is used to draw the two function.

plot(X,Y1,X,Y2)

legend('(x-4)^2 + (y-4)^2 = 5','x^2 + y^2 = 16')

xlabel('x')

ylabel('y')

Output:

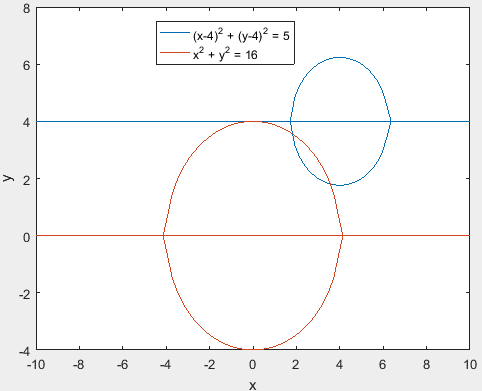
Numerical Methods For Engineers, 7 Ed, Chapter 6, Problem 23P

From the above graph, it is observed that there are two roots at (1.8,3.6) and (3.6,1.8).

Consider theequations,

(x−4)2+(y−4)2=5x2+y2=16

Rewrite the equation as below,

u(x,y)=5−(x−4)2−(y−4)2v(x,y)=16−x2−y2

Partial differentiate the above functions with respect to x,

∂u∂x=∂∂x[5−(x−4)2−(y−4)2]=∂∂x(5)−∂∂x[(x−4)2]−∂∂x[(y−4)2]=0−2(x−4)−0=−2x+8

And,

∂v∂x=∂∂x(16−x2−y2)=∂∂x(16)−∂∂x(x2)−∂∂x(y2)=0−2x−0=−2x

Now, partial differentiate the above functions with respect to y,

∂u∂y=∂∂y[5−(x−4)2−(y−4)2]=∂∂y(5)−∂∂y(x−4)2−∂∂y(y−4)2=0−0−2(y−4)=−2y+8

And,

∂v∂y=∂∂y(16−x2−y2)=∂∂y(16)−∂∂y(x2)−∂∂y(y2)=0−0−2y=−2y

Use initial guesses x0=1.8 and y0=3.6, the first iteration is,

x0+1=x0−u0∂v0∂y−v0∂u0∂y∂u0∂x∂v0∂y−∂u0∂y∂v0∂xx1=1.8−{5−((1.8)−4)2−((3.6)−4)2}(−2(3.6))−(16−(1.8)2−(3.6)2)(−2(3.6)+8)(−2(1.8)+8)(−2(3.6))−(−2(3.6)+8)(−2(1.8))=1.8−{5−(−2.2)2−(−0.4)2}(−7.2)−(16−3.24−12.96)(−7.2+8)(−3.6+8)(−7.2)−(−7.2+8)(−3.6)=1.8056

And,

y0+1=y0−v0∂u0∂x−u0∂v0∂x∂u0∂x∂v0∂y−∂u0∂y∂v0∂xy1=3.6−(16−(1.8)2−(3.6)2)(−2(1.8)+8)−{5−((1.8)−4)2−((3.6)−4)2}(−2(1.8))(−2(1.8)+8)(−2(3.6))−(−2(3.6)+8)(−2(1.8))=3.6−(16−3.24−12.96)(−3.6+8)−{5−(−2.2)2−(−0.4)2}(−3.6)(−3.6+8)(−7.2)−(−7.2+8)(−3.6)=3.5694

Now, use x1=1.8056 and y1=3.5694, the second iteration is,

x1+1=x1−u1∂v1∂y−v1∂u1∂y∂u1∂x∂v1∂y−∂u1∂y∂v1∂xx2=1.8056−{5−((1.8056)−4)2−((3.5694)−4)2}(−2(3.5694))−(16−(1.8056)2−(3.5694)2)(−2(3.5694)+8)(−2(1.8056)+8)(−2(3.5694))−(−2(3.5694)+8)(−2(1.8056))=1.8056−{−0.00081}(−7.14)−(−0.00081)(0.86)(4.389)(−7.14)−(0.86)(−3.6112)=1.80583

And,

y1+1=y1−v1∂u1∂x−u1∂v1∂x∂u1∂x∂v1∂y−∂u1∂y∂v1∂xy2=3.5694−(16−(1.8056)2−(3.5694)2)(−2(1.8056)+8)−{5−((1.8056)−4)2−((3.5694)−4)2}(−2(1.8056))(−2(1.8056)+8)(−2(3.5694))−(−2(3.5694)+8)(−2(1.8056))=3.5694−{−0.00081}(4.389)−(−0.00081)(−3.6112)(4.389)(−7.14)−(0.86)(−3.6112)=3.56917

Now, use x2=1.80583 and y2=3.56917, the third iteration is,

x2+1=x2−u2∂v2∂y−v2∂u2∂y∂u2∂x∂v2∂y−∂u2∂y∂v2∂xx3=1.80583−{5−((1.80583)−4)2−((3.56917)−4)2}(−2(3.56917))−(16−(1.80583)2−(3.56917)2)(−2(3.56917)+8)(−2(1.80583)+8)(−2(3.56917))−(−2(3.56917)+8)(−2(1.80583))=1.80583−{−0.0000035}(−7.13834)−(−0.0000035)(0.86166)(4.38834)(−7.13834)−(0.86166)(−3.61166)=1.80583

And,

y2+1=y2−v2∂u2∂x−u2∂v2∂x∂u2∂x∂v2∂y−∂u2∂y∂v2∂xy2=3.56917−(16−(1.80583)2−(3.56917)2)(−2(1.80583)+8)−{5−((1.80583)−4)2−((3.56917)−4)2}(−2(1.80583))(−2(1.80583)+8)(−2(3.56917))−(−2(3.56917)+8)(−2(1.80583))=3.56917−{−0.0000035}(4.38834)−(−0.0000035)(−3.61166)(4.38834)(−7.13834)−(0.86166)(−3.61166)=3.56917

Thus, all the iteration can be summarized as below,

i xi yi
0 1.8 3.6
1 1.8056 3.5694
2 1.80583 3.56917
3 1.80583 3.56917

Hence, the root of the simultaneous non-linear equations y=x2+1 and y=2cosx is x=1.80583 and y=3.56917.

Use initial guesses x0=3.6 and y0=1.8, the first iteration is,

x0+1=x0−u0∂v0∂y−v0∂u0∂y∂u0∂x∂v0∂y−∂u0∂y∂v0∂xx1=3.6−{5−((3.6)−4)2−((1.8)−4)2}(−2(1.8))−(16−(3.6)2−(1.8)2)(−2(1.8)+8)(−2(3.6)+8)(−2(1.8))−(−2(1.8)+8)(−2(3.6))=3.6−{0}(−3.6)−(−0.2)(4.4)(0.8)(−3.6)−(4.4)(−7.2)=3.56944

And,

y0+1=y0−v0∂u0∂x−u0∂v0∂x∂u0∂x∂v0∂y−∂u0∂y∂v0∂xy1=1.8−(16−(3.6)2−(1.8)2)(−2(3.6)+8)−{5−((3.6)−4)2−((1.8)−4)2}(−2(3.6))(−2(3.6)+8)(−2(1.8))−(−2(1.8)+8)(−2(3.6))=1.8−{−0.2}(0.8)−(0)(−7.2)(0.8)(−3.6)−(4.4)(−7.2)=1.80556

Now, use x1=3.56944 and y1=1.80556, the second iteration is,

x1+1=x1−u1∂v1∂y−v1∂u1∂y∂u1∂x∂v1∂y−∂u1∂y∂v1∂xx2=3.56944−{5−((3.56944)−4)2−((1.80556)−4)2}(−2(1.80556))−(16−(3.56944)2−(1.80556)2)(−2(1.80556)+8)(−2(3.56944)+8)(−2(1.80556))−(−2(1.80556)+8)(−2(3.56944))=3.56944−{−0.00095}(−3.61112)−(−0.00095)(4.38888)(0.86112)(−3.61112)−(4.38888)(−7.13888)=3.56917

And,

y1+1=y1−v1∂u1∂x−u1∂v1∂x∂u1∂x∂v1∂y−∂u1∂y∂v1∂xy2=1.80556−(16−(3.56944)2−(1.80556)2)(−2(3.56944)+8)−{5−((3.56944)−4)2−((1.80556)−4)2}(−2(3.56944))(−2(3.56944)+8)(−2(1.80556))−(−2(1.80556)+8)(−2(3.56944))=1.80556−{−0.00095}(0.86112)−(−0.00095)(−7.13888)(0.86112)(−3.61112)−(4.38888)(−7.13888)=1.80583

Now, use x2=3.56917 and y2=1.80583, the third iteration is,

x2+1=x2−u2∂v2∂y−v2∂u2∂y∂u2∂x∂v2∂y−∂u2∂y∂v2∂xx3=3.56917−{5−((3.56917)−4)2−((1.80583)−4)2}(−2(1.80583))−(16−(3.56917)2−(1.80583)2)(−2(1.80583)+8)(−2(3.56917)+8)(−2(1.80583))−(−2(1.80583)+8)(−2(3.56917))=3.56917−{−0.0000035}(−3.61166)−(−0.0000035)(4.38834)(0.86166)(−3.61166)−(4.38834)(−7.13834)=3.56917

And,

y2+1=y2−v2∂u2∂x−u2∂v2∂x∂u2∂x∂v2∂y−∂u2∂y∂v2∂xy2=1.80583−(16−(3.56917)2−(1.80583)2)(−2(3.56917)+8)−{5−((3.56917)−4)2−((1.80583)−4)2}(−2(3.56917))(−2(3.56917)+8)(−2(1.80583))−(−2(1.80583)+8)(−2(3.56917))=1.80583−{−0.0000035}(0.86166)−(−0.0000035)(−7.13834)(0.86166)(−3.61166)−(4.38834)(−7.13834)=1.80583

Thus, all the iteration can be summarized as below,

i xi yi
0 3.6 1.8
1 3.56944 1.80556
2 3.56917 1.80583
3 3.56917 1.80583

Hence, the root of the simultaneous non-linear equations y=x2+1 and y=2cosx is x=3.56917 and y=1.80583.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Previous
Chapter 6, Problem 22P
Next
Chapter 6, Problem 24P
Students have asked these similar questions
Prove that f: f →> R 16 One-to- one.
Use mathematical induction to prove the following statement: For all natural numbers n, 5 divides 6^n - 1 (show every step in detail)
Use mathematical induction to prove the following statement: For all natural numbers n, 5 divides 6^n - 1

Chapter 6 Solutions

Numerical Methods For Engineers, 7 Ed

Ch. 6 - 6.1 Use simple fixed-point iteration to locate the...Ch. 6 - 6.2 Determine the highest real root of...Ch. 6 - Use (a) fixed-point iteration and (b) the...Ch. 6 - Determine the real roots of f(x)=1+5.5x4x2+0.5x3:...Ch. 6 - 6.5 Employ the Newton-Raphson method to determine...Ch. 6 - Determine the lowest real root of...Ch. 6 - 6.7 Locate the first positive root of Where x...Ch. 6 - 6.8 Determine the real root of, with the modified...Ch. 6 - 6.9 Determine the highest real root of:...Ch. 6 - 6.10 Determine the lowest positive root...
Ch. 6 - 6.11 Use the Newton-Raphson method to find the...Ch. 6 - 6.12 Given Use a root location technique to...Ch. 6 - You must determine the root of the following...Ch. 6 - Use (a) the Newton-Raphson method and (b) the...Ch. 6 - 6.15 The “divide and average” method, an old-time...Ch. 6 - (a) Apply the Newton-Raphson method to the...Ch. 6 - 6.17 The polynomial has a real root between 15...Ch. 6 - Use the secant method on the circle function...Ch. 6 - You are designing a spherical tank (Fig. P6.19) to...Ch. 6 - 6.20 The Manning equation can be written for a...Ch. 6 - 6.21 The function has a double root at. Use (a)...Ch. 6 - 6.22 Determine the roots of the following...Ch. 6 - 6.23 Determine the roots of the simultaneous...Ch. 6 - Repeat Prob. 6.23 except determine the positive...Ch. 6 - A mass balance for a pollutant in a well-mixed...Ch. 6 - Fir Prob. 6.25, the root can be located with...Ch. 6 - 6.27 Develop a user-friendly program for the...Ch. 6 - Develop a user-friendly program for the secant...Ch. 6 - 6.29 Develop a user-friendly program for the...Ch. 6 - 6.30 Develop a user-friendly program for Brent’s...Ch. 6 - 6.31 Develop a user-friendly program for the...Ch. 6 - 6.32 Use the program you developed in Prob. 6.31...

Additional Math Textbook Solutions

Find more solutions based on key concepts
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...

College Algebra (Collegiate Math)

1. How much money is Joe earning when he’s 30?

Pathways To Math Literacy (looseleaf)

NOTE: Write your answers using interval notation when appropriate. CHECKING ANALYTIC SKILLS Fill in each blank ...

Graphical Approach To College Algebra

Find E(X) for each of the distributions given in Exercise 2.1-3.

Probability And Statistical Inference (10th Edition)

Subtract. Check each answer by adding. a. 12-9 b. 22-7 c. 35-35 d. 70-0

Prealgebra

1. How is a sample related to a population?

Elementary Statistics: Picturing the World (7th Edition)

Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
SEE MORE TEXTBOOKS
03a: Numerical Differentiation Review; Author: Jaisohn Kim;https://www.youtube.com/watch?v=IMYsqbV4CEg;License: Standard YouTube License, CC-BY