Chapter 6, Problem 1C

1.

To determine

Obtain the descriptive statistics for the given data.

Answer to Problem 1C

Descriptive statistics for the data is as follows:

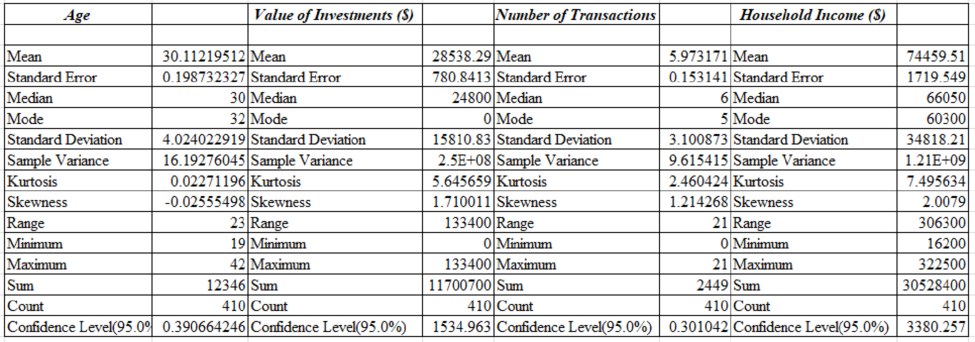
Explanation of Solution

Calculation:

The given information is about a young professional magazine. The magazine was successful in two years of publication. The magazine wants to expand the advertising base. The potential advertiser continually asks about the demographics and the interests of the subscribers to young professionals. The magazine conducts a survey to develop subscribers.

Software Procedure:

Step by step procedure to obtain the descriptive statistics using the Excel software:

• Enter the data in Excel spread sheet.
• Choose Data > Data Analysis > Descriptive Statistics.
• In Input range, select the columns of Age, Investment, Transactions, and Household income.
• Select Labels in first row check box and then select the output range.
• Select Summary statistics check box and confidence interval for Mean check box.
• Click OK.

Output using the Excel software is given below:

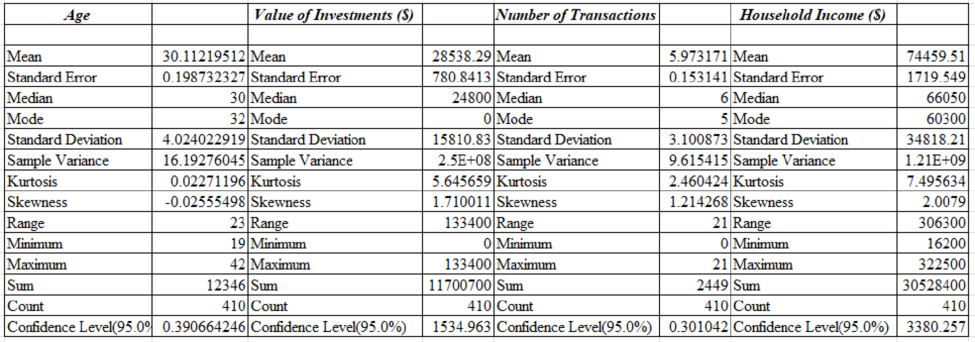
2.

To determine

Find the 95% confidence interval for the mean age and household income of subscribers.

Answer to Problem 1C

There is 95% confidence that the mean of the young professional subscribers of the age between 29.722 and 30.503 and there is 95% confidence that the mean of the young professional subscribers of the household income between $71,079 and $77,840.

Explanation of Solution

From the part (a) output, Mean and Margin of error for Age is 30.1122 and 0.3907. The mean and margin error for Household is 74459.51 and 3380.257.

The 95% confidence interval for the mean age is calculated as follows:

$\begin{array}{c}95\%\text{ CI}=\overline{x}\pm \text{Margin of error}\\ =30.1122\pm 0.3907\\ =\left(30.1122-0.3907,30.1122+0.3907\right)\\ =\left(29.722,30.503\right).\end{array}$

The 95% confidence interval for the mean household is calculated as follows:

$\begin{array}{c}95\%\text{ CI}=\overline{x}\pm \text{Margin of error}\\ =74459.51\pm 3380.257\\ =\left(74459.51-3380.257,74459.51+3380.257\right)\\ =\left(71079,77840\right).\end{array}$

Thus, there is 95% confidence that the mean of the young professional subscribers of the age between 29.722 and 30.503. There is 95% confidence that the mean of the young professional subscribers of the household income between $71,079 and $77,840.

3.

To determine

Find the 95% confidence interval for the proportion of the subscribers who have the broadband access at home and the proportion of the subscribers who have children.

Answer to Problem 1C

There is 95% confidence that the proportion of the young professional subscribers who have the broadband access between 57.75% and 67.14%.

There is 95% confidence that the proportion of the young professional subscribers who have children between 48.45% and 58.33%.

Explanation of Solution

The proportion of the young professional subscribers who have the broadband access:

Here 256 have access out of 410 subscribers.

$\begin{array}{c}\overline{p}=\frac{x}{n}\\ =\frac{256}{410}\\ =0.6244\end{array}$

Thus, the point estimate $\overline{p}$ is 0.6244

The proportion of the young professional subscribers who have children

Here 219 have children out of 410 subscribers.

$\begin{array}{c}\overline{p}=\frac{x}{n}\\ =\frac{219}{410}\\ =0.5341\end{array}$

Thus, the point estimate $\overline{p}$ is 0.5341

Here, the level of significance is 0.05.

The level of significance or probability for two-tailed is given as $\raisebox{1ex}{$\alpha $}\!\left/ \!\raisebox{-1ex}{$2$}\right.=\raisebox{1ex}{$0.05$}\!\left/ \!\raisebox{-1ex}{$2$}\right.=\mathrm{0.025.}$

The critical value is calculated by using the excel formula “=NORM.S.INV (probability)”.

Substitute the values in the excel formula: “=NORM.S.INV (0.025)”.

Thus the critical value is obtained as 1.96.

The 95% confidence that the proportion of the young professional subscribers who have the broadband access is given as:

 $\overline{p}\pm z_{\alpha /2}\sqrt{\frac{\overline{p}\times \left(1-\overline{p}\right)}{n}}$

$\begin{array}{l}0.6234\pm 1.96\sqrt{\frac{0.6234\times \left(1-0.6234\right)}{410}}\\ 0.6234\pm 0.046\end{array}$

$\begin{array}{l}0.6234-0.046<p<0.6234+0.046\\ 0.5774<p<0.6694\end{array}$

There is 95% confidence that the proportion of the young professional subscribers who have the broadband access between 57.75% and 67.14%.

The 95% confidence 95% confidence that the proportion of the young professional subscribers who have children is given as:

 $\overline{p}\pm z_{\alpha /2}\sqrt{\frac{\overline{p}\times \left(1-\overline{p}\right)}{n}}$

$\begin{array}{l}0.5341\pm 1.96\sqrt{\frac{0.5341\times \left(1-0.5341\right)}{410}}\\ 0.5341\pm 0.046\end{array}$

$\begin{array}{l}0.5341-0.048<p<0.5341+0.048\\ 0.4845<p<0.5833\end{array}$

There is 95% confidence that the proportion of the young professional subscribers who have children between 48.45% and 58.33%.

4.

To determine

Illustrate whether the young professionals are a good advertising outlet for online brokers or not. Justify with the statistical conclusion.

Answer to Problem 1C

The young professionals are the good advertising outlet for online brokers.

Explanation of Solution

From the results of Part 1, Most of the young professional subscribers have the financial investment for their home as $28,538. Some of them have the amount of investment like more than $100,000. So the mean number of transactions per year is nearly 6 per subscriber and some of the subscribers have mean number of transactions more than 6.

Since the large proportion has the broadband access that is 62.43%. It indicates that most of their subscribers likely to do business.

Thus, young professionals are the good advertising outlet for online brokers.

5.

To determine

Illustrate whether the magazine is good place for advertising companies, selling educational software, and computer games for young children.

Explanation of Solution

From the results of Part 1,

The mean age of subscribers is 30.112 years and 53.41% of the subscribers have children. The age of subscribers is reasonable to assume that their children are young age and then they can think that the young age children like about the educational software and the computer games.

Thus, it represents that the subscribers to young professional would be a good target for companies selling educational software and computer games for young children.

6.

To determine

Illustrate the types of articles that would be interested to readers of young professionals.

Explanation of Solution

By observing the results in Part 1, most of the young professionals are interested on the investment and for that the investment type of articles may be interested to the professionals. Also, the subscribers who have young children will be interested to read the parenting and child care types of articles.