Videos
(a)
Find which one is the biggest area among the two areas or check whether the two areas or equal or not.
(a)
Answer to Problem 19CAP
The area above the
Explanation of Solution
Calculation:
The given information is that the set of data is distributed normally with mean 3.5 and standard deviation 0.6.
Assume that the random variable X belongs to the set of the data.
The area below the mean is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score and make Decimals column as 4.
- Go to Data View, enter the value in score column as 3.5.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the
functions . - In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Scores from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
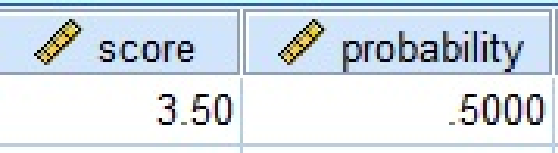
From the output, the value of
The area below the mean is 0.5000.
The area above the mean is,
The area above the mean is 0.5000.
Thus, the area above the mean and the area below the mean is same.
(b)
Find which one is the biggest area among the two areas or check whether the two areas or equal or not.
(b)
Answer to Problem 19CAP
The area between the value of 2.9 and 4.1 is higher than the area between the values of 3.5 and 4.7.
Explanation of Solution
Calculation:
The area between the values 2.9 and 4.1 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 4.1 and 2.9.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
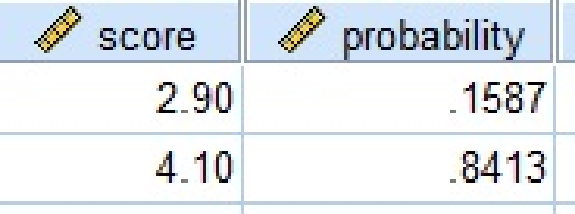
From the output, the value of
The area between the values of 2.9 and 4.1 is,
The area between the values of 2.9 and 4.1 is 0.6826.
The area between the values 3.5 and 4.7 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 3.5 and 4.7.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
From the output, the value of
The area between the values of 3.5 and 4.7 is,
The area between the values of 3.5 and 4.7 is 0.4772.
Thus, the area between the value of 2.9 and 4.1 is higher than the area between the values of 3.5 and 4.7.
(c)
Find which one is the biggest area among the two areas or check whether the two areas or equal or not.
(c)
Answer to Problem 19CAP
The area between the value mean and 3.5 is lower than the area above the value 5.3.
Explanation of Solution
Calculation:
The value of the mean is 3.5.
The area between the values mean and 3.5 is,
The area between the values of mean and 3.5 is 0.
The area above the value 5.3 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 5.3.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
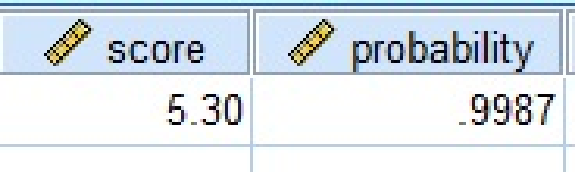
From the output, the value of
The area above 5.3 is,
The area above the value 5.3 is 0.0013.
Thus, the area between the value mean and 3.5 is lower than the area above the value 5.3.
(d)
Find which one is the biggest area among the two areas or check whether the two areas or equal or not.
(d)
Answer to Problem 19CAP
The area below 3.6 is equal to the area above 3.4.
Explanation of Solution
Calculation:
The area below 3.6 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 3.6.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
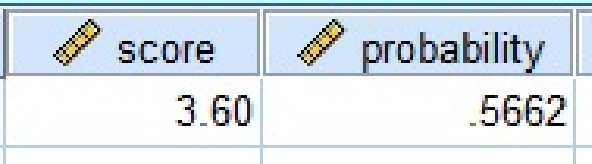
From the output, the value of
The area below 3.6 is 0.5662.
The area above 3.4 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 3.4.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
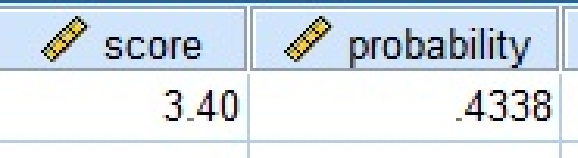
From the output, the value of
The area above 3.4 is,
The area above 3.4 is 0.5662.
Thus, the area below 3.6 is equal to the area above 3.4.
(e)
Find which one is the biggest area among the two areas or check whether the two areas or equal or not.
(e)
Answer to Problem 19CAP
The area between the 4.1 and 4.7 is lower than the area between the 2.9 and 3.5.
Explanation of Solution
Calculation:
The area between 4.1 and 4.7 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 4.1 and 4.7.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
From the output, the value of
The area between 4.1 and 4.7 is 0.1359.
The area between 2.9 and 3.5 is,
Software procedure:
Step by step procedure to obtain the probability by using SPSS software as follows:
- Go to Variable View, enter the variable name as Score.
- Go to Data View, enter the value in score column as 2.9 and 3.5.
- Go to Transform tab, choose Compute Variables.
- Enter Target variable as probabilty.
- Choose CDF &non-central CDF from the function group then select Cdf.Normal from the functions.
- In Numeric Expression CDF.NORMAL (pro, mean, stddev), choose the first variable as Score from the left side tab, enter second variable as 3.5 and third variable as 0.6.
- Click on OK.
Output using SPSS software is given as follows:
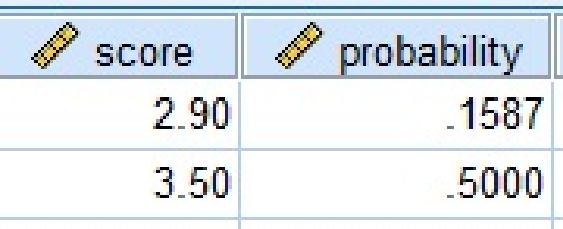
From the output, the value of
The area between 2.9 and 3.5 is 0.3413.
Thus, the area between the 4.1 and 4.7 is lower than the area between the 2.9 and 3.5.
Want to see more full solutions like this?
Chapter 6 Solutions
Statistics for the Behavioral Sciences
- 38. Possible values of X, the number of components in a system submitted for repair that must be replaced, are 1, 2, 3, and 4 with corresponding probabilities .15, .35, .35, and .15, respectively. a. Calculate E(X) and then E(5 - X).b. Would the repair facility be better off charging a flat fee of $75 or else the amount $[150/(5 - X)]? [Note: It is not generally true that E(c/Y) = c/E(Y).]arrow_forward74. The proportions of blood phenotypes in the U.S. popula- tion are as follows:A B AB O .40 .11 .04 .45 Assuming that the phenotypes of two randomly selected individuals are independent of one another, what is the probability that both phenotypes are O? What is the probability that the phenotypes of two randomly selected individuals match?arrow_forward53. A certain shop repairs both audio and video compo- nents. Let A denote the event that the next component brought in for repair is an audio component, and let B be the event that the next component is a compact disc player (so the event B is contained in A). Suppose that P(A) = .6 and P(B) = .05. What is P(BA)?arrow_forward
- 26. A certain system can experience three different types of defects. Let A;(i = 1,2,3) denote the event that the sys- tem has a defect of type i. Suppose thatP(A1) = .12 P(A) = .07 P(A) = .05P(A, U A2) = .13P(A, U A3) = .14P(A2 U A3) = .10P(A, A2 A3) = .011Rshelfa. What is the probability that the system does not havea type 1 defect?b. What is the probability that the system has both type 1 and type 2 defects?c. What is the probability that the system has both type 1 and type 2 defects but not a type 3 defect? d. What is the probability that the system has at most two of these defects?arrow_forwardThe following are suggested designs for group sequential studies. Using PROCSEQDESIGN, provide the following for the design O’Brien Fleming and Pocock.• The critical boundary values for each analysis of the data• The expected sample sizes at each interim analysisAssume the standardized Z score method for calculating boundaries.Investigators are evaluating the success rate of a novel drug for treating a certain type ofbacterial wound infection. Since no existing treatment exists, they have planned a one-armstudy. They wish to test whether the success rate of the drug is better than 50%, whichthey have defined as the null success rate. Preliminary testing has estimated the successrate of the drug at 55%. The investigators are eager to get the drug into production andwould like to plan for 9 interim analyses (10 analyzes in total) of the data. Assume thesignificance level is 5% and power is 90%.Besides, draw a combined boundary plot (OBF, POC, and HP)arrow_forwardPlease provide the solution for the attached image in detailed.arrow_forward
- 20 km, because GISS Worksheet 10 Jesse runs a small business selling and delivering mealie meal to the spaza shops. He charges a fixed rate of R80, 00 for delivery and then R15, 50 for each packet of mealle meal he delivers. The table below helps him to calculate what to charge his customers. 10 20 30 40 50 Packets of mealie meal (m) Total costs in Rands 80 235 390 545 700 855 (c) 10.1. Define the following terms: 10.1.1. Independent Variables 10.1.2. Dependent Variables 10.2. 10.3. 10.4. 10.5. Determine the independent and dependent variables. Are the variables in this scenario discrete or continuous values? Explain What shape do you expect the graph to be? Why? Draw a graph on the graph provided to represent the information in the table above. TOTAL COST OF PACKETS OF MEALIE MEAL 900 800 700 600 COST (R) 500 400 300 200 100 0 10 20 30 40 60 NUMBER OF PACKETS OF MEALIE MEALarrow_forwardLet X be a random variable with support SX = {−3, 0.5, 3, −2.5, 3.5}. Part ofits probability mass function (PMF) is given bypX(−3) = 0.15, pX(−2.5) = 0.3, pX(3) = 0.2, pX(3.5) = 0.15.(a) Find pX(0.5).(b) Find the cumulative distribution function (CDF), FX(x), of X.1(c) Sketch the graph of FX(x).arrow_forwardA well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forward
- 5. Let X and Y be independent random variables and let the superscripts denote symmetrization (recall Sect. 3.6). Show that (X + Y) X+ys.arrow_forward8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt