
To determine: The percentage change in
Introduction:
A bond refers to the debt securities issued by the governments or corporations for raising capital. The borrower does not return the face value until maturity. However, the investor receives the coupons every year until the date of maturity.
Bond price or bond value refers to the
Answer to Problem 16QP
The percentage change in bond price is as follows:
| Yield to maturity | Bond B | Bond T |
| 5% | 5.508% | 25.103% |
| 9% | (5.158%) | (18.40%) |
The interest rate risk is high for a bond with longer maturity, and the interest rate risk is low for a bond with shorter maturity period. The maturity period of Bond B is 3 years, and the maturity period of Bond T is 20 years. Hence, the Bond T’s bond price fluctuates higher than the bond price of Bond B due to longer maturity.
Explanation of Solution
Given information:
There are two bonds namely Bond B and Bond T. The coupon rate of both the bonds is 7 percent. The bonds pay the coupons semiannually. The price of the bond is equal to its par value. Assume that the par value of both the bonds is $1,000. Bond B will mature in 3 years, and Bond T will mature in 20 years.
Formula:
The formula to calculate the bond value:
Where,
“C” refers to the coupon paid per period
“F” refers to the face value paid at maturity
“r” refers to the yield to maturity
“t” refers to the periods to maturity
The formula to calculate the percentage change in price:
Determine the current price of Bond B:
Bond B is selling at par. It means that the bond value is equivalent to the face value. It also indicates that the coupon rate of the bond is equivalent to the yield to maturity of the bond. As the par value is $1,000, the bond value or bond price of Bond B will be $1,000.
Hence, the current price of Bond B is $1,000.
Determine the current yield to maturity on Bond B:
As the bond is selling at its face value, the coupon rate will be equal to the yield to maturity of the bond. The coupon rate of Bond B is 7 percent.
Hence, the yield to maturity of Bond B is 7 percent.
Determine the current price of Bond T:
Bond T is selling at par. It means that the bond value is equal to the face value. It also indicates that the coupon rate of the bond is equal to the yield to maturity of the bond. As the par value is $1,000, the bond value or bond price of Bond T will be $1,000.
Hence, the current price of Bond T is $1,000.
Determine the current yield to maturity on Bond T:
As the bond is selling at its face value, the coupon rate will be equal to the yield to maturity of the bond. The coupon rate of Bond T is 7 percent.
Hence, the yield to maturity of Bond T is 7 percent.
The percentage change in the bond value of Bond B and Bond T when the interest rates rise by 2 percent:
Compute the new interest rate (yield to maturity) when the interest rates rise:
The interest rate refers to the yield to maturity of the bond. The initial yield to maturity of the bonds is 7 percent. If the interest rates increases by 2 percent, then the new interest rate or yield to maturity will be 9 percent
Compute the bond value when the yield to maturity of Bond B rises to 9 percent:
The coupon rate of Bond B is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70
The yield to maturity is 9 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 4.5 percent
The remaining time to maturity is 3 years. As the coupon payment is semiannual, the semiannual periods to maturity are 6
Hence, the bond price of Bond B will be $948.42 when the interest rises to 9 percent.
Compute the percentage change in the price of Bond B when the interest rates rise to 9 percent:
The new price after the increase in interest rate is $948.42. The initial price of the bond was $1,000.
Hence, the percentage decrease in the price of Bond B is (5.158 percent) when the interest rates rise to 9 percent.
Compute the bond value when the yield to maturity of Bond T rises to 9 percent:
The coupon rate of Bond T is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70
The yield to maturity is 9 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 4.5 percent
The remaining time to maturity is 20 years. As the coupon payment is semiannual, the semiannual periods to maturity are 40
Hence, the bond price of Bond T will be $815.9841 when the interest rises to 9 percent.
Compute the percentage change in the price of Bond T when the interest rates rise to 9 percent:
The new price after the increase in interest rate is $815.9841. The initial price of the bond was $1,000.
Hence, the percentage decrease in the price of Bond T is (18.40 percent) when the interest rates rise to 9 percent.
The percentage change in the bond value of Bond B and Bond T when the interest rates decline by 2 percent:
Compute the new interest rate (yield to maturity) when the interest rates decline:
The interest rate refers to the yield to maturity of the bond. The initial yield to maturity of the bonds is 5 percent. If the interest rates decline by 2 percent, then the new interest rate or yield to maturity will be 5 percent
Compute the bond value when the yield to maturity of Bond B declines to 5 percent:
The coupon rate of Bond T is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70
The yield to maturity is 5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 2.5 percent
The remaining time to maturity is 3 years. As the coupon payment is semiannual, the semiannual periods to maturity are 6
Hence, the bond price of Bond B will be $1,055.08 when the interest declines to 5 percent.
Compute the percentage change in the price of Bond B when the interest rates decline to 5 percent:
The new price after the increase in interest rate is $1,055.08. The initial price of the bond was $1,000.
Hence, the percentage increase in the price of Bond B is 5.508 percent when the interest rates decline to 5 percent.
Compute the bond value when the yield to maturity of Bond T declines to 5 percent:
The coupon rate of Bond T is 7 percent, and its face value is $1,000. Hence, the annual coupon payment is $70
The yield to maturity is 5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 2.5 percent
The remaining time to maturity is 20 years. As the coupon payment is semiannual, the semiannual periods to maturity are 40
Hence, the bond price of Bond T will be $1,251.03 when the interest declines to 5 percent.
Compute the percentage change in the price of Bond T when the interest rates decline to 5 percent:
The new price after the increase in interest rate is $1,251.03. The initial price of the bond was $1,000.
Hence, the percentage increase in the price of Bond T is 25.103 percent when the interest rates decline to 5 percent.
A summary of the bond prices and yield to maturity of Bond B and Bond T:
Table 1
| Yield to maturity | Bond B | Bond T |
| 5% | $1,055.08 | $1,251.03 |
| 7% | $1,000.00 | $1,000.00 |
| 9% | $948.42 | $815.98 |
A graph indicating the relationship between bond prices and yield to maturity based on Table 1:
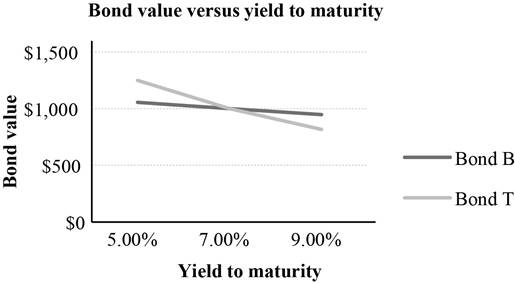
Interpretation of the graph:
The above graph indicates that the price fluctuation is higher in a bond with higher maturity. Bond T has a maturity period of 20 years. As its maturity period is longer, its price sensitivity to the interest rates is higher. Bond B has a maturity period of 3 years. As its maturity period is shorter, its price sensitivity to the interest rates is lower. Hence, a bond with longer maturity is subject to higher interest rate risk.
Want to see more full solutions like this?
Chapter 6 Solutions
ESSENTIAL OF CORP FINANCE W/CONNECT
- no ai do not answer this question if data is not clear or image is blurr. please comment i will write values . but do not amswer with unclear values. i will give unhelpful.arrow_forwardno ai Image is blurr do not answer this question if data is not clear or image is blurr. please comment i will write values but do not amswer with unclear values. i will give unhelpful sure.arrow_forwardDon't solve this question with unclear data. i will give unhelpful rating . please skip this qnarrow_forward
- The prodave paint company earned a net profit margin of 20% on revenues of $20m this year. Fixed Capital Investment was $2 m and depreciation was $3 m. Working capital Investment equals 7.5% of the Sales level in that year. Net income, fixed Capital Investment, depreciation, interest expenses and sales are expected to grow at 10% per year for the next 5 years. After 5 years, the growth in sales , net income, depreciation and interest expenses will decline to a stable 5% per year and fixed Capital Investment and depreciation will offset each other. The tax rate is 40% and the prodave has 1 m shares of common stock outstanding and long term debt paying 12.5% interest trading at it's par value of $32 m. The WACC is 17% during the high growth stage and 15% during the stable growth stage. Required: a) Calculate FCFE b) Determine FCFF c) Estimate the value of Equity d) Calculate the value of the Firmarrow_forwardA key dynamic within any Multi-National Corporation (MNC) is cash and foreign exchange risk exposure. Cash management is critical and also heavily influenced by global dynamics, especially since COVID-19. Within the Caribbean and North American jurisdiction, the economic framework is tightly connected with the major Asian economies of China, the United Kingdom and Japan. The Caribbean and the North American economy have been a barometer of the global economic cycle.) For both Caribbean and North American economies, many Multi-National Corporations have made significant investments to reduce the production cost of goods and diversification benefits. Despite the benefits that could materialize, some North American countries have not been resilient through Global market shocks. Given this context, the following questions require research within the Caribbean context and current market dynamics since COVID-19. Your Manager has asked you to address the following concerns in the report 1)…arrow_forwardA key dynamic within any Multi-National Corporation (MNC) is cash and foreign exchange risk exposure. Cash management is critical and also heavily influenced by global dynamics, especially since COVID-19. Within the Caribbean and North American jurisdiction, the economic framework is tightly connected with the major Asian economies of China, the United Kingdom and Japan. The Caribbean and the North American economy have been a barometer of the global economic cycle.) For both Caribbean and North American economies, many Multi-National Corporations have made significant investments to reduce the production cost of goods and diversification benefits. Despite the benefits that could materialize, some North American countries have not been resilient through Global market shocks. Given this context, the following questions require research within the Caribbean context and current market dynamics since COVID-19. Your Manager has asked you to address the following concerns in the report 1)…arrow_forward
- A key dynamic within any Multi-National Corporation (MNC) is cash and foreign exchange risk exposure. Cash management is critical and also heavily influenced by global dynamics, especially since COVID-19. Within the Caribbean and North American jurisdiction, the economic framework is tightly connected with the major Asian economies of China, the United Kingdom and Japan. The Caribbean and the North American economy have been a barometer of the global economic cycle.) For both Caribbean and North American economies, many Multi-National Corporations have made significant investments to reduce the production cost of goods and diversification benefits. Despite the benefits that could materialize, some North American countries have not been resilient through Global market shocks. Given this context, the following questions require research within the Caribbean context and current market dynamics since COVID-19. Your Manager has asked you to address the following concerns in the report 1)…arrow_forwardJeff Krause purchased 1,000 shares of a speculative stock in January for $1.89 per share. Six months later, he sold them for $9.95 per share. He uses an online broker that charges him $10.00 per trade. What was Jeff's annualized HPR on this investment? Jeff's annualized HPR on this investment is %. (Round to the nearest whole percent.)arrow_forwardCongratulations! Your portfolio returned 16.7% last year, 2.5% better than the market return of 14.2%. Your portfolio had a standard deviation of earnings equal to 18%, and the risk-free rate is equal to 4.4%. Calculate Sharpe's measure for your portfolio. If the market's Sharpe's measure is 0.29, did you do better or worse than the market from a risk/return perspective? The Sharpe's measure of your portfolio is (Round to two decimal places.)arrow_forward
- On January 1, 2020, Simon Love's portfolio of 15 common stocks had a market value of $258,000. At the end of May 2020, Simon sold one of the stocks, which had a beginning-of-year value of $26,900, for $31,400. He did not reinvest those or any other funds in the portfolio during the year. He received total dividends from stocks in his portfolio of $11,900 during the year. On December 31, 2020, Simon's portfolio had a market value of $246,000. Find the HPR on Simon's portfolio during the year ended December 31, 2020. (Measure the amount of withdrawn funds at their beginning-of-year value.) Simon's portfolio HPR during the year ended December 31, 2020, is %. (Round to two decimal places.)arrow_forwardChee Chew's portfolio has a beta of 1.27 and earned a return of 13.6% during the year just ended. The risk-free rate is currently 4.6%. The return on the market portfolio during the year just ended was 10.5%. a. Calculate Jensen's measure (Jensen's alpha) for Chee's portfolio for the year just ended. b. Compare the performance of Chee's portfolio found in part a to that of Carri Uhl's portfolio, which has a Jensen's measure of -0.25. Which portfolio performed better? Explain. c. Use your findings in part a to discuss the performance of Chee's portfolio during the period just ended.arrow_forwardDuring the year just ended, Anna Schultz's portfolio, which has a beta of 0.91, earned a return of 8.1%. The risk-free rate is currently 4.1%, and the return on the market portfolio during the year just ended was 9.4%. a. Calculate Treynor's measure for Anna's portfolio for the year just ended. b. Compare the performance of Anna's portfolio found in part a to that of Stacey Quant's portfolio, which has a Treynor's measure of 1.39%. Which portfolio performed better? Explain. c. Calculate Treynor's measure for the market portfolio for the year just ended. d. Use your findings in parts a and c to discuss the performance of Anna's portfolio relative to the market during the year just ended.arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





