Single Variable Calculus: Early Transcendentals, Volume I
8th Edition
ISBN: 9781305270343
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 6, Problem 12P
A cylindrical container of radius r and height L is partially filled with a liquid whose volume is V. If the container is rotated about its axis of symmetry with constant angular speed ω, then the container will induce a rotational motion in the liquid around the same axis. Eventually, the liquid will be rotating at the same angular speed as the container. The surface of the liquid will be convex, as indicated in the figure, because the centrifugal force on the liquid particles increases with the distance from the axis of the container. It can be shown that the surface of the liquid is a paraboloid of revolution generated by rotating the parabola
about the y-axis, where g is the acceleration due to gravity.
(a) Determine h as a function of ω.
(b) At what angular speed will the surface of the liquid touch the bottom? At what speed will it spill over the top?
(c) Suppose the radius of the container is 2 ft, the height is 7 ft, and the container and liquid are rotating at the same constant angular speed. The surface of the liquid is 5 ft below the top of the tank at the central axis and 4 ft below the top of the tank 1 ft out from the central axis.
(i) Determine the angular speed of the container and the volume of the fluid.
(ii) How far below the top of the tank is the liquid at the wall of the container?
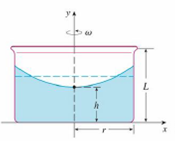
FIGURE FOR PROBLEM 12
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Find a plane containing the point (3, -3, 1) and the line of intersection of the planes 2x + 3y - 3z = 14
and -3x - y + z = −21.
The equation of the plane is:
Determine whether the lines
L₁ : F(t) = (−2, 3, −1)t + (0,2,-3) and
L2 : ƒ(s) = (2, −3, 1)s + (−10, 17, -8)
intersect. If they do, find the point of intersection.
● They intersect at the point
They are skew lines
They are parallel or equal
Answer questions 2
Chapter 6 Solutions
Single Variable Calculus: Early Transcendentals, Volume I
Ch. 6.1 - Find the area of the shaded region.Ch. 6.1 - Prob. 2ECh. 6.1 - Prob. 3ECh. 6.1 - Prob. 4ECh. 6.1 - Prob. 5ECh. 6.1 - Prob. 6ECh. 6.1 - Sketch the region enclosed by the given curves....Ch. 6.1 - Sketch the region enclosed by the given curves....Ch. 6.1 - Sketch the region enclosed by the given curves....Ch. 6.1 - Sketch the region enclosed by the given curves....
Ch. 6.1 - Prob. 11ECh. 6.1 - Prob. 12ECh. 6.1 - Prob. 13ECh. 6.1 - Prob. 14ECh. 6.1 - Prob. 15ECh. 6.1 - Prob. 16ECh. 6.1 - Prob. 17ECh. 6.1 - Prob. 18ECh. 6.1 - Prob. 19ECh. 6.1 - Sketch the region enclosed by the given curves and...Ch. 6.1 - Prob. 21ECh. 6.1 - Sketch the region enclosed by the given curves and...Ch. 6.1 - Prob. 23ECh. 6.1 - Prob. 24ECh. 6.1 - Prob. 25ECh. 6.1 - Sketch the region enclosed by the given curves and...Ch. 6.1 - Sketch the region enclosed by the given curves and...Ch. 6.1 - Prob. 28ECh. 6.1 - Prob. 29ECh. 6.1 - Prob. 30ECh. 6.1 - Prob. 31ECh. 6.1 - Prob. 32ECh. 6.1 - Use calculus to find the area of the triangle with...Ch. 6.1 - Use calculus to find the area of the triangle with...Ch. 6.1 - Prob. 35ECh. 6.1 - Evaluate the integral and interpret it as the area...Ch. 6.1 - Prob. 37ECh. 6.1 - Prob. 38ECh. 6.1 - Prob. 39ECh. 6.1 - Prob. 40ECh. 6.1 - Prob. 41ECh. 6.1 - Prob. 42ECh. 6.1 - Prob. 43ECh. 6.1 - Prob. 44ECh. 6.1 - Sketch the region in the xy-plane defined by the...Ch. 6.1 - Prob. 47ECh. 6.1 - The widths (in meters) of a kidney-shaped swimming...Ch. 6.1 - A cross-section of an airplane wing is shown....Ch. 6.1 - Prob. 50ECh. 6.1 - In Example 5, we modeled a measles pathogenesis...Ch. 6.1 - The rates at which rain fell, in inches per hour,...Ch. 6.1 - Two cars, A and B, start side by side and...Ch. 6.1 - Prob. 54ECh. 6.1 - Prob. 55ECh. 6.1 - Prob. 56ECh. 6.1 - Prob. 57ECh. 6.1 - Prob. 58ECh. 6.1 - Prob. 59ECh. 6.1 - Prob. 60ECh. 6.1 - Prob. 61ECh. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Prob. 2ECh. 6.2 - Prob. 3ECh. 6.2 - Prob. 4ECh. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Prob. 6ECh. 6.2 - Prob. 7ECh. 6.2 - Prob. 8ECh. 6.2 - Prob. 9ECh. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Prob. 13ECh. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Prob. 15ECh. 6.2 - Find the volume of the solid obtained by rotating...Ch. 6.2 - Prob. 17ECh. 6.2 - Prob. 18ECh. 6.2 - Refer to the figure and find the volume generated...Ch. 6.2 - Refer to the figure and find the volume generated...Ch. 6.2 - Refer to the figure and find the volume generated...Ch. 6.2 - Refer to the figure and find the volume generated...Ch. 6.2 - Prob. 23ECh. 6.2 - Prob. 24ECh. 6.2 - Prob. 25ECh. 6.2 - Prob. 26ECh. 6.2 - Prob. 27ECh. 6.2 - Prob. 28ECh. 6.2 - Prob. 29ECh. 6.2 - Prob. 30ECh. 6.2 - Prob. 31ECh. 6.2 - Prob. 32ECh. 6.2 - Set up an integral for the volume of the solid...Ch. 6.2 - Set up an integral for the volume of the solid...Ch. 6.2 - Prob. 35ECh. 6.2 - Prob. 36ECh. 6.2 - Prob. 39ECh. 6.2 - Prob. 40ECh. 6.2 - Each integral represents the volume of a solid....Ch. 6.2 - Prob. 42ECh. 6.2 - A CAT scan produces equally spaced cross-sectional...Ch. 6.2 - Prob. 44ECh. 6.2 - (a) If the region shown in the figure is rotated...Ch. 6.2 - Find the volume of the described solid S. A right...Ch. 6.2 - Prob. 48ECh. 6.2 - Find the volume of the described solid S. A cap of...Ch. 6.2 - Find the volume of the described solid S. A...Ch. 6.2 - Prob. 51ECh. 6.2 - Find the volume of the described solid S. A...Ch. 6.2 - Find the volume of the described solid S. A...Ch. 6.2 - Find the volume of the described solid S. The base...Ch. 6.2 - Prob. 55ECh. 6.2 - Find the volume of the described solid S. The base...Ch. 6.2 - Prob. 57ECh. 6.2 - Prob. 58ECh. 6.2 - Find the volume of the described solid S. The base...Ch. 6.2 - Prob. 60ECh. 6.2 - Prob. 61ECh. 6.2 - Prob. 62ECh. 6.2 - Prob. 63ECh. 6.2 - Prob. 64ECh. 6.2 - Prob. 65ECh. 6.2 - Find the volume common to two circular cylinders,...Ch. 6.2 - Prob. 67ECh. 6.2 - A bowl is shaped like a hemisphere with diameter...Ch. 6.2 - Prob. 69ECh. 6.2 - Prob. 70ECh. 6.2 - Some of the pioneers of calculus, such as Kepler...Ch. 6.2 - Prob. 72ECh. 6.3 - Let S be the solid obtained by rotating the region...Ch. 6.3 - Prob. 2ECh. 6.3 - Prob. 3ECh. 6.3 - Prob. 4ECh. 6.3 - Prob. 5ECh. 6.3 - Prob. 6ECh. 6.3 - Prob. 7ECh. 6.3 - Prob. 8ECh. 6.3 - Prob. 9ECh. 6.3 - Prob. 10ECh. 6.3 - Prob. 11ECh. 6.3 - Prob. 12ECh. 6.3 - Prob. 13ECh. 6.3 - Prob. 14ECh. 6.3 - Prob. 15ECh. 6.3 - Prob. 16ECh. 6.3 - Prob. 17ECh. 6.3 - Prob. 18ECh. 6.3 - Prob. 19ECh. 6.3 - Prob. 20ECh. 6.3 - Prob. 21ECh. 6.3 - Prob. 22ECh. 6.3 - (a) Set up an integral for the volume of the solid...Ch. 6.3 - Prob. 24ECh. 6.3 - Prob. 25ECh. 6.3 - Prob. 26ECh. 6.3 - Prob. 27ECh. 6.3 - If the region shown in the figure is rotated about...Ch. 6.3 - Prob. 29ECh. 6.3 - Prob. 30ECh. 6.3 - Prob. 31ECh. 6.3 - Prob. 32ECh. 6.3 - Prob. 33ECh. 6.3 - Prob. 34ECh. 6.3 - Prob. 37ECh. 6.3 - Prob. 38ECh. 6.3 - Prob. 39ECh. 6.3 - Prob. 40ECh. 6.3 - Prob. 41ECh. 6.3 - Prob. 42ECh. 6.3 - Prob. 43ECh. 6.3 - Prob. 44ECh. 6.3 - Prob. 45ECh. 6.3 - Prob. 46ECh. 6.3 - Prob. 47ECh. 6.3 - Use cylindrical shells to find the volume of the...Ch. 6.4 - A 360-lb gorilla climbs a tree to a height of 20...Ch. 6.4 - Prob. 2ECh. 6.4 - Prob. 3ECh. 6.4 - Prob. 4ECh. 6.4 - Prob. 5ECh. 6.4 - Prob. 6ECh. 6.4 - Prob. 7ECh. 6.4 - A spring has a natural length of 40 cm. If a 60-N...Ch. 6.4 - Suppose that 2 J of work is needed to stretch a...Ch. 6.4 - Prob. 10ECh. 6.4 - Prob. 11ECh. 6.4 - Prob. 12ECh. 6.4 - Show how to approximate the required work by a...Ch. 6.4 - Prob. 14ECh. 6.4 - Show how to approximate the required work by a...Ch. 6.4 - Prob. 16ECh. 6.4 - Prob. 17ECh. 6.4 - Prob. 18ECh. 6.4 - Prob. 19ECh. 6.4 - Prob. 20ECh. 6.4 - Show how to approximate the required work by a...Ch. 6.4 - Show how to approximate the required work by a...Ch. 6.4 - A tank is full of water. Find the work required to...Ch. 6.4 - A tank is full of water. Find the work required to...Ch. 6.4 - A tank is full of water. Find the work required to...Ch. 6.4 - A tank is full of water. Find the work required to...Ch. 6.4 - Suppose that for the tank in Exercise 23 the pump...Ch. 6.4 - Solve Exercise 24 if the tank is half full of oil...Ch. 6.4 - Prob. 29ECh. 6.4 - Prob. 30ECh. 6.4 - Prob. 31ECh. 6.4 - Prob. 32ECh. 6.4 - Prob. 33ECh. 6.4 - Prob. 34ECh. 6.5 - Prob. 1ECh. 6.5 - Prob. 2ECh. 6.5 - Find the average value of the function on the...Ch. 6.5 - Prob. 4ECh. 6.5 - Find the average value of the function on the...Ch. 6.5 - Prob. 6ECh. 6.5 - Prob. 7ECh. 6.5 - Find the average value of the function on the...Ch. 6.5 - Prob. 9ECh. 6.5 - Prob. 10ECh. 6.5 - Prob. 11ECh. 6.5 - (a) Find the average value of f on the given...Ch. 6.5 - Prob. 13ECh. 6.5 - Prob. 14ECh. 6.5 - Find the average value of f on [0, 8].Ch. 6.5 - The velocity graph of an accelerating car is...Ch. 6.5 - Prob. 17ECh. 6.5 - The velocity v of blood that flows in a blood...Ch. 6.5 - The linear density in a rod 8 m long is...Ch. 6.5 - (a) A cup of coffee has temperature 95C and takes...Ch. 6.5 - Prob. 21ECh. 6.5 - Prob. 22ECh. 6.5 - Prob. 23ECh. 6.5 - Use the diagram to show that if f is concave...Ch. 6.5 - Prob. 25ECh. 6.5 - Prob. 26ECh. 6 - (a) Draw two typical curves y = f(x) and y = g(x),...Ch. 6 - Prob. 2RCCCh. 6 - Prob. 3RCCCh. 6 - Prob. 4RCCCh. 6 - Prob. 5RCCCh. 6 - (a) What is the average value of a function f on...Ch. 6 - Prob. 1RECh. 6 - Prob. 2RECh. 6 - Prob. 3RECh. 6 - Prob. 4RECh. 6 - Find the area of the region bounded by the given...Ch. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Prob. 9RECh. 6 - Prob. 10RECh. 6 - Prob. 11RECh. 6 - Prob. 12RECh. 6 - Prob. 13RECh. 6 - Prob. 14RECh. 6 - Prob. 15RECh. 6 - Prob. 16RECh. 6 - Prob. 17RECh. 6 - Prob. 18RECh. 6 - Prob. 19RECh. 6 - Prob. 20RECh. 6 - Each integral represents the volume of a solid....Ch. 6 - Each integral represents the volume of a solid....Ch. 6 - Prob. 23RECh. 6 - Prob. 24RECh. 6 - The height of a monument is 20 m. A horizontal...Ch. 6 - Prob. 26RECh. 6 - Prob. 27RECh. 6 - Prob. 28RECh. 6 - Prob. 29RECh. 6 - A steel tank has the shape of a circular cylinder...Ch. 6 - Prob. 31RECh. 6 - Prob. 32RECh. 6 - Prob. 33RECh. 6 - Prob. 34RECh. 6 - (a) Find a positive continuous function f such...Ch. 6 - Prob. 2PCh. 6 - The figure shows a horizontal line y = c...Ch. 6 - A cylindrical glass of radius r and height L is...Ch. 6 - Prob. 5PCh. 6 - Prob. 6PCh. 6 - Prob. 7PCh. 6 - Prob. 8PCh. 6 - The figure shows a curve C with the property that,...Ch. 6 - Prob. 10PCh. 6 - Prob. 11PCh. 6 - A cylindrical container of radius r and height L...Ch. 6 - Prob. 13PCh. 6 - Prob. 15P
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Exercises 5-36, express all probabilities as fractions.
23. Combination Lock The typical combination lock us...
Elementary Statistics
Provide an example of a qualitative variable and an example of a quantitative variable.
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
Find all solutions of each equation in the interval .
Precalculus: A Unit Circle Approach (3rd Edition)
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
For Exercises 13–18, write the negation of the statement.
13. The cell phone is out of juice.
Math in Our World
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- How does a fourier transform works?arrow_forwardDetermine the radius of convergence of a power series:12.6.5, 12.6.6, 12.6.7, 12.6.8Hint: Use Theorem12.5.1 and root test, ratio test, integral testarrow_forwardCan you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forward
- Can you answer this question and give step by step and why and how to get it. Can you write it (numerical method)arrow_forwardThere are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three investment? STEP 1: The formula for compound interest is A = nt = P(1 + − − ) n², where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to A = Pert Find r and n for each model, and use these values to write A in terms of t for each case. Annual Model r=0.10 A = Y(t) = 1150 (1.10)* n = 1 Quarterly Model r = 0.10 n = 4 A = Q(t) = 1150(1.025) 4t Continuous Model r=0.10 A = C(t) =…arrow_forwardUse a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forward
- 5. For the function y-x³-3x²-1, use derivatives to: (a) determine the intervals of increase and decrease. (b) determine the local (relative) maxima and minima. (e) determine the intervals of concavity. (d) determine the points of inflection. (e) sketch the graph with the above information indicated on the graph.arrow_forwardCan you solve this 2 question numerical methodarrow_forward1. Estimate the area under the graph of f(x)-25-x from x=0 to x=5 using 5 approximating rectangles Using: (A) right endpoints. (B) left endpoints.arrow_forward
- 9. Use fundamental theorem of calculus to find the derivative d a) *dt sin(x) b)(x)√1-2 dtarrow_forward3. Evaluate the definite integral: a) √66x²+8dx b) x dx c) f*(2e* - 2)dx d) √√9-x² e) (2-5x)dx f) cos(x)dx 8)²₁₂√4-x2 h) f7dx i) f² 6xdx j) ²₂(4x+3)dxarrow_forward2. Consider the integral √(2x+1)dx (a) Find the Riemann sum for this integral using right endpoints and n-4. (b) Find the Riemann sum for this same integral, using left endpoints and n=4arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
01 - What Is an Integral in Calculus? Learn Calculus Integration and how to Solve Integrals.; Author: Math and Science;https://www.youtube.com/watch?v=BHRWArTFgTs;License: Standard YouTube License, CC-BY