Chapter 6, Problem 10REAE

Solution

To find: the indicated probability for a randomly selected x-value from the distribution using the standard normal table.

  $0.1841$

Given information:

The probability to be found is: $P\left(x\le 89\right)$

It is given that the distribution is normal and has mean $\overline{x}=95$ and standard deviation $\sigma =7$.

Concept Used:

Standard Normal Distribution

The standard normal distribution is the normal distribution with mean 0 and standard deviation1. The formula below can be used to transform x-values from a normal distribution with mean $\overline{x}$ and standard deviation $\sigma$ into z-values having a standard normal distribution.

  $z=\frac{x-\overline{x}}{\sigma }$

The z-value for a particular x-value is called the z-score for the x-value and is the number of standard deviations the x-value lies above or below the mean $\overline{x}$.

Standard Normal Table

If z is a randomly selected value from a standard normal distribution, the table below can be used to find the probability that z is less than or equal to some given value.

Standard Normal Table
z	.0	.1	.2	.3	.4	.5	.6	.7	.8	.9
-3	.0013	.0010	.0007	.0005	.0003	.0002	.0002	.0001	.0001	.0000+
-2	.0228	.0179	.0139	.0107	.0082	.0062	.0047	.0035	.0026	.0019
-1	.1587	.1357	.1151	.0968	.0808	.0668	.0548	.0446	.0359	.0287
-0	.5000	.4602	.4207	.3821	.3446	.3085	.2743	.2420	.2119	.1841
0	.5000	.5398	.5793	.6179	.6554	.6915	.7257	.7580	.7881	.8159
1	.8413	.8643	.8849	.9032	.9192	.9332	.9452	.9554	.9641	.9713
2	.9772	.9821	.9861	.9893	.9918	.9938	.9953	.9965	.9974	.9981
3	.9987	.9990	.9993	.9995	.9997	.9998	.9998	.9999	.9999	1.0000-

Explanation:

The objective is to find $P\left(x\le 89\right)$

First step is to find the z-score corresponding to the x-value of 89.

  $\begin{array}{c}z=\frac{x-\overline{x}}{\sigma }\\ =\frac{89-95}{7}\\ =\frac{-6}{7}\\ \approx -0.9\end{array}$

So,

  $P\left(x\le 89\right)\approx P\left(z\le -0.9\right)$

Now, to find this value, find the intersection point where row -0 and column .9 intersects.

  

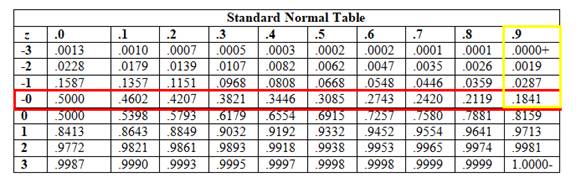
The table shows that:

  $P\left(z\le -0.9\right)=0.1841$

This means that:

  $P\left(x\le 89\right)\approx 0.1841$