CUSTOM BLITZER THINKING MATHEMATICALLY
CUSTOM BLITZER THINKING MATHEMATICALLY
7th Edition
ISBN: 9781323865040
Author: Blitzer
Publisher: PEARSON
bartleby

Concept explainers

Addition Rule of Probability
It simply refers to the likelihood of an event taking place whenever the occurrence of an event is uncertain. The probability of a single event can be calculated by dividing the number of successful trials of that event by the total number of trials.
Expected Value
When a large number of trials are performed for any random variable ‘X’, the predicted result is most likely the mean of all the outcomes for the random variable and it is known as expected value also known as expectation. The expected value, also known …
Probability Distributions
Understanding probability is necessary to know the probability distributions. In statistics, probability is how the uncertainty of an event is measured. This event can be anything. The most common examples include tossing a coin, rolling a die, or choosi…
Basic Probability
The simple definition of probability it is a chance of the occurrence of an event. It is defined in numerical form and the probability value is between 0 to 1. The probability value 0 indicates that there is no chance of that event occurring and the prob…
bartleby

Videos

Textbook Question
Book Icon
Chapter 5.5, Problem 51E

Shown in the figure is an 8-hour clock and the table for clock addition in the 8-hour clock system.

⊕ 0 1 2 3 4 5 6 7
0 0 1 2 3 4 5 6 7
1 1 2 3 4 5 6 7 0
2 2 3 4 5 6 7 0 1
3 3 4 5 6 7 0 1 2
4 4 5 6 7 0 1 2 3
5 5 6 7 0 1 2 3 4
6 6 7 0 1 2 3 4 5
7 7 0 1 2 3 4 5 6

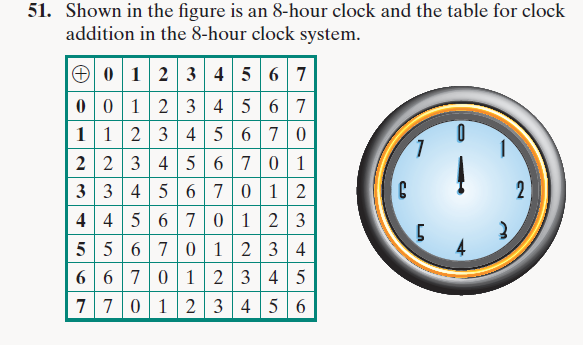
Chapter 5.5, Problem 51E, 51. Shown in the figure is an 8-hour clock and the table for clock addition in the 8-hour clock

a. How can you tell that the set {0, 1, 2, 3, 4, 5, 6, 7} is closed under the operation of clock addition?

b. Verify the associative property:

( 4 ⊕ 6 ) ⊕ 7   = 4 ⊕ ( 6 ⊕ 7 ) .

c. What is the identity element in the 8-hour clock system?

d. Find the inverse of each element in the 8-hour clock system.

e. Verify two cases of the commutative property:

5 ⊕ 6   = 6 ⊕ 5   and   4 ⊕ 7 = 7 ⊕ 4.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 5.5, Problem 50E
Next
Chapter 5.5, Problem 52E
Students have asked these similar questions
1 -1- Ο Graph of f y = + y = 1 + 1/2 ·2· x Graph of g y = 1- 플 The figure gives the graphs of the functions f and g in the xy-plane. The function of is given by f(x) = tan¹ x. Which of the following defines g(x)? A tan 1 x + 1 B - tan 1 x + П 2 C tan-1 (2/2) + 1 D tan-1 (2/2) + 1/1
In Problems 10-4, use the method of undetermined coefficients to determine the form of a particular solution for the given equation.
In Problems 10-40, use the method of undetermined coefficients to determine the form of a particular solution for the given equation. 2 1. y"" - 2y" - 5y/+6y= e² + x²

Chapter 5 Solutions

CUSTOM BLITZER THINKING MATHEMATICALLY

Ch. 5.1 - CHECK POINT 1 Which one of the following...Ch. 5.1 - Prob. 2CPCh. 5.1 - Prob. 3CPCh. 5.1 - CHECK POINT 4 A choral director needs to divide...Ch. 5.1 - CHECK POINT 5 Find the least common multiple of 18...Ch. 5.1 - CHECK POINT 6 A movie theater runs two documentary...Ch. 5.1 - 1. A natural number greater than 1 that has only...Ch. 5.1 - Fill in each blank so that the resulting statement...Ch. 5.1 - Prob. 3CVCCh. 5.1 - Prob. 4CVC
Ch. 5.1 - In Exercises 5-8, determine whether each statement...Ch. 5.1 - Prob. 6CVCCh. 5.1 - In Exercises 5-8, determine whether each statement...Ch. 5.1 - Prob. 8CVCCh. 5.1 - Use rules of divisibility to determine whether...Ch. 5.1 - Use rules of divisibility to determine whether...Ch. 5.1 - Prob. 3ECh. 5.1 - Use rules of divisibility to determine whether...Ch. 5.1 - Prob. 5ECh. 5.1 - Prob. 6ECh. 5.1 - Use rules of divisibility to determine whether...Ch. 5.1 - Prob. 8ECh. 5.1 - Use rules of divisibility to determine whether...Ch. 5.1 - Prob. 10ECh. 5.1 - In Exercises 11-24, use a calculator to determine...Ch. 5.1 - In Exercises 11-24, use a calculator to determine...Ch. 5.1 - Prob. 13ECh. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - Prob. 21ECh. 5.1 - Prob. 22ECh. 5.1 - Prob. 23ECh. 5.1 - Prob. 24ECh. 5.1 - Prob. 25ECh. 5.1 - Prob. 26ECh. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Prob. 36ECh. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Prob. 43ECh. 5.1 - Prob. 44ECh. 5.1 - Prob. 45ECh. 5.1 - Prob. 46ECh. 5.1 - Prob. 47ECh. 5.1 - Prob. 48ECh. 5.1 - Prob. 49ECh. 5.1 - Prob. 50ECh. 5.1 - Prob. 51ECh. 5.1 - In Exercises 45-56, find the greatest common...Ch. 5.1 - Prob. 53ECh. 5.1 - Prob. 54ECh. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - In Exercises 57-68, find the least common multiple...Ch. 5.1 - Prob. 59ECh. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - Prob. 64ECh. 5.1 - Prob. 65ECh. 5.1 - Prob. 66ECh. 5.1 - Prob. 67ECh. 5.1 - Prob. 68ECh. 5.1 - Prob. 69ECh. 5.1 - Prob. 70ECh. 5.1 - Prob. 71ECh. 5.1 - In Exercises 69-74, determine all values of d that...Ch. 5.1 - Prob. 73ECh. 5.1 - Prob. 74ECh. 5.1 - Prob. 75ECh. 5.1 - Prob. 76ECh. 5.1 - Prob. 77ECh. 5.1 - Prob. 78ECh. 5.1 - Prob. 79ECh. 5.1 - Prob. 80ECh. 5.1 - Prob. 81ECh. 5.1 - Prob. 82ECh. 5.1 - Prob. 83ECh. 5.1 - Prob. 84ECh. 5.1 - Prob. 85ECh. 5.1 - Prob. 86ECh. 5.1 - Prob. 87ECh. 5.1 - Prob. 88ECh. 5.1 - In Carl Sagan's novel Contact, Ellie Arroway, the...Ch. 5.1 - Prob. 90ECh. 5.1 - Prob. 91ECh. 5.1 - 92. A choral director needs to divide 180 men and...Ch. 5.1 - You have in front of you 310 five-dollar bills and...Ch. 5.1 - Prob. 94ECh. 5.1 - Prob. 95ECh. 5.1 - Prob. 96ECh. 5.1 - Two people are jogging around a circular track in...Ch. 5.1 - Prob. 98ECh. 5.1 - If a is a factor of c, what does this mea n?Ch. 5.1 - How do you know that 45 is divisible by 5?Ch. 5.1 - Prob. 101ECh. 5.1 - Prob. 102ECh. 5.1 - Prob. 103ECh. 5.1 - Prob. 104ECh. 5.1 - Prob. 105ECh. 5.1 - 106. What is the least common multiple of two or...Ch. 5.1 - Prob. 107ECh. 5.1 - Prob. 108ECh. 5.1 - Prob. 109ECh. 5.1 - Make Sense? In Exercises 110-113, determine...Ch. 5.1 - Make Sense? In Exercises 110-113, determine...Ch. 5.1 - Make Sense? In Exercises 110-113, determine...Ch. 5.1 - Prob. 113ECh. 5.1 - Prob. 114ECh. 5.1 - Prob. 115ECh. 5.1 - Prob. 116ECh. 5.1 - Prob. 117ECh. 5.1 - Prob. 118ECh. 5.1 - Prob. 119ECh. 5.1 - Prob. 120ECh. 5.1 - Prob. 121ECh. 5.1 - Prob. 122ECh. 5.1 - The following topics from number theory are...Ch. 5.1 - Prob. 124ECh. 5.1 - Prob. 125ECh. 5.1 - The following topics from number theory are...Ch. 5.1 - The following topics from number theory are...Ch. 5.1 - The following topics from number theory are...Ch. 5.2 - CHECKPOINT I Graph: a. − 4 b. 0 c. 3Ch. 5.2 - Prob. 2CPCh. 5.2 - CHECK POINT 3 Find the absolute value: a. | − 8 |...Ch. 5.2 - Prob. 4CPCh. 5.2 - Prob. 5CPCh. 5.2 - CHECK POINT 6 Evaluate: a. ( − 5 ) 2 b. − 5 2 c. (...Ch. 5.2 - Prob. 7CPCh. 5.2 - Prob. 8CPCh. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - 3. On a number line, the absolute value of a,...Ch. 5.2 - Fill in each blank so that the resulting statement...Ch. 5.2 - Prob. 5CVCCh. 5.2 - Prob. 6CVCCh. 5.2 - In Exercises 5-8, determine whether each statement...Ch. 5.2 - Prob. 8CVCCh. 5.2 - Prob. 1ECh. 5.2 - In Exercises 1-4, start by drawing a number line...Ch. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - In, Exercises 5-12, insert either < or > in the...Ch. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Prob. 15ECh. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Prob. 20ECh. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - Prob. 26ECh. 5.2 - Prob. 27ECh. 5.2 - Prob. 28ECh. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Prob. 33ECh. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - Prob. 43ECh. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Prob. 48ECh. 5.2 - Prob. 49ECh. 5.2 - Prob. 50ECh. 5.2 - Prob. 51ECh. 5.2 - Prob. 52ECh. 5.2 - Prob. 53ECh. 5.2 - Prob. 54ECh. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - Prob. 61ECh. 5.2 - Prob. 62ECh. 5.2 - Prob. 63ECh. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - Prob. 66ECh. 5.2 - Prob. 67ECh. 5.2 - Prob. 68ECh. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - Prob. 72ECh. 5.2 - Prob. 73ECh. 5.2 - Prob. 74ECh. 5.2 - Prob. 75ECh. 5.2 - Prob. 76ECh. 5.2 - Prob. 77ECh. 5.2 - Prob. 78ECh. 5.2 - Prob. 79ECh. 5.2 - Prob. 80ECh. 5.2 - In Exercises 81-100, use the order of operations...Ch. 5.2 - Prob. 82ECh. 5.2 - Prob. 83ECh. 5.2 - Prob. 84ECh. 5.2 - Prob. 85ECh. 5.2 - Prob. 86ECh. 5.2 - Prob. 87ECh. 5.2 - Prob. 88ECh. 5.2 - Prob. 89ECh. 5.2 - Prob. 90ECh. 5.2 - Prob. 91ECh. 5.2 - Prob. 92ECh. 5.2 - Prob. 93ECh. 5.2 - Prob. 94ECh. 5.2 - Prob. 95ECh. 5.2 - Prob. 96ECh. 5.2 - Prob. 97ECh. 5.2 - Prob. 98ECh. 5.2 - Prob. 99ECh. 5.2 - Prob. 100ECh. 5.2 - Prob. 101ECh. 5.2 - Prob. 102ECh. 5.2 - Prob. 103ECh. 5.2 - Prob. 104ECh. 5.2 - Prob. 105ECh. 5.2 - In Exercises 101-110, use the order of operations...Ch. 5.2 - Prob. 107ECh. 5.2 - Prob. 108ECh. 5.2 - Prob. 109ECh. 5.2 - Prob. 110ECh. 5.2 - In Exercises 111-114, express each sentence as a...Ch. 5.2 - In Exercises 111-114, express each sentence as a...Ch. 5.2 - Prob. 113ECh. 5.2 - Prob. 114ECh. 5.2 - Prob. 115ECh. 5.2 - Prob. 116ECh. 5.2 - Prob. 117ECh. 5.2 - Prob. 118ECh. 5.2 - Prob. 119ECh. 5.2 - Prob. 120ECh. 5.2 - Prob. 121ECh. 5.2 - Prob. 122ECh. 5.2 - Prob. 123ECh. 5.2 - Prob. 124ECh. 5.2 - Prob. 125ECh. 5.2 - Prob. 126ECh. 5.2 - The accompanying bar graph shows the amount of...Ch. 5.2 - Prob. 128ECh. 5.2 - Prob. 129ECh. 5.2 - Prob. 130ECh. 5.2 - Prob. 131ECh. 5.2 - Prob. 132ECh. 5.2 - Prob. 133ECh. 5.2 - Prob. 134ECh. 5.2 - Prob. 135ECh. 5.2 - Prob. 136ECh. 5.2 - Prob. 137ECh. 5.2 - Prob. 138ECh. 5.2 - Prob. 139ECh. 5.2 - Prob. 140ECh. 5.2 - Prob. 141ECh. 5.2 - Prob. 142ECh. 5.2 - Prob. 143ECh. 5.2 - Make Sense? In Exercises 144-147, determine...Ch. 5.2 - Make Sense? In Exercises 144-147, determine...Ch. 5.2 - Prob. 146ECh. 5.2 - Prob. 147ECh. 5.2 - Prob. 148ECh. 5.2 - Prob. 149ECh. 5.2 - Prob. 150ECh. 5.2 - Prob. 151ECh. 5.2 - Prob. 152ECh. 5.3 - CHECK POINT I Reduce 72 90 to lowest terms.Ch. 5.3 - CHECK POINT 2 Convert to an improper...Ch. 5.3 - Prob. 3CPCh. 5.3 - CHEAK POPINT 4 Express each rational number as a...Ch. 5.3 - Prob. 5CPCh. 5.3 - Prob. 6CPCh. 5.3 - CHECK POINT 7 Express as a quotient of...Ch. 5.3 - Prob. 8CPCh. 5.3 - Prob. 9CPCh. 5.3 - Prob. 10CPCh. 5.3 - CHECK POINT I I Find the sum: Ch. 5.3 - Prob. 12CPCh. 5.3 - Prob. 13CPCh. 5.3 - Prob. 14CPCh. 5.3 - Prob. 15CPCh. 5.3 - Prob. 1CVCCh. 5.3 - Prob. 2CVCCh. 5.3 - Prob. 3CVCCh. 5.3 - Prob. 4CVCCh. 5.3 - Prob. 5CVCCh. 5.3 - Prob. 6CVCCh. 5.3 - Prob. 7CVCCh. 5.3 - Prob. 8CVCCh. 5.3 - Prob. 1ECh. 5.3 - In Exercises 1-12, reduce each rational number to...Ch. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Prob. 12ECh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 16ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 19ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - In Exercises 25-36, express each rational number...Ch. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 44ECh. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - In Exercises 37-48, express each terminating...Ch. 5.3 - In Exercises 49-56, express each repeating decimal...Ch. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - In Exercises 49-56% express each repeating decimal...Ch. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - Prob. 60ECh. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 71ECh. 5.3 - Prob. 72ECh. 5.3 - Prob. 73ECh. 5.3 - Prob. 74ECh. 5.3 - Prob. 75ECh. 5.3 - Prob. 76ECh. 5.3 - Prob. 77ECh. 5.3 - Prob. 78ECh. 5.3 - Prob. 79ECh. 5.3 - In Exercises 57-104, perform the indicated...Ch. 5.3 - Prob. 81ECh. 5.3 - Prob. 82ECh. 5.3 - Prob. 83ECh. 5.3 - Prob. 84ECh. 5.3 - Prob. 85ECh. 5.3 - Prob. 86ECh. 5.3 - Prob. 87ECh. 5.3 - Prob. 88ECh. 5.3 - Prob. 89ECh. 5.3 - Prob. 90ECh. 5.3 - Prob. 91ECh. 5.3 - Prob. 92ECh. 5.3 - Prob. 93ECh. 5.3 - Prob. 94ECh. 5.3 - Prob. 95ECh. 5.3 - Prob. 96ECh. 5.3 - Prob. 97ECh. 5.3 - Prob. 98ECh. 5.3 - Prob. 99ECh. 5.3 - Prob. 100ECh. 5.3 - Prob. 101ECh. 5.3 - Prob. 102ECh. 5.3 - Prob. 103ECh. 5.3 - In Exercises 57-104, perform the indicated...Ch. 5.3 - Prob. 105ECh. 5.3 - Prob. 106ECh. 5.3 - Prob. 107ECh. 5.3 - Prob. 108ECh. 5.3 - Prob. 109ECh. 5.3 - Prob. 110ECh. 5.3 - Prob. 111ECh. 5.3 - Prob. 112ECh. 5.3 - Prob. 113ECh. 5.3 - Prob. 114ECh. 5.3 - Prob. 115ECh. 5.3 - Prob. 116ECh. 5.3 - Prob. 117ECh. 5.3 - Prob. 118ECh. 5.3 - Prob. 119ECh. 5.3 - Prob. 120ECh. 5.3 - Prob. 121ECh. 5.3 - Prob. 122ECh. 5.3 - Prob. 123ECh. 5.3 - Prob. 124ECh. 5.3 - Prob. 125ECh. 5.3 - Prob. 126ECh. 5.3 - Prob. 127ECh. 5.3 - Prob. 128ECh. 5.3 - Prob. 129ECh. 5.3 - Prob. 130ECh. 5.3 - A mix for eight servings of instant potatoes...Ch. 5.3 - Prob. 132ECh. 5.3 - Prob. 133ECh. 5.3 - Prob. 134ECh. 5.3 - Prob. 135ECh. 5.3 - Prob. 136ECh. 5.3 - Prob. 137ECh. 5.3 - Prob. 138ECh. 5.3 - Prob. 139ECh. 5.3 - Prob. 140ECh. 5.3 - Prob. 141ECh. 5.3 - Prob. 142ECh. 5.3 - 141. What is a rational number? Ch. 5.3 - Prob. 144ECh. 5.3 - Prob. 145ECh. 5.3 - Prob. 146ECh. 5.3 - Prob. 147ECh. 5.3 - Prob. 148ECh. 5.3 - Prob. 149ECh. 5.3 - 148. Explain how to multiply rational numbers. Use...Ch. 5.3 - Prob. 151ECh. 5.3 - Prob. 152ECh. 5.3 - ‘ What does it mean when we say that the set of...Ch. 5.3 - Make Sense? In Exercises 152-155, determine...Ch. 5.3 - Make Sense? In Exercises 152-155, determine...Ch. 5.3 - Prob. 156ECh. 5.3 - Prob. 157ECh. 5.3 - 156. Shown below is a short excerpt from “The...Ch. 5.3 - Prob. 159ECh. 5.3 - Prob. 160ECh. 5.3 - Prob. 161ECh. 5.3 - Prob. 162ECh. 5.4 - CHECK POINT I Simplify, if possible: a. b. c. Ch. 5.4 - CHECK POINT 2 Multiply: a. 3 ⋅ 10 b. 10 ⋅ 10 c. 6...Ch. 5.4 - Prob. 3CPCh. 5.4 - CHECK POINT 4 Add or subtract as indicated: a. 8 3...Ch. 5.4 - CHECK POINT 5 Add or subtract as indicated: a. b....Ch. 5.4 - Prob. 6CPCh. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - Hit in each blank so that the resulting statement...Ch. 5.4 - Prob. 3CVCCh. 5.4 - Prob. 4CVCCh. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - Prob. 6CVCCh. 5.4 - Fill in each blank so that the resulting statement...Ch. 5.4 - Prob. 8CVCCh. 5.4 - Prob. 9CVCCh. 5.4 - Prob. 10CVCCh. 5.4 - Prob. 1ECh. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - Evaluate each expression in Exercises 1-10. 100Ch. 5.4 - Prob. 7ECh. 5.4 - Prob. 8ECh. 5.4 - Prob. 9ECh. 5.4 - Prob. 10ECh. 5.4 - In Exercises 11-16, use a calculator with a square...Ch. 5.4 - In Exercises 11-16, use a calculator with a square...Ch. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Prob. 17ECh. 5.4 - In Exercises 17-24, simplify the square root. 50Ch. 5.4 - In Exercises 17-24, simplify the square root. 19....Ch. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.4 - In Exercises 17-24, simplify the square root. 23....Ch. 5.4 - Prob. 24ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - Prob. 30ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 32ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 34ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 36ECh. 5.4 - Prob. 37ECh. 5.4 - Prob. 38ECh. 5.4 - Prob. 39ECh. 5.4 - Prob. 40ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 42ECh. 5.4 - Prob. 43ECh. 5.4 - Prob. 44ECh. 5.4 - Prob. 45ECh. 5.4 - Prob. 46ECh. 5.4 - Prob. 47ECh. 5.4 - Prob. 48ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 50ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 52ECh. 5.4 - Prob. 53ECh. 5.4 - Prob. 54ECh. 5.4 - In Exercises 25-56, perform the indicated...Ch. 5.4 - Prob. 56ECh. 5.4 - Prob. 57ECh. 5.4 - Prob. 58ECh. 5.4 - In Exercises 57-66, rationalize the...Ch. 5.4 - Prob. 60ECh. 5.4 - Prob. 61ECh. 5.4 - Prob. 62ECh. 5.4 - In Exercises 57-66, rationalize the...Ch. 5.4 - Prob. 64ECh. 5.4 - In Exercises 57-66, rationalize the denominator. 2...Ch. 5.4 - Prob. 66ECh. 5.4 - In Exercises 67-74, perform the indicated...Ch. 5.4 - In Exercises 67-74, perform the indicated...Ch. 5.4 - Prob. 69ECh. 5.4 - Prob. 70ECh. 5.4 - Prob. 71ECh. 5.4 - Prob. 72ECh. 5.4 - Prob. 73ECh. 5.4 - Prob. 74ECh. 5.4 - Prob. 75ECh. 5.4 - Prob. 76ECh. 5.4 - Prob. 77ECh. 5.4 - Prob. 78ECh. 5.4 - Prob. 79ECh. 5.4 - Prob. 80ECh. 5.4 - Prob. 81ECh. 5.4 - Prob. 82ECh. 5.4 - Prob. 83ECh. 5.4 - Prob. 84ECh. 5.4 - Prob. 85ECh. 5.4 - Prob. 86ECh. 5.4 - Prob. 87ECh. 5.4 - Prob. 88ECh. 5.4 - Prob. 89ECh. 5.4 - 91. Explain how to add Ch. 5.4 - Prob. 91ECh. 5.4 - Prob. 92ECh. 5.4 - Prob. 93ECh. 5.4 - Prob. 94ECh. 5.4 - 97. I simplified and then I was able to perform...Ch. 5.4 - Using my calculator, I determined that 67=279,936,...Ch. 5.4 - Prob. 97ECh. 5.4 - Prob. 98ECh. 5.4 - Prob. 99ECh. 5.4 - Prob. 100ECh. 5.4 - Prob. 101ECh. 5.4 - Prob. 102ECh. 5.4 - Prob. 103ECh. 5.4 - Prob. 104ECh. 5.4 - Prob. 105ECh. 5.4 - Prob. 106ECh. 5.4 - Prob. 107ECh. 5.4 - Prob. 108ECh. 5.4 - The following topics related to irrational numbers...Ch. 5.4 - Prob. 110ECh. 5.4 - Prob. 111ECh. 5.4 - The following topics related to irrational numbers...Ch. 5.5 - Prob. 1CPCh. 5.5 - Prob. 2CPCh. 5.5 - Prob. 3CPCh. 5.5 - Prob. 4CPCh. 5.5 - Prob. 1CVCCh. 5.5 - Prob. 2CVCCh. 5.5 - Prob. 3CVCCh. 5.5 - Prob. 4CVCCh. 5.5 - Prob. 5CVCCh. 5.5 - Prob. 6CVCCh. 5.5 - The _________ property of multiplication states...Ch. 5.5 - 8. The product of a nonzero real number and its...Ch. 5.5 - Prob. 9CVCCh. 5.5 - Prob. 10CVCCh. 5.5 - Prob. 1ECh. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - Prob. 9ECh. 5.5 - 10. Give an example of a number that is a rational...Ch. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Prob. 22ECh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 25ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 35ECh. 5.5 - Prob. 36ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Prob. 39ECh. 5.5 - Prob. 40ECh. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 46ECh. 5.5 - Prob. 47ECh. 5.5 - Prob. 48ECh. 5.5 - Prob. 49ECh. 5.5 - Shown in the figure is a 7-hour clock and the...Ch. 5.5 - 51. Shown in the figure is an 8-hour clock and the...Ch. 5.5 - Prob. 52ECh. 5.5 - Prob. 53ECh. 5.5 - Prob. 54ECh. 5.5 - Prob. 55ECh. 5.5 - Prob. 56ECh. 5.5 - Prob. 57ECh. 5.5 - Prob. 58ECh. 5.5 - Prob. 59ECh. 5.5 - Prob. 60ECh. 5.5 - Prob. 61ECh. 5.5 - Prob. 62ECh. 5.5 - Prob. 63ECh. 5.5 - Prob. 64ECh. 5.5 - Prob. 65ECh. 5.5 - 66. a. b. c. Draw a conclusion about one of the...Ch. 5.5 - Prob. 67ECh. 5.5 - Prob. 68ECh. 5.5 - Prob. 69ECh. 5.5 - Prob. 70ECh. 5.5 - Prob. 71ECh. 5.5 - Prob. 72ECh. 5.5 - Prob. 73ECh. 5.5 - Prob. 74ECh. 5.5 - Prob. 75ECh. 5.5 - Prob. 76ECh. 5.5 - Prob. 77ECh. 5.5 - Prob. 78ECh. 5.5 - Prob. 79ECh. 5.5 - 80. What does it mean if we say that a set is...Ch. 5.5 - Prob. 81ECh. 5.5 - Prob. 82ECh. 5.5 - Prob. 83ECh. 5.5 - Prob. 84ECh. 5.5 - Prob. 85ECh. 5.5 - Prob. 86ECh. 5.5 - Prob. 87ECh. 5.5 - Prob. 88ECh. 5.5 - Prob. 89ECh. 5.5 - Prob. 90ECh. 5.5 - Prob. 91ECh. 5.5 - Prob. 92ECh. 5.5 - Prob. 93ECh. 5.5 - Prob. 94ECh. 5.5 - Prob. 95ECh. 5.5 - Prob. 96ECh. 5.5 - Prob. 97ECh. 5.5 - In Exercises 92-99, determine whether each...Ch. 5.5 - In Exercises 92-99, determine whether each...Ch. 5.6 - CHECK POINT I Use the zero exponent rule to...Ch. 5.6 - CHECK. POIN 2 Use the negative exponent rule to...Ch. 5.6 - CHECK POINT 3 Write each number in decimal...Ch. 5.6 - Prob. 4CPCh. 5.6 - Prob. 5CPCh. 5.6 - Prob. 6CPCh. 5.6 - Prob. 7CPCh. 5.6 - Prob. 8CPCh. 5.6 - Prob. 9CPCh. 5.6 - Prob. 1CVCCh. 5.6 - Prob. 2CVCCh. 5.6 - Prob. 3CVCCh. 5.6 - Prob. 4CVCCh. 5.6 - Prob. 5CVCCh. 5.6 - Prob. 6CVCCh. 5.6 - Prob. 7CVCCh. 5.6 - Prob. 8CVCCh. 5.6 - Prob. 9CVCCh. 5.6 - In Exercises 6-10, determine whether each...Ch. 5.6 - Prob. 1ECh. 5.6 - In Exercises 1-12, use properties of exponents to...Ch. 5.6 - Prob. 3ECh. 5.6 - Prob. 4ECh. 5.6 - Prob. 5ECh. 5.6 - Prob. 6ECh. 5.6 - Prob. 7ECh. 5.6 - Prob. 8ECh. 5.6 - Prob. 9ECh. 5.6 - Prob. 10ECh. 5.6 - Prob. 11ECh. 5.6 - Prob. 12ECh. 5.6 - Prob. 13ECh. 5.6 - Prob. 14ECh. 5.6 - In Exercises 13-24, use the zero and negative...Ch. 5.6 - Prob. 16ECh. 5.6 - In Exercises 13-24, use the zero and negative...Ch. 5.6 - Prob. 18ECh. 5.6 - Prob. 19ECh. 5.6 - Prob. 20ECh. 5.6 - Prob. 21ECh. 5.6 - Prob. 22ECh. 5.6 - Prob. 23ECh. 5.6 - Prob. 24ECh. 5.6 - Prob. 25ECh. 5.6 - Prob. 26ECh. 5.6 - Prob. 27ECh. 5.6 - Prob. 28ECh. 5.6 - In Exercises 25-30, use properties of exponents to...Ch. 5.6 - Prob. 30ECh. 5.6 - Prob. 31ECh. 5.6 - Prob. 32ECh. 5.6 - In Exercises 31-42, use properties of exponents to...Ch. 5.6 - Prob. 34ECh. 5.6 - In Exercises 31-42, use properties of exponents to...Ch. 5.6 - Prob. 36ECh. 5.6 - Prob. 37ECh. 5.6 - Prob. 38ECh. 5.6 - In Exercises 31—42, use properties of exponents to...Ch. 5.6 - Prob. 40ECh. 5.6 - In Exercises 31-42, use properties of exponents to...Ch. 5.6 - Prob. 42ECh. 5.6 - In Exercises 43-58, express each number in decimal...Ch. 5.6 - Prob. 44ECh. 5.6 - In Exercises 43-58, express each number in decimal...Ch. 5.6 - Prob. 46ECh. 5.6 - Prob. 47ECh. 5.6 - Prob. 48ECh. 5.6 - Prob. 49ECh. 5.6 - Prob. 50ECh. 5.6 - Prob. 51ECh. 5.6 - Prob. 52ECh. 5.6 - Prob. 53ECh. 5.6 - Prob. 54ECh. 5.6 - In Exercises 43-58, express each number in decimal...Ch. 5.6 - Prob. 56ECh. 5.6 - Prob. 57ECh. 5.6 - Prob. 58ECh. 5.6 - Prob. 59ECh. 5.6 - Prob. 60ECh. 5.6 - Prob. 61ECh. 5.6 - Prob. 62ECh. 5.6 - Prob. 63ECh. 5.6 - Prob. 64ECh. 5.6 - Prob. 65ECh. 5.6 - Prob. 66ECh. 5.6 - In Exercises 59-78, express each number in...Ch. 5.6 - Prob. 68ECh. 5.6 - Prob. 69ECh. 5.6 - Prob. 70ECh. 5.6 - Prob. 71ECh. 5.6 - Prob. 72ECh. 5.6 - In Exercises 59-78, express each number in...Ch. 5.6 - Prob. 74ECh. 5.6 - Prob. 75ECh. 5.6 - Prob. 76ECh. 5.6 - In Exercises 59-78, express each number in...Ch. 5.6 - Prob. 78ECh. 5.6 - In Exercises 79-92, perform the indicated...Ch. 5.6 - Prob. 80ECh. 5.6 - Prob. 81ECh. 5.6 - Prob. 82ECh. 5.6 - Prob. 83ECh. 5.6 - Prob. 84ECh. 5.6 - In Exercises 79-92, perform (he indicated...Ch. 5.6 - Prob. 86ECh. 5.6 - Prob. 87ECh. 5.6 - Prob. 88ECh. 5.6 - Prob. 89ECh. 5.6 - Prob. 90ECh. 5.6 - 91. Ch. 5.6 - Prob. 92ECh. 5.6 - Prob. 93ECh. 5.6 - In Exercises 93-102, perform the indicated...Ch. 5.6 - Prob. 95ECh. 5.6 - In Exercises 93-102, perform the indicated...Ch. 5.6 - In Exercises 93-102, perform the indicated...Ch. 5.6 - Prob. 98ECh. 5.6 - Prob. 99ECh. 5.6 - Prob. 100ECh. 5.6 - Prob. 101ECh. 5.6 - Prob. 102ECh. 5.6 - Prob. 103ECh. 5.6 - Prob. 104ECh. 5.6 - Prob. 105ECh. 5.6 - Prob. 106ECh. 5.6 - Prob. 107ECh. 5.6 - Prob. 108ECh. 5.6 - Prob. 109ECh. 5.6 - Prob. 110ECh. 5.6 - 111. a. In 2015, the United States government...Ch. 5.6 - Prob. 112ECh. 5.6 - We have seen that the 2016 U.S. national debt was...Ch. 5.6 - Prob. 114ECh. 5.6 - Prob. 115ECh. 5.6 - Prob. 116ECh. 5.6 - Prob. 117ECh. 5.6 - Prob. 118ECh. 5.6 - Prob. 119ECh. 5.6 - Prob. 120ECh. 5.6 - Prob. 121ECh. 5.6 - Prob. 122ECh. 5.6 - Prob. 123ECh. 5.6 - Prob. 124ECh. 5.6 - Prob. 125ECh. 5.6 - Prob. 126ECh. 5.6 - Prob. 127ECh. 5.6 - Prob. 128ECh. 5.6 - Prob. 129ECh. 5.6 - Prob. 130ECh. 5.6 - Prob. 131ECh. 5.6 - Prob. 132ECh. 5.6 - Prob. 133ECh. 5.6 - Prob. 134ECh. 5.6 - Prob. 135ECh. 5.6 - Prob. 136ECh. 5.6 - Prob. 137ECh. 5.6 - Prob. 138ECh. 5.6 - Prob. 139ECh. 5.6 - Prob. 140ECh. 5.6 - Prob. 141ECh. 5.6 - 142. The mad Dr. Frankenstein has gathered enough...Ch. 5.6 - Prob. 143ECh. 5.6 - Prob. 144ECh. 5.6 - Prob. 145ECh. 5.6 - Prob. 146ECh. 5.6 - Prob. 147ECh. 5.6 - Prob. 148ECh. 5.7 - Prob. 1CPCh. 5.7 - Prob. 2CPCh. 5.7 - Prob. 3CPCh. 5.7 - Prob. 4CPCh. 5.7 - Prob. 5CPCh. 5.7 - Prob. 6CPCh. 5.7 - CHECK POINT 7 Write the general term for the...Ch. 5.7 - Prob. 1CVCCh. 5.7 - Prob. 2CVCCh. 5.7 - Prob. 3CVCCh. 5.7 - Prob. 4CVCCh. 5.7 - In Exercises 1-20, write the first six terms of...Ch. 5.7 - In Exercises 1-20, write the first six terms of...Ch. 5.7 - In Exercises 1-20, write the first six terms of...Ch. 5.7 - In Exercises 1-20, write the first six terms of...Ch. 5.7 - In Exercises 1-20, write the first six terms of...Ch. 5.7 - Prob. 6ECh. 5.7 - Prob. 7ECh. 5.7 - Prob. 8ECh. 5.7 - Prob. 9ECh. 5.7 - Prob. 10ECh. 5.7 - Prob. 11ECh. 5.7 - Prob. 12ECh. 5.7 - Prob. 13ECh. 5.7 - Prob. 14ECh. 5.7 - Prob. 15ECh. 5.7 - Prob. 16ECh. 5.7 - Prob. 17ECh. 5.7 - Prob. 18ECh. 5.7 - Prob. 19ECh. 5.7 - Prob. 20ECh. 5.7 - Prob. 21ECh. 5.7 - Prob. 22ECh. 5.7 - Prob. 23ECh. 5.7 - Prob. 24ECh. 5.7 - Prob. 25ECh. 5.7 - Prob. 26ECh. 5.7 - Prob. 27ECh. 5.7 - Prob. 28ECh. 5.7 - Prob. 29ECh. 5.7 - Prob. 30ECh. 5.7 - Prob. 31ECh. 5.7 - Prob. 32ECh. 5.7 - Prob. 33ECh. 5.7 - Prob. 34ECh. 5.7 - Prob. 35ECh. 5.7 - Prob. 36ECh. 5.7 - Prob. 37ECh. 5.7 - Prob. 38ECh. 5.7 - Prob. 39ECh. 5.7 - Prob. 40ECh. 5.7 - Prob. 41ECh. 5.7 - Prob. 42ECh. 5.7 - Prob. 43ECh. 5.7 - Prob. 44ECh. 5.7 - Prob. 45ECh. 5.7 - Prob. 46ECh. 5.7 - Prob. 47ECh. 5.7 - Prob. 48ECh. 5.7 - Prob. 49ECh. 5.7 - Prob. 50ECh. 5.7 - Prob. 51ECh. 5.7 - Prob. 52ECh. 5.7 - Prob. 53ECh. 5.7 - Prob. 54ECh. 5.7 - Prob. 55ECh. 5.7 - In Exercises 49-70, write the first six terms of...Ch. 5.7 - Prob. 57ECh. 5.7 - Prob. 58ECh. 5.7 - Prob. 59ECh. 5.7 - Prob. 60ECh. 5.7 - Prob. 61ECh. 5.7 - Prob. 62ECh. 5.7 - Prob. 63ECh. 5.7 - Prob. 64ECh. 5.7 - Prob. 65ECh. 5.7 - Prob. 66ECh. 5.7 - Prob. 67ECh. 5.7 - Prob. 68ECh. 5.7 - Prob. 69ECh. 5.7 - Prob. 70ECh. 5.7 - Prob. 71ECh. 5.7 - Prob. 72ECh. 5.7 - Prob. 73ECh. 5.7 - Prob. 74ECh. 5.7 - Prob. 75ECh. 5.7 - Prob. 76ECh. 5.7 - Prob. 77ECh. 5.7 - Prob. 78ECh. 5.7 - Prob. 79ECh. 5.7 - Prob. 80ECh. 5.7 - Prob. 81ECh. 5.7 - Prob. 82ECh. 5.7 - Prob. 83ECh. 5.7 - Prob. 84ECh. 5.7 - Prob. 85ECh. 5.7 - Prob. 86ECh. 5.7 - Prob. 87ECh. 5.7 - In Exercises 71-90, find the indicated term for...Ch. 5.7 - Prob. 89ECh. 5.7 - Prob. 90ECh. 5.7 - Prob. 91ECh. 5.7 - Prob. 92ECh. 5.7 - Prob. 93ECh. 5.7 - Prob. 94ECh. 5.7 - Prob. 95ECh. 5.7 - Prob. 96ECh. 5.7 - Prob. 97ECh. 5.7 - Prob. 98ECh. 5.7 - Prob. 99ECh. 5.7 - Prob. 100ECh. 5.7 - Prob. 101ECh. 5.7 - Prob. 102ECh. 5.7 - Prob. 103ECh. 5.7 - Prob. 104ECh. 5.7 - Prob. 105ECh. 5.7 - Prob. 106ECh. 5.7 - Prob. 107ECh. 5.7 - Prob. 108ECh. 5.7 - Prob. 109ECh. 5.7 - Prob. 110ECh. 5.7 - Prob. 111ECh. 5.7 - Prob. 112ECh. 5.7 - Prob. 113ECh. 5.7 - Prob. 114ECh. 5.7 - Prob. 115ECh. 5.7 - Prob. 116ECh. 5.7 - Prob. 117ECh. 5.7 - Prob. 118ECh. 5.7 - Prob. 119ECh. 5.7 - Prob. 120ECh. 5.7 - Prob. 121ECh. 5.7 - Prob. 122ECh. 5.7 - Prob. 123ECh. 5.7 - Prob. 124ECh. 5.7 - Prob. 125ECh. 5.7 - The bar graph shows changes in the percentage of...Ch. 5.7 - Prob. 127ECh. 5.7 - Prob. 128ECh. 5.7 - Prob. 129ECh. 5.7 - Prob. 130ECh. 5.7 - Prob. 131ECh. 5.7 - Prob. 132ECh. 5.7 - The table shows the population of California for...Ch. 5.7 - In Exercises 133-134, you will develop geometric...Ch. 5.7 - Prob. 135ECh. 5.7 - Prob. 136ECh. 5.7 - Prob. 137ECh. 5.7 - Prob. 138ECh. 5.7 - Prob. 139ECh. 5.7 - Prob. 140ECh. 5.7 - Prob. 141ECh. 5.7 - Prob. 142ECh. 5.7 - Make Sense? In Exercises 142-145, determine...Ch. 5.7 - Prob. 144ECh. 5.7 - Prob. 145ECh. 5.7 - Prob. 146ECh. 5.7 - Prob. 147ECh. 5.7 - Prob. 148ECh. 5.7 - Prob. 149ECh. 5.7 - Prob. 150ECh. 5.7 - Prob. 151ECh. 5.7 - Prob. 152ECh. 5.7 - Prob. 153ECh. 5.7 - Prob. 154ECh. 5.7 - Prob. 155ECh. 5 - In Exercises 1 and 2, determine whether the number...Ch. 5 - In Exercises 1 and 2, determine whether the number...Ch. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - In Exercises 6-8, find the greatest common divisor...Ch. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Prob. 17RECh. 5 - Prob. 18RECh. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Perform the indicated operations in Exercises...Ch. 5 - Perform the indicated operations in Exercises...Ch. 5 - Perform the indicated operations in Exercises...Ch. 5 - Perform the indicated operations in Exercises...Ch. 5 - Perform the indicated operations in Exercises...Ch. 5 - Perform the indicated operations in Exercises...Ch. 5 - 29. For the year 2015, the Congressional Budget...Ch. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - In Exercises 41-44, express each terminating...Ch. 5 - In Exercises 41-44, express each terminating...Ch. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 46RECh. 5 - Prob. 47RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 51RECh. 5 - Prob. 52RECh. 5 - Prob. 53RECh. 5 - Prob. 54RECh. 5 - Prob. 55RECh. 5 - Prob. 56RECh. 5 - Prob. 57RECh. 5 - Prob. 58RECh. 5 - Prob. 59RECh. 5 - Prob. 60RECh. 5 - Prob. 61RECh. 5 - Prob. 62RECh. 5 - Prob. 63RECh. 5 - Prob. 64RECh. 5 - Prob. 65RECh. 5 - In Exercises 63-66, simplify the square root. 300Ch. 5 - Prob. 67RECh. 5 - Prob. 68RECh. 5 - Prob. 69RECh. 5 - Prob. 70RECh. 5 - Prob. 71RECh. 5 - Prob. 72RECh. 5 - Prob. 73RECh. 5 - Prob. 74RECh. 5 - Prob. 75RECh. 5 - Prob. 76RECh. 5 - Prob. 77RECh. 5 - Prob. 78RECh. 5 - Prob. 79RECh. 5 - Prob. 80RECh. 5 - Prob. 81RECh. 5 - Prob. 82RECh. 5 - Prob. 83RECh. 5 - Prob. 84RECh. 5 - Prob. 85RECh. 5 - Prob. 86RECh. 5 - Prob. 87RECh. 5 - Prob. 88RECh. 5 - Prob. 89RECh. 5 - Prob. 90RECh. 5 - Prob. 91RECh. 5 - Prob. 92RECh. 5 - 93. Shown in the figure is a 5-hour clock and the...Ch. 5 - In Exercises 94-104, evaluate each expression. 94....Ch. 5 - Prob. 95RECh. 5 - Prob. 96RECh. 5 - Prob. 97RECh. 5 - Prob. 98RECh. 5 - Prob. 99RECh. 5 - Prob. 100RECh. 5 - Prob. 101RECh. 5 - Prob. 102RECh. 5 - Prob. 103RECh. 5 - Prob. 104RECh. 5 - Prob. 105RECh. 5 - Prob. 106RECh. 5 - Prob. 107RECh. 5 - Prob. 108RECh. 5 - Prob. 109RECh. 5 - Prob. 110RECh. 5 - Prob. 111RECh. 5 - Prob. 112RECh. 5 - Prob. 113RECh. 5 - Prob. 114RECh. 5 - Prob. 115RECh. 5 - Prob. 116RECh. 5 - Prob. 117RECh. 5 - Prob. 118RECh. 5 - Prob. 119RECh. 5 - In Exercises 119-122, perform the indicated...Ch. 5 - Prob. 121RECh. 5 - Prob. 122RECh. 5 - Prob. 123RECh. 5 - Prob. 124RECh. 5 - Prob. 125RECh. 5 - Prob. 126RECh. 5 - Prob. 127RECh. 5 - Prob. 128RECh. 5 - Prob. 129RECh. 5 - Prob. 130RECh. 5 - Prob. 131RECh. 5 - Prob. 132RECh. 5 - Prob. 133RECh. 5 - Prob. 134RECh. 5 - In Exercises 135-137, write the first six terms of...Ch. 5 - Prob. 136RECh. 5 - Prob. 137RECh. 5 - Prob. 138RECh. 5 - Prob. 139RECh. 5 - Prob. 140RECh. 5 - Prob. 141RECh. 5 - Prob. 142RECh. 5 - Prob. 143RECh. 5 - Prob. 144RECh. 5 - Prob. 145RECh. 5 - Prob. 146RECh. 5 - Prob. 147RECh. 5 - Prob. 148RECh. 5 - 1. Which of the numbers 2, 3, 4, 5, 6, 8, 9, 10,...Ch. 5 - Prob. 2TCh. 5 - Prob. 3TCh. 5 - Prob. 4TCh. 5 - Prob. 5TCh. 5 - Prob. 6TCh. 5 - Prob. 7TCh. 5 - 8. Express as a quotient of integers in lowest...Ch. 5 - Prob. 9TCh. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - Prob. 12TCh. 5 - Prob. 13TCh. 5 - Prob. 14TCh. 5 - Prob. 15TCh. 5 - Prob. 16TCh. 5 - Prob. 17TCh. 5 - Prob. 18TCh. 5 - Prob. 19TCh. 5 - Prob. 20TCh. 5 - Prob. 21TCh. 5 - Prob. 22TCh. 5 - Prob. 23TCh. 5 - Prob. 24TCh. 5 - Prob. 25TCh. 5 - Prob. 26TCh. 5 - Prob. 27TCh. 5 - Prob. 28TCh. 5 - Prob. 29TCh. 5 - 30. Find , the seventh term of the geometric...
Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
Probability & Statistics (28 of 62) Basic Definitions and Symbols Summarized; Author: Michel van Biezen;https://www.youtube.com/watch?v=21V9WBJLAL8;License: Standard YouTube License, CC-BY
Introduction to Probability, Basic Overview - Sample Space, & Tree Diagrams; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=SkidyDQuupA;License: Standard YouTube License, CC-BY