Chapter 54, Problem 7A

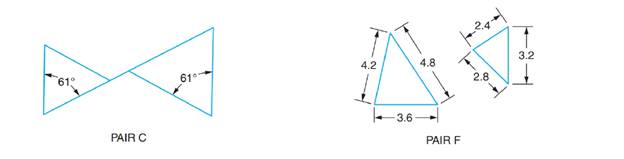
Determine which of the following pairs of triangles (A through F) are similar. All linear dimensions are in inches.
The similar pairs of triangles are

To determine

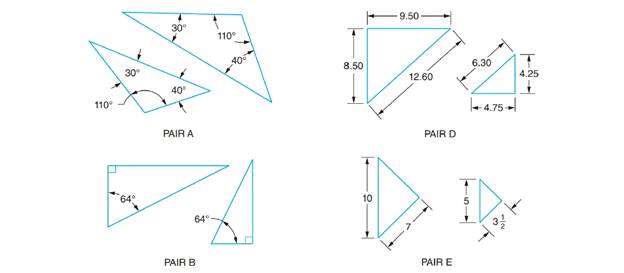
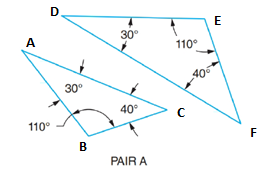
(a)

Similarity of triangle.

Answer to Problem 7A

Triangles are similar.

Explanation of Solution

Given information:

  

Calculation:

In ΔABC and ΔDEF

  $\begin{array}{l}\angle BAC=\angle EDF\\ \angle ABC=\angle DEF\\ \angle BCA=\angle EFD\end{array}$

  $\Delta ABCℿ<mi>D</mi><mi>E</mi><mi>F</mi>$

To determine

(b)

Similarity of triangle.

Answer to Problem 7A

Triangles are similar.

Explanation of Solution

Given information:

  

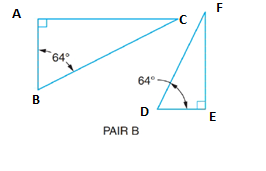
Calculation:

In ΔABC and ΔDEF

  $\begin{array}{l}\angle BAC=\angle DEF\\ \angle ABC=\angle EDF\end{array}$

  $\angle BCA=\angle EFD$ (Property of triangle)

Hence,

  $\Delta ABCℿ<mi>D</mi><mi>E</mi><mi>F</mi>$

To determine

(c)

Similarity of triangle.

Answer to Problem 7A

Triangles are similar.

Explanation of Solution

Given information:

  

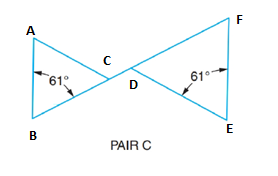
Calculation:

In ΔABC and ΔDEF

  $\angle ABC=\angle DEF$ (Given)

  $\angle ACB=\angle EDF$ (Vertically opposite angle)

  $\angle BAC=\angle DFE$ (By properties of triangle)

  $\Delta ABCℿ\Delta DEF$

To determine

(d)

Similarity of triangle.

Answer to Problem 7A

Triangles are similar.

Explanation of Solution

Given information:

  

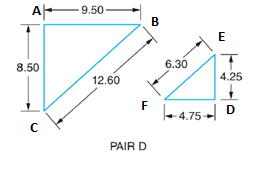
Calculation:

In ΔABC and ΔDEF

  $\begin{array}{l}\frac{AB}{FD}=\frac{9.50}{4.75}\\ \frac{AB}{FD}=2\end{array}$

  $\begin{array}{l}\frac{AC}{ED}=\frac{8.50}{4.25}\\ \frac{AC}{ED}=2\end{array}$

  $\begin{array}{l}\frac{BC}{EF}=\frac{12.60}{6.30}\\ \frac{BC}{EF}=2\end{array}$

  $\Delta ABCℿ<mi>D</mi><mi>E</mi><mi>F</mi>$ (Ratio of corresponding lines are equal)

To determine

(e)

Similarity of triangle.

Answer to Problem 7A

Triangles are not similar.

Explanation of Solution

Given information:

  

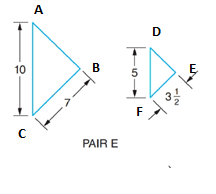
Calculation:

In ΔABC And ΔDEF

  $\begin{array}{l}\frac{AC}{DF}=\frac{10}{5}\\ \frac{AC}{DF}=2\end{array}$

  $\begin{array}{l}\frac{BC}{EF}=\frac{7}{3\frac{1}{2}}\\ \frac{BC}{EF}=2\end{array}$

But $\frac{AB}{DE}$ is not given.

Hence, ΔABC And ΔDEF are not similar.

To determine

(f)

Similarity of triangle.

Answer to Problem 7A

Triangles are similar.

Explanation of Solution

Given information:

  

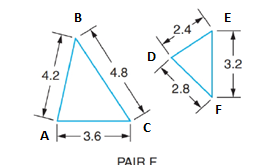
Calculation:

In ΔABC And ΔDEF

  $\begin{array}{l}\frac{AB}{DF}=\frac{4.2}{2.8}\\ \frac{AB}{DF}=\frac{3}{2}\\ \frac{BC}{EF}=\frac{4.8}{3.2}\\ \frac{BC}{EF}=\frac{3}{2}\\ \frac{AC}{DE}=\frac{3.6}{2.4}\\ \frac{AC}{DE}=\frac{3}{2}\\ \Delta ABCℿ\Delta DEF\end{array}$

Hence, ΔABC And ΔDEF are similar.