EBK WEBASSIGN FOR STEWART'S ESSENTIAL C
2nd Edition
ISBN: 9781337772198
Author: Stewart
Publisher: VST
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 5.4, Problem 1E
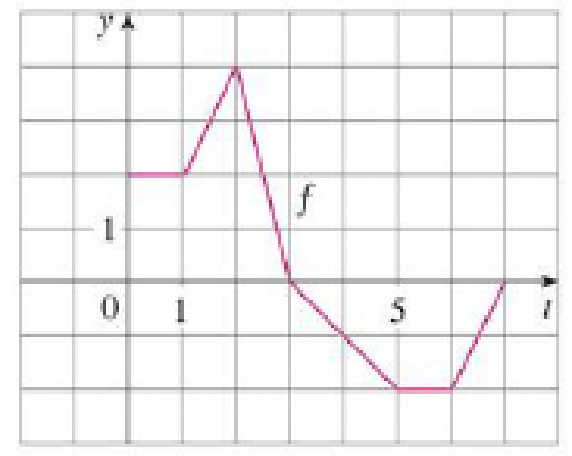
Let
(a) Evaluate g(0), g(1), g(2), g(3), and g(6).
(b) On what interval is g increasing?
(c) Where does g have a maximum value?
(d) Sketch a rough graph of g.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Consider the function f(x) = x²-1.
(a) Find the instantaneous rate of change of f(x) at x=1 using the definition of the derivative.
Show all your steps clearly.
(b) Sketch the graph of f(x) around x = 1. Draw the secant line passing through the points on the
graph where x 1 and x->
1+h (for a small positive value of h, illustrate conceptually). Then,
draw the tangent line to the graph at x=1. Explain how the slope of the tangent line relates to the
value you found in part (a).
(c) In a few sentences, explain what the instantaneous rate of change of f(x) at x = 1 represents in
the context of the graph of f(x). How does the rate of change of this function vary at different
points?
1. The graph of ƒ is given. Use the graph to evaluate each of the following values. If a value does not exist,
state that fact.
и
(a) f'(-5)
(b) f'(-3)
(c) f'(0)
(d) f'(5)
2. Find an equation of the tangent line to the graph of y = g(x) at x = 5 if g(5) = −3 and g'(5)
=
4.
-
3. If an equation of the tangent line to the graph of y = f(x) at the point where x 2 is y = 4x — 5, find ƒ(2)
and f'(2).
Does the series converge or diverge
Chapter 5 Solutions
EBK WEBASSIGN FOR STEWART'S ESSENTIAL C
Ch. 5.1 - Prob. 1ECh. 5.1 - (a) Use six rectangles to find estimates of each...Ch. 5.1 - (a) Estimate the area under the graph of f(x)=x...Ch. 5.1 - Prob. 3ECh. 5.1 - (a) Estimate the area under the graph of f(x) = 1...Ch. 5.1 - Prob. 6ECh. 5.1 - Prob. 7ECh. 5.1 - Prob. 8ECh. 5.1 - The speed of a runner increased steadily during...Ch. 5.1 - Speedometer readings for a motorcycle at 12-second...
Ch. 5.1 - Prob. 11ECh. 5.1 - Prob. 12ECh. 5.1 - The velocity graph of a braking car is shown. Use...Ch. 5.1 - Prob. 14ECh. 5.1 - Use Definition 2 to find an expression for the...Ch. 5.1 - Prob. 16ECh. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - (a) Let An be the area of a polygon with n equal...Ch. 5.2 - Evaluate the Riemann sum for f(x)=312x,2x14, with...Ch. 5.2 - Prob. 2ECh. 5.2 - If f(x)=ex2, 0 x 2, find the Riemann sum with n...Ch. 5.2 - Prob. 4ECh. 5.2 - Prob. 5ECh. 5.2 - Find the Riemann sum for f (x) = x + x2, 2x0, if...Ch. 5.2 - Prob. 7ECh. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Prob. 13ECh. 5.2 - Prob. 14ECh. 5.2 - Express the limit as a definite integral on the...Ch. 5.2 - Prob. 16ECh. 5.2 - Prob. 17ECh. 5.2 - Prob. 18ECh. 5.2 - Prob. 19ECh. 5.2 - Use the form of the definition of the integral...Ch. 5.2 - Prob. 21ECh. 5.2 - Prob. 22ECh. 5.2 - Prob. 23ECh. 5.2 - Prob. 24ECh. 5.2 - Prob. 25ECh. 5.2 - 25–26 Express the integral as a limit of Riemann...Ch. 5.2 - Prob. 29ECh. 5.2 - Prob. 30ECh. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - Evaluate the integral by interpreting it in terms...Ch. 5.2 - 31–36 Evaluate the integral by interpreting it in...Ch. 5.2 - 3136 Evaluate the integral by interpreting it in...Ch. 5.2 - Evaluate sin2xcos4xdx.Ch. 5.2 - Given that 013xx2+4dx=558, what is 103uu2+4du?Ch. 5.2 - Write as a single integral in the form abf(x)dx:...Ch. 5.2 - If 15f(x)dx=12 and 45f(x)dx=3.6, find 14f(x)dx.Ch. 5.2 - If 09f(x)dx=37 and 09g(x)dx=16, find...Ch. 5.2 - Find 05f(x)dx if f(x)={3forx3xforx3Ch. 5.2 - In Example 2 in Section 5.1 we showed that...Ch. 5.2 - If , F(x)=2xf(t)dt, where f is the function whose...Ch. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - 61. Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Use Property 8 to estimate the value of the...Ch. 5.2 - Express the limit as a definite integral....Ch. 5.3 - 32. Evaluate the integral.
Ch. 5.3 - Evaluate the integral. 01coshtdtCh. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 35ECh. 5.3 - Prob. 36ECh. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 69ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 70ECh. 5.3 - Prob. 45ECh. 5.3 - Find the general indefinite integral. (x3+x23)dxCh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Prob. 43ECh. 5.3 - Prob. 48ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 1ECh. 5.3 - Prob. 2ECh. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Prob. 8ECh. 5.3 - Prob. 9ECh. 5.3 - Prob. 10ECh. 5.3 - Prob. 11ECh. 5.3 - Evaluate the integral. 14yyy2dyCh. 5.3 - Prob. 13ECh. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Prob. 17ECh. 5.3 - Prob. 18ECh. 5.3 - Prob. 20ECh. 5.3 - Prob. 21ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - Prob. 28ECh. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 49ECh. 5.3 - Prob. 50ECh. 5.3 - Prob. 51ECh. 5.3 - Prob. 52ECh. 5.3 - Prob. 53ECh. 5.3 - Prob. 54ECh. 5.3 - Prob. 55ECh. 5.3 - Prob. 56ECh. 5.3 - Prob. 57ECh. 5.3 - Prob. 58ECh. 5.3 - Prob. 59ECh. 5.3 - 5960 The velocity function (in meters per second)...Ch. 5.3 - Prob. 61ECh. 5.3 - Prob. 62ECh. 5.3 - Prob. 65ECh. 5.3 - Prob. 63ECh. 5.3 - Prob. 64ECh. 5.3 - Prob. 66ECh. 5.3 - Prob. 67ECh. 5.3 - Prob. 68ECh. 5.4 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.4 - Let g(x)=0xf(t)dt, where f is the function whose...Ch. 5.4 - Sketch the area represented by g(x). Then find...Ch. 5.4 - Prob. 4ECh. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - Use Part 1 of the Fundamental Theorem of Calculus...Ch. 5.4 - Find the derivative of the function....Ch. 5.4 - 514 Use Part 1 of the Fundamental Theorem of...Ch. 5.4 - On what interval is the curve y=0xt2t2+t+2dt...Ch. 5.4 - Prob. 24ECh. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 25ECh. 5.4 - Prob. 26ECh. 5.4 - Find a function f and a number a such that...Ch. 5.4 - A manufacturing company owns a major piece of...Ch. 5.4 - A high-tech company purchases a new computing...Ch. 5.4 - Find the average value of the function on the...Ch. 5.4 - 15-18 Find the average value of the function on...Ch. 5.4 - Find the average value of the function on the...Ch. 5.4 - Find the average value of the function on the...Ch. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Prob. 21ECh. 5.4 - Prob. 22ECh. 5.5 - Evaluate the integral by making the given...Ch. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Evaluate the indefinite integral. x2ex3dxCh. 5.5 - Prob. 9ECh. 5.5 - Prob. 10ECh. 5.5 - Evaluate the indefinite integral. (lnx)2xdxCh. 5.5 - Prob. 12ECh. 5.5 - Prob. 13ECh. 5.5 - Prob. 14ECh. 5.5 - Prob. 20ECh. 5.5 - Prob. 16ECh. 5.5 - Prob. 17ECh. 5.5 - Prob. 18ECh. 5.5 - Prob. 15ECh. 5.5 - Prob. 25ECh. 5.5 - Evaluate the indefinite integral. sinh2xcoshxdxCh. 5.5 - Evaluate the indefinite integral. sin(lnx)xdxCh. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5.5 - Prob. 19ECh. 5.5 - Prob. 26ECh. 5.5 - Prob. 27ECh. 5.5 - Prob. 28ECh. 5.5 - Prob. 29ECh. 5.5 - Prob. 30ECh. 5.5 - Prob. 31ECh. 5.5 - Prob. 32ECh. 5.5 - Prob. 36ECh. 5.5 - Evaluate the indefinite integral. 1+x1+x2dxCh. 5.5 - Prob. 33ECh. 5.5 - Prob. 34ECh. 5.5 - Prob. 37ECh. 5.5 - Prob. 38ECh. 5.5 - Evaluate the definite integral. 011+7x3dxCh. 5.5 - Evaluate the definite integral. 03dx5x+1Ch. 5.5 - Prob. 41ECh. 5.5 - Prob. 42ECh. 5.5 - Prob. 43ECh. 5.5 - Prob. 44ECh. 5.5 - Prob. 50ECh. 5.5 - Prob. 45ECh. 5.5 - Prob. 48ECh. 5.5 - Evaluate the definite integral. ee4dxxlnxCh. 5.5 - Prob. 49ECh. 5.5 - Prob. 47ECh. 5.5 - Evaluate the indefinite integral. /2/2x2sinx1+x6dxCh. 5.5 - Prob. 52ECh. 5.5 - Prob. 57ECh. 5.5 - 78. Evaluate by making a substitution and...Ch. 5.5 - Prob. 59ECh. 5.5 - Prob. 60ECh. 5.5 - Prob. 61ECh. 5.5 - Prob. 62ECh. 5.5 - Prob. 63ECh. 5.5 - Prob. 64ECh. 5.5 - Prob. 65ECh. 5.5 - Prob. 66ECh. 5.5 - 89. If f is continuous on , prove that
For the...Ch. 5.5 - Prob. 68ECh. 5.5 - Prob. 69ECh. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 54ECh. 5.5 - Prob. 56ECh. 5.5 - Find the average value of the function on the...Ch. 5 - Prob. 1RCCCh. 5 - Prob. 2RCCCh. 5 - Prob. 3RCCCh. 5 - Prob. 6RCCCh. 5 - Prob. 4RCCCh. 5 - Prob. 7RCCCh. 5 - Prob. 5RCCCh. 5 - Prob. 9RCCCh. 5 - Prob. 10RCCCh. 5 - Prob. 1RQCh. 5 - Prob. 2RQCh. 5 - Prob. 3RQCh. 5 - Prob. 4RQCh. 5 - Prob. 5RQCh. 5 - Prob. 6RQCh. 5 - Prob. 7RQCh. 5 - Prob. 8RQCh. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 10RQCh. 5 - Prob. 11RQCh. 5 - Prob. 12RQCh. 5 - Prob. 13RQCh. 5 - 14. Determine whether the statement is true or...Ch. 5 - Prob. 15RQCh. 5 - Prob. 16RQCh. 5 - Determine whether the statement is true or false....Ch. 5 - Prob. 18RQCh. 5 - Prob. 1RECh. 5 - Prob. 2RECh. 5 - Prob. 3RECh. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Evaluate the integral, if it exists. 01(1x9)dxCh. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Prob. 12RECh. 5 - Prob. 13RECh. 5 - Prob. 14RECh. 5 - Prob. 16RECh. 5 - Prob. 15RECh. 5 - Prob. 18RECh. 5 - Evaluate the integral, if it exists....Ch. 5 - Prob. 20RECh. 5 - Prob. 19RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Evaluate the integral, if it exists. cos(lnx)xdxCh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Prob. 35RECh. 5 - Prob. 36RECh. 5 - Prob. 37RECh. 5 - Prob. 38RECh. 5 - Prob. 39RECh. 5 - Prob. 40RECh. 5 - Prob. 41RECh. 5 - A particle moves along a line with velocity...Ch. 5 - Prob. 43RECh. 5 - Prob. 44RECh. 5 - Prob. 45RECh. 5 - Prob. 48RECh. 5 - Prob. 49RECh. 5 - Prob. 50RECh. 5 - Prob. 8RCCCh. 5 - Prob. 46RECh. 5 - If f is a continuous function, what is the limit...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Suppose that a particle moves along a straight line with velocity v (t) = 62t, where 0 < t <3 (v(t) in meters per second, t in seconds). Find the displacement d (t) at time t and the displacement up to t = 3. d(t) ds = ["v (s) da = { The displacement up to t = 3 is d(3)- meters.arrow_forwardLet f (x) = x², a 3, and b = = 4. Answer exactly. a. Find the average value fave of f between a and b. fave b. Find a point c where f (c) = fave. Enter only one of the possible values for c. c=arrow_forwardplease do Q3arrow_forward
- Use the properties of logarithms, given that In(2) = 0.6931 and In(3) = 1.0986, to approximate the logarithm. Use a calculator to confirm your approximations. (Round your answers to four decimal places.) (a) In(0.75) (b) In(24) (c) In(18) 1 (d) In ≈ 2 72arrow_forwardFind the indefinite integral. (Remember the constant of integration.) √tan(8x) tan(8x) sec²(8x) dxarrow_forwardFind the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forward
- a -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forwardEvaluate F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line π 1 1 segment starting at the point (8, ' and ending at the point (3, 2 3'6arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY