
CALCULUS,VOLUME 1 (OER)
17th Edition
ISBN: 2810022307715
Author: OpenStax
Publisher: XANEDU C
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 5.2, Problem 70E
In the following exercises, evaluate the
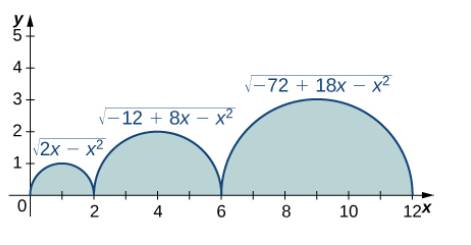
70.
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
No chatgpt pls
Remix
4. Direction Fields/Phase Portraits. Use the given direction fields to plot solution curves
to each of the given initial value problems.
(a)
x = x+2y
1111
y = -3x+y
with x(0) = 1, y(0) = -1
(b) Consider the initial value problem corresponding to the given phase portrait.
x = y
y' = 3x + 2y
Draw two "straight line solutions"
passing through (0,0)
(c) Make guesses for the equations of the straight line solutions: y = ax.
It was homework
Chapter 5 Solutions
CALCULUS,VOLUME 1 (OER)
Ch. 5.1 - State whether the given sums are equal or unequal....Ch. 5.1 - In the following exercises, use the rules for sums...Ch. 5.1 - In the following exercises, use the rules for sums...Ch. 5.1 - Suppose that i=1100ai=15 and i=1100bi=12 . In the...Ch. 5.1 - Suppose that i=1100ai=15 and i=1100bi=12 . In the...Ch. 5.1 - Suppose that i=1100ai=15 and i=1100bi=12 . In the...Ch. 5.1 - Suppose that i=1100ai=15 and i=1100bi=12 . In the...Ch. 5.1 - In the following exercises, use summation...Ch. 5.1 - In the following exercises, use summation...Ch. 5.1 - In the following exercises, use summation...
Ch. 5.1 - In the following exercises, use summation...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Let Ln denote the left-endpoint sum using n sub...Ch. 5.1 - Compute the left and tight Riemann sums— L4 and R4...Ch. 5.1 - Compute the left and light Riemann sums— L6 and R6...Ch. 5.1 - Compute the left and light Riemann sums— L4 and R4...Ch. 5.1 - Compute the left and right Riemann sums— L6 and R6...Ch. 5.1 - Express the following endpoint sums in sigma...Ch. 5.1 - Express the following endpoint sums in sigma...Ch. 5.1 - Express the following endpoint sums in sigma...Ch. 5.1 - Express the following endpoint sums in sigma...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - In the following exercises, graph the function...Ch. 5.1 - To help get in shape, Joe gets a new pair of...Ch. 5.1 - The following table gives approximate values of...Ch. 5.1 - The following table gives the approximate increase...Ch. 5.1 - The following table gives the approximate increase...Ch. 5.1 - The following table gives the percent growth of...Ch. 5.1 - In the following exercises, estimate the areas...Ch. 5.1 - In the following exercises, estimate the areas...Ch. 5.1 - In the following exercises, estimate the areas...Ch. 5.1 - In the following exercises, estimate the areas...Ch. 5.1 - [T] Use a computer algebra system to compute the...Ch. 5.1 - [T] Use a computer algebra system to compute the...Ch. 5.1 - [T] Use a computer algebra system to compute the...Ch. 5.1 - In the following exercises, use a calculator or a...Ch. 5.1 - In the following exercises, use a calculator or a...Ch. 5.1 - In the following exercises, use a calculator or a...Ch. 5.1 - In the following exercises, use a calculator or a...Ch. 5.1 - In the following exercises, use a calculator or a...Ch. 5.1 - Explain why, if f(b)0 and f is decreasing on [a,...Ch. 5.1 - Show that, in general, RNLN=(ba)f(b)f(a)N .Ch. 5.1 - Explain why, if f is increasing on |a,b| , the...Ch. 5.1 - For each of the three graphs: Obtain a lower bound...Ch. 5.1 - In the previous exercise, explain why L(A) gets no...Ch. 5.1 - A unit circle is made up of n wedges equivalent to...Ch. 5.2 - In the following exercises, express the limits as...Ch. 5.2 - In the following exercises, express the limits as...Ch. 5.2 - In the following exercises, express the limits as...Ch. 5.2 - In the following exercises, express the limits as...Ch. 5.2 - In the following exercises, given Ln or Rn as...Ch. 5.2 - In the following exercises, given Ln or Rn as...Ch. 5.2 - In the following exercises, given Ln or Rn as...Ch. 5.2 - In the following exercises, given Ln or Rn as...Ch. 5.2 - In the following exercises, given Ln or Rn as...Ch. 5.2 - In the following exercises, given Ln or Rn as...Ch. 5.2 - In the following exercises, evaluate the integrals...Ch. 5.2 - In the following exercises, evaluate the integrals...Ch. 5.2 - In the following exercises, evaluate the integrals...Ch. 5.2 - In the following exercises, evaluate the integrals...Ch. 5.2 - In the following exercises, evaluate the integrals...Ch. 5.2 - In the following exercises, evaluate the integrals...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, evaluate the integral...Ch. 5.2 - In the following exercises, use averages of values...Ch. 5.2 - In the following exercises, use averages of values...Ch. 5.2 - In the following exercises, use averages of values...Ch. 5.2 - In the following exercises, use averages of values...Ch. 5.2 - Suppose that 04f(x)dx=5 and 02f(x)dx=3 , and...Ch. 5.2 - Suppose that 04f(x)dx=5 and 02f(x)dx=3 , and...Ch. 5.2 - Suppose that 04f(x)dx=5 and 02f(x)dx=3 , and...Ch. 5.2 - Suppose that 04f(x)dx=5 and 02f(x)dx=3 , and...Ch. 5.2 - Suppose that 04f(x)dx=5 and 02f(x)dx=3 , and...Ch. 5.2 - Suppose that 04f(x)dx=5 and 02f(x)dx=3 , and...Ch. 5.2 - In the following exercises, use the identity...Ch. 5.2 - In the following exercises, use the identity...Ch. 5.2 - In the following exercises, use the identity...Ch. 5.2 - In the following exercises, use the identity...Ch. 5.2 - In the following exercises, given that...Ch. 5.2 - In the following exercises, given that...Ch. 5.2 - In the following exercises, given that...Ch. 5.2 - In the following exercises, given that...Ch. 5.2 - In the following exercises, given that...Ch. 5.2 - In the following exercises, given that...Ch. 5.2 - In the following exercises, use the comparison...Ch. 5.2 - In the following exercises, use the comparison...Ch. 5.2 - In the following exercises, use the comparison...Ch. 5.2 - In the following exercises, use the comparison...Ch. 5.2 - In the following exercises, use the comparison...Ch. 5.2 - In the following exercises, use the comparison...Ch. 5.2 - In the following exercises, find the average value...Ch. 5.2 - In the following exercises, find the average value...Ch. 5.2 - In the following exercises, find the average value...Ch. 5.2 - In the following exercises, find the average value...Ch. 5.2 - In the following exercises, find the average value...Ch. 5.2 - In the following exercises, find the average value...Ch. 5.2 - In the following exercises, approximate the...Ch. 5.2 - In the following exercises, approximate the...Ch. 5.2 - the following exercises, approximate the average...Ch. 5.2 - In the following exercises, approximate the...Ch. 5.2 - In the following exercises, compute the average...Ch. 5.2 - In the following exercises, compute the average...Ch. 5.2 - In the following exercises, compute the average...Ch. 5.2 - [T] y=xsin(x2) over the interval [,0] ; the exact...Ch. 5.2 - Suppose that A=02sin2tdt and B=02cos2tdt . Show...Ch. 5.2 - Suppose that A=/4/4sec2tdt= and B=/4/4tan2tdt= ....Ch. 5.2 - Show that the average value of sin2t over [0,2] is...Ch. 5.2 - Show that the average value of cos2t over [0,2] is...Ch. 5.2 - Explain why the graphs of a quadratic function...Ch. 5.2 - Suppose that parabola p(x)=ax2+bx+c opens downward...Ch. 5.2 - Suppose [a, b] can be subdivided into subintervals...Ch. 5.2 - Suppose f and g are continuous functions such that...Ch. 5.2 - Suppose the average value of f over [a, b] is 1...Ch. 5.2 - Suppose that [a, b] can be partitioned, taking...Ch. 5.2 - Suppose that for each i such that 1iN one has...Ch. 5.2 - Suppose that for each i such that 1iN one has...Ch. 5.2 - [T] Compute the left and right Riemann sums L10...Ch. 5.2 - [T] Compute the left and right Riemann sums, L10...Ch. 5.2 - If 151+t4dt=41.7133..., what is 151+u4du ?Ch. 5.2 - Estimate 01tdt using the left and right endpoint...Ch. 5.2 - Estimate 01tdt by comparison with the area of a...Ch. 5.2 - From the graph of sin(2x) shown: a. Explain why...Ch. 5.2 - If f is 1-periodic (f(t+1)=f(t)) , odd, and...Ch. 5.2 - If f is 1-periodic and 01f(t)dt=A , is it...Ch. 5.3 - How long after she exits the aircraft does Julie...Ch. 5.3 - Based on your answer to question 1, set up an...Ch. 5.3 - If Julie pulls her ripcord at an altitude of 3000...Ch. 5.3 - Julie pulls her ripcord at 3000 ft. It takes 5 sec...Ch. 5.3 - How long does it take Julie to reach terminal...Ch. 5.3 - Before pulling her ripcord, Julie reorients her...Ch. 5.3 - Answer the following question based on the...Ch. 5.3 - Consider two athletes running at variable speeds...Ch. 5.3 - Two mountain climbers start their climb at base...Ch. 5.3 - To get on a certain toll road a driver has to take...Ch. 5.3 - Set F(x)=1x(1t)dt . Find F(2) and the average...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - In the following exercises, use the Fundamental...Ch. 5.3 - The graph of y=0xf(t)dt , where f is a piecewise...Ch. 5.3 - The graph of y=0xf(t)dt , where f is a piecewise...Ch. 5.3 - The graph of y=0xl(t)dt , where l is a piecewise...Ch. 5.3 - The graph of y=0xl(t)dt , where l is a piecewise...Ch. 5.3 - In the following exercises, use a calculator to...Ch. 5.3 - In the following exercises, use a calculator to...Ch. 5.3 - In the following exercises, use a calculator to...Ch. 5.3 - In the following exercises, use a calculator to...Ch. 5.3 - In the following exercises, use a calculator to...Ch. 5.3 - In the following exercises, use a calculator to...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, evaluate each definite...Ch. 5.3 - In the following exercises, use the evaluation...Ch. 5.3 - In the following exercises, use the evaluation...Ch. 5.3 - In the following exercises, use the evaluation...Ch. 5.3 - In the following exercises, use the evaluation...Ch. 5.3 - In the following exercises, identify the roots of...Ch. 5.3 - In the following exercises, identify the roots of...Ch. 5.3 - In the following exercises, identify the roots of...Ch. 5.3 - In the following exercises, identify the roots of...Ch. 5.3 - Suppose that the number of hours of daylight on a...Ch. 5.3 - Suppose the rate of gasoline consumption in the...Ch. 5.3 - Explain why, if f is continuous over [a, b], there...Ch. 5.3 - Explain why, if f is continuous over [a, b] and is...Ch. 5.3 - Kepler’s first law states that the planets move in...Ch. 5.3 - A point on an ellipse with major axis length 2a...Ch. 5.3 - As implied earlier, according to Kepler's laws,...Ch. 5.3 - The force of gravitational attraction between the...Ch. 5.3 - The displacement from rest of a mass attached to a...Ch. 5.4 - Use basic integration formulas to compute the...Ch. 5.4 - Use basic integration formulas to compute the...Ch. 5.4 - Use basic integration formulas to compute the...Ch. 5.4 - Use basic integration formulas to compute the...Ch. 5.4 - Use basic integration formulas to compute the...Ch. 5.4 - Use basic integration formulas to compute the...Ch. 5.4 - Write an integral that expresses the increase in...Ch. 5.4 - Write an integral that quantifies the change in...Ch. 5.4 - A regular N-gon (an N-sided polygon with sides...Ch. 5.4 - The area of a regular pentagon with side length a0...Ch. 5.4 - A dodecahedron is a Platonic solid with a surface...Ch. 5.4 - An icosahedron is a Platonic solid with a surface...Ch. 5.4 - Write an integral that quantifies the change in...Ch. 5.4 - Write an integral that quantifies the increase in...Ch. 5.4 - Write an integral that quantifies the increase in...Ch. 5.4 - Write an integral that quantifies the increase in...Ch. 5.4 - Suppose that a particle moves along a straight...Ch. 5.4 - Suppose that a particle moves along a straight...Ch. 5.4 - Suppose that a particle moves along a straight...Ch. 5.4 - Suppose that a particle moves along a straight...Ch. 5.4 - A ball is thrown upward from a height of 1.5 m at...Ch. 5.4 - A ball is thrown upward from a height of 3 m at an...Ch. 5.4 - The area A(t) of a circular shape is growing at a...Ch. 5.4 - A spherical balloon is being inflated at a...Ch. 5.4 - Water flows into a conical tank with...Ch. 5.4 - A horizontal cylindrical tank has cross-sectional...Ch. 5.4 - The following table lists the electrical power in...Ch. 5.4 - The average residential electrical power use (in...Ch. 5.4 - The data in the following table are use to...Ch. 5.4 - The data in the following table are used to...Ch. 5.4 - The distribution of incomes as of 2012 in the...Ch. 5.4 - Newton’s law of gravity states that the...Ch. 5.4 - For a given motor vehicle, the maximum achievable...Ch. 5.4 - John is a 25-year old man who weighs 160 lb. He...Ch. 5.4 - Sandra is a 25-year old woman who weighs 120 lb....Ch. 5.4 - A motor vehicle has a maximum efficiency of 33 mpg...Ch. 5.4 - Although some engines are more efficient at given...Ch. 5.4 - [T] The following table lists the 2013 schedule of...Ch. 5.4 - [T] The following table provides hypothetical data...Ch. 5.4 - [T] The graph below plots the quadratic...Ch. 5.4 - [T] the graph below plots the cubic...Ch. 5.4 - [T] Suppose you go on a road trip and record your...Ch. 5.4 - [T] The accompanying graph plots the best...Ch. 5.4 - [T] Using your acceleration equation from the...Ch. 5.4 - [T] Using your velocity equation from the previous...Ch. 5.4 - [T] The number of hamburgers sold at a restaurant...Ch. 5.4 - [T] An athlete runs by a motion detector, which...Ch. 5.5 - Why is u-substitution referred to as change of...Ch. 5.5 - 2. If f=gh, when reversing the chain title,...Ch. 5.5 - In the following exercises, verify each identity...Ch. 5.5 - In the following exercises, verify each identity...Ch. 5.5 - In the following exercises, verify each identity...Ch. 5.5 - In the following exercises, verify each identity...Ch. 5.5 - In the following exercises, verify each identity...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, find the...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a suitable change...Ch. 5.5 - In the following exercises, use a calculator to...Ch. 5.5 - In the following exercises, use a calculator to...Ch. 5.5 - In the following exercises, use a calculator to...Ch. 5.5 - In the following exercises, use a calculator to...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, evaluate the...Ch. 5.5 - In the following exercises, evaluate the...Ch. 5.5 - In the following exercises, evaluate the...Ch. 5.5 - In the following exercises, evaluate the...Ch. 5.5 - In the following exercises, evaluate the...Ch. 5.5 - In the following exercises, evaluate the...Ch. 5.5 - If h(a)=h(b) in abg(h(x))h(xdx) , what can you say...Ch. 5.5 - Is the substitution u=1x2 in the definite integral...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - In the following exercises, use a change of...Ch. 5.5 - Show that the average value of f(x) over an...Ch. 5.5 - Find the area under the graph of f(t)=t(1+ t 2)a...Ch. 5.5 - Find the area under the graph of g(t)=t(1 t 2)a...Ch. 5.5 - The area of a semicircle of radius 1 can be...Ch. 5.5 - The area of the top half of an ellipse with a...Ch. 5.5 - [T] The following graph is of a function of the...Ch. 5.5 - [T] The following graph is of a function of the...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, compute each...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, find each indefinite...Ch. 5.6 - In the following exercises, verify by...Ch. 5.6 - In the following exercises, verify by...Ch. 5.6 - In the following exercises, verify by...Ch. 5.6 - In the following exercises, verify by...Ch. 5.6 - Write an integral to express the area under the...Ch. 5.6 - Write an integral to express the area under the...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, use appropriate...Ch. 5.6 - In the following exercises, evaluate the definite...Ch. 5.6 - In the following exercises, evaluate the definite...Ch. 5.6 - In the following exercises, evaluate the definite...Ch. 5.6 - In the following exercises, evaluate the definite...Ch. 5.6 - In the following exercises, evaluate the definite...Ch. 5.6 - In the following exercises, integrate using the...Ch. 5.6 - In the following exercises, integrate using the...Ch. 5.6 - In the following exercises, integrate using the...Ch. 5.6 - In the following exercises, integrate using the...Ch. 5.6 - In the following exercises, integrate using the...Ch. 5.6 - In the following exercises, integrate using the...Ch. 5.6 - In the following exercises, does the right-end...Ch. 5.6 - In the following exercises, does the right-end...Ch. 5.6 - In the following exercises, does the right-end...Ch. 5.6 - In the following exercises, does the right-end...Ch. 5.6 - In the following exercises, does the right-end...Ch. 5.6 - In the following exercises, does the right-end...Ch. 5.6 - In the following exercises, f(x)0 for axb. Find...Ch. 5.6 - In the following exercises, f(x)0 for axb. Find...Ch. 5.6 - In the following exercises, f(x)0 for axb. Find...Ch. 5.6 - In the following exercises, f(x)0 for axb. Find...Ch. 5.6 - Find the area under the graph of the function...Ch. 5.6 - Compute the integral of f(x)=xex2 and find the...Ch. 5.6 - Find the limit, as N tends to infinity, of the...Ch. 5.6 - Show that abdtt= 1/b 1/a dt t when 0ab .Ch. 5.6 - Suppose that f(x)0 for all x and that f and g are...Ch. 5.6 - Use the previous exercise to find the derivative...Ch. 5.6 - Show that if c0 , then the integral of 1/x from ac...Ch. 5.6 - The following exercises are intended to derive the...Ch. 5.6 - The following exercises are intended to derive the...Ch. 5.6 - Use the identity Inx=1xdtx show that In(x) is an...Ch. 5.6 - Pretend, for the moment, that we do not know that...Ch. 5.6 - Pretend, for the moment, that we do not know that...Ch. 5.6 - The sine integral, defined as S(x)=0xsinttdt is an...Ch. 5.6 - [T] The normal distribution in probability is...Ch. 5.6 - [T] Compute the right endpoint estimates R50 and...Ch. 5.7 - In the following exercises, evaluate each integral...Ch. 5.7 - In the following exercises, evaluate each integral...Ch. 5.7 - In the following exercises, evaluate each integral...Ch. 5.7 - In the following exercises, evaluate each integral...Ch. 5.7 - In the following exercises, evaluate each integral...Ch. 5.7 - In the following exercises, evaluate each integral...Ch. 5.7 - In the following exercises, find each indefinite...Ch. 5.7 - In the following exercises, find each indefinite...Ch. 5.7 - In the following exercises, find each indefinite...Ch. 5.7 - In the following exercises, find each indefinite...Ch. 5.7 - In the following exercises, find each indefinite...Ch. 5.7 - In the following exercises, find each indefinite...Ch. 5.7 - Explain the relationship cos1t+C=dt 1t2 =sin1t+C ....Ch. 5.7 - Explain the relationship sec1t+C=dt|t| t2...Ch. 5.7 - Explain what is wrong with the following integral:...Ch. 5.7 - Explain what is wrong with the following integral:...Ch. 5.7 - In the following exercises, solve for the...Ch. 5.7 - In the following exercises, solve for the...Ch. 5.7 - In the following exercises, solve for the...Ch. 5.7 - In the following exercises, solve for the...Ch. 5.7 - In the following exercises, compute the...Ch. 5.7 - In the following exercises, compute the...Ch. 5.7 - In the following exercises, compute the...Ch. 5.7 - In the following exercises, compute the...Ch. 5.7 - In the following exercises, compute the...Ch. 5.7 - In the following exercises, compute the...Ch. 5.7 - In the following exercises, use a calculator to...Ch. 5.7 - In the following exercises, use a calculator to...Ch. 5.7 - In the following exercises, use a calculator to...Ch. 5.7 - In the following exercises, use a calculator to...Ch. 5.7 - In the following exercises, use a calculator to...Ch. 5.7 - In the following exercises, use a calculator to...Ch. 5.7 - In the following exercises, compute each integral...Ch. 5.7 - In the following exercises, compute each integral...Ch. 5.7 - In the following exercises, compute each integral...Ch. 5.7 - In the following exercises, compute each integral...Ch. 5.7 - In the following exercises, compute each integral...Ch. 5.7 - In the following exercises, compute each integral...Ch. 5.7 - In the following exercises, compute each definite...Ch. 5.7 - In the following exercises, compute each definite...Ch. 5.7 - In the following exercises, compute each definite...Ch. 5.7 - In the following exercises, compute each definite...Ch. 5.7 - For A0 , compute I(A)=AAdt1+t2 and evaluate...Ch. 5.7 - For 1B , compute I(B)=1Bdtt t2 1 and evaluate...Ch. 5.7 - Use the substitution u=2cotx and the identity...Ch. 5.7 - [T] Approximate the points at which the graphs of...Ch. 5.7 - . [T] Approximate the points at which the graphs...Ch. 5.7 - Use the following graph to prove that...Ch. 5 - True or False. Justify your answer with a proof or...Ch. 5 - True or False. Justify your answer with a proof or...Ch. 5 - True or False. Justify your answer with a proof or...Ch. 5 - All continuous functions have antiderivative....Ch. 5 - y=3x22x+1 over [1,1]Ch. 5 - y=In(x2+1) over [0,e]Ch. 5 - y=x2sinx over [0,]Ch. 5 - y=x+1x over [1,4]Ch. 5 - Evaluate the following integrals. 447....Ch. 5 - Evaluate the following integrals. 448. 043t 1+6t2...Ch. 5 - Evaluate the following integrals. 449....Ch. 5 - Evaluate the following integrals. 450. 0/4ecos 2...Ch. 5 - Find the antiderivative. 451. dx ( x+4 )3Ch. 5 - Find the antiderivative. 452. xIn(x2)dxCh. 5 - Find the antiderivative. 453. 4x2 1x6 dxCh. 5 - Find the antiderivative. 454. e 2x1+e 4xdxCh. 5 - Find the derivative. 455. ddt0tsinx 1+x2 dxCh. 5 - Find the derivative 456. ddx1x34t2dtCh. 5 - Find the derivative. 457. ddx1In(x)(4t+et)dtCh. 5 - Find the derivative. 458. ddx0cosxet2dtCh. 5 - The following problems consider the historic...Ch. 5 - The following problems consider the historic...Ch. 5 - The following problems consider the historic...Ch. 5 - The velocity of a bullet from a rifle can be...Ch. 5 - What is the average velocity of the bullet for the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
CHECK POINT 1 Write a word description of the set L = {a, b, c, d, e, f}.
Thinking Mathematically (6th Edition)
29-36. Total and Annual Returns. Compute the total and annual returns on the following investments.
29. Five ye...
Using and Understanding Mathematics: A Quantitative Reasoning Approach (6th Edition)
Find the counterclockwise circulation and outward flux of the field around and over the boundary of the region...
University Calculus: Early Transcendentals (4th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Sketch the graph of y= x . (p. 22)
Precalculus
Answer each of the following and explain your answer. a. How many lines can contain a particular segment? b. Ho...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- No chatgpt pls will upvotearrow_forward(7) (12 points) Let F(x, y, z) = (y, x+z cos yz, y cos yz). Ꮖ (a) (4 points) Show that V x F = 0. (b) (4 points) Find a potential f for the vector field F. (c) (4 points) Let S be a surface in R3 for which the Stokes' Theorem is valid. Use Stokes' Theorem to calculate the line integral Jos F.ds; as denotes the boundary of S. Explain your answer.arrow_forward(3) (16 points) Consider z = uv, u = x+y, v=x-y. (a) (4 points) Express z in the form z = fog where g: R² R² and f: R² → R. (b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate steps otherwise no credit. (c) (4 points) Let S be the surface parametrized by T(x, y) = (x, y, ƒ (g(x, y)) (x, y) = R². Give a parametric description of the tangent plane to S at the point p = T(x, y). (d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic approximation) of F = (fog) at a point (a, b). Verify that Q(x,y) F(a+x,b+y). =arrow_forward
- (6) (8 points) Change the order of integration and evaluate (z +4ry)drdy . So S√ ² 0arrow_forward(10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward
- (9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward(8) (12 points) (a) (8 points) Let C be the circle x² + y² = 4. Let F(x, y) = (2y + e²)i + (x + sin(y²))j. Evaluate the line integral JF. F.ds. Hint: First calculate V x F. (b) (4 points) Let S be the surface r² + y² + z² = 4, z ≤0. Calculate the flux integral √(V × F) F).dS. Justify your answer.arrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. a = 13, b = 15, C = 68° Law of Sines Law of Cosines Then solve the triangle. (Round your answers to four decimal places.) C = 15.7449 A = 49.9288 B = 62.0712 × Need Help? Read It Watch Itarrow_forward
- (4) (10 points) Evaluate √(x² + y² + z²)¹⁄² exp[}(x² + y² + z²)²] dV where D is the region defined by 1< x² + y²+ z² ≤4 and √√3(x² + y²) ≤ z. Note: exp(x² + y²+ 2²)²] means el (x²+ y²+=²)²]¸arrow_forward(2) (12 points) Let f(x,y) = x²e¯. (a) (4 points) Calculate Vf. (b) (4 points) Given x directional derivative 0, find the line of vectors u = D₁f(x, y) = 0. (u1, 2) such that the - (c) (4 points) Let u= (1+3√3). Show that Duƒ(1, 0) = ¦|▼ƒ(1,0)| . What is the angle between Vf(1,0) and the vector u? Explain.arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a b 29 39 66.50 C 17.40 d 0 54.0 126° a Ꮎ b darrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Definite Integral Calculus Examples, Integration - Basic Introduction, Practice Problems; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=rCWOdfQ3cwQ;License: Standard YouTube License, CC-BY