
MATHEMATICAL EXCURSIONS>LL<
4th Edition
ISBN: 9780357097977
Author: Aufmann
Publisher: CENGAGE LEARNING (CUSTOM)
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 5.1, Problem 16ES
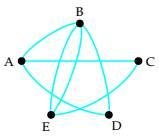
(a) determine whether the graph is Eulerian. If it is, find an Euler circuit. If it is not, explain why. (b)If the graph does not have an Euler circuit, does it have an Euler path? If so, find one. If not, explain why.
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
Remix
4. Direction Fields/Phase Portraits. Use the given direction fields to plot solution curves
to each of the given initial value problems.
(a)
x = x+2y
1111
y = -3x+y
with x(0) = 1, y(0) = -1
(b) Consider the initial value problem corresponding to the given phase portrait.
x = y
y' = 3x + 2y
Draw two "straight line solutions"
passing through (0,0)
(c) Make guesses for the equations of the straight line solutions: y = ax.
It was homework
No chatgpt pls will upvote
Chapter 5 Solutions
MATHEMATICAL EXCURSIONS>LL<
Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - A pen-tracing puzzle is given. See if you can find...Ch. 5.1 - Explain why the following pen-tracing puzzle is...Ch. 5.1 - Transportation An X in the table below indicates a...Ch. 5.1 - Transportation The table below shows the nonstop...Ch. 5.1 - Social Network A group of friends is represented...Ch. 5.1 - Prob. 4ESCh. 5.1 - Determine (a) the number of edges in the graph,...
Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine (a) the number of edges in the graph,...Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Determine whether the two graphs are equivalent.Ch. 5.1 - Explain why the following two graphs cannot be...Ch. 5.1 - Label the vertices of the second graph so that it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - (a) determine whether the graph is Eulerian. If it...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Parks in Exercises 23 and 24, a map of a park is...Ch. 5.1 - Transportation For the train routes given in...Ch. 5.1 - Transportation For the direct air flights given in...Ch. 5.1 - Pets The diagram below shows the arrangement of a...Ch. 5.1 - Transportation A subway map is shown below. Is it...Ch. 5.1 - Prob. 29ESCh. 5.1 - Prob. 30ESCh. 5.1 - Degrees of Separation In the graph below, an edge...Ch. 5.1 - Social Network In the graph below, an edge...Ch. 5.1 - Prob. 33ESCh. 5.1 - Travel A map of South America is shown at the...Ch. 5.2 - Continue investigating Hamiltonian circuits in...Ch. 5.2 - Use the greedy algorithm and the weighted graph...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Use Dirac's theorem to verify that the graph is...Ch. 5.2 - Transportation For the train routes given in...Ch. 5.2 - Transportation For the direct air flights given in...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use trial and error to find two Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the greedy algorithm to find a Hamiltonian...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Use the edge-picking algorithm to find a...Ch. 5.2 - Travel A company representative lives in...Ch. 5.2 - Travel A tourist is staying in Toronto, Canada,...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Use the edge-picking algorithm to design a...Ch. 5.2 - Travel Nicole wants to tour Asia. She will start...Ch. 5.2 - Travel The prices for traveling between five...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Travel Use the edge-picking algorithm to find a...Ch. 5.2 - Route Planning Brian needs to visit the pet store,...Ch. 5.2 - Route Planning A bike messenger needs to deliver...Ch. 5.2 - Scheduling A research company has a large...Ch. 5.2 - Computer Networks A small office wishes to network...Ch. 5.2 - Route Planning A security officer patrolling a...Ch. 5.2 - Route Planning A city engineer needs to inspect...Ch. 5.2 - Draw a connected graph with six vertices that has...Ch. 5.2 - Assign weights to the edges of the following...Ch. 5.3 - The tetrahedron in figure 5.20 consists of four...Ch. 5.3 - The following graph is the projection of one ofthe...Ch. 5.3 - Prob. 3EECh. 5.3 - Give a reason why the graph below Cannot be the...Ch. 5.3 - Prob. 1ESCh. 5.3 - Prob. 2ESCh. 5.3 - Prob. 3ESCh. 5.3 - Prob. 4ESCh. 5.3 - Prob. 5ESCh. 5.3 - Prob. 6ESCh. 5.3 - Prob. 7ESCh. 5.3 - Prob. 8ESCh. 5.3 - Prob. 9ESCh. 5.3 - Prob. 10ESCh. 5.3 - Prob. 11ESCh. 5.3 - Prob. 12ESCh. 5.3 - Show that the following graph contracts to K5.Ch. 5.3 - Show that the following graph contracts to the...Ch. 5.3 - Prob. 15ESCh. 5.3 - Prob. 16ESCh. 5.3 - Prob. 17ESCh. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Count the number of vertices, edges, and faces,...Ch. 5.3 - Prob. 23ESCh. 5.3 - Prob. 24ESCh. 5.3 - Prob. 25ESCh. 5.3 - Prob. 26ESCh. 5.3 - Prob. 27ESCh. 5.3 - Prob. 28ESCh. 5.3 - Prob. 29ESCh. 5.3 - Prob. 30ESCh. 5.4 - A one-way road ends at a two-way street. The...Ch. 5.4 - A one-way road intersects a two-way road in a...Ch. 5.4 - A two-way road intersects another two-way road in...Ch. 5.4 - Prob. 1ESCh. 5.4 - Prob. 2ESCh. 5.4 - Prob. 3ESCh. 5.4 - Prob. 4ESCh. 5.4 - Prob. 5ESCh. 5.4 - Prob. 6ESCh. 5.4 - Prob. 7ESCh. 5.4 - Prob. 8ESCh. 5.4 - Prob. 9ESCh. 5.4 - Prob. 10ESCh. 5.4 - Prob. 11ESCh. 5.4 - Prob. 12ESCh. 5.4 - Prob. 13ESCh. 5.4 - Prob. 14ESCh. 5.4 - Prob. 15ESCh. 5.4 - Prob. 16ESCh. 5.4 - Prob. 17ESCh. 5.4 - Prob. 18ESCh. 5.4 - Prob. 19ESCh. 5.4 - Prob. 20ESCh. 5.4 - Prob. 21ESCh. 5.4 - Prob. 22ESCh. 5.4 - Scheduling Six different groups of children would...Ch. 5.4 - Scheduling Five different charity organizations...Ch. 5.4 - Scheduling Students in a film class have...Ch. 5.4 - Animal Housing A researcher has discovered six new...Ch. 5.4 - Prob. 27ESCh. 5.4 - Prob. 28ESCh. 5.4 - Prob. 29ESCh. 5.4 - Prob. 30ESCh. 5.4 - Scheduling Edge colorings, as explained in...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - (a) determine the number of edges in the graph,...Ch. 5 - Soccer In the table below, an X indicates teams...Ch. 5 - Each vertex in the graph at the left represents a...Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Determine whether the two graphs are equivalent.Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Find an Euler path if possible, and (b) find an...Ch. 5 - Prob. 10RECh. 5 - Prob. 11RECh. 5 - Architecture The floor plan of a sculpture gallery...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Use Dirac's theorem to verify that the graph is...Ch. 5 - Prob. 15RECh. 5 - Prob. 16RECh. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Use the edge-picking algorithm to find a...Ch. 5 - Efficient Route The distances, in miles, between...Ch. 5 - Computer Networking A small office needs to...Ch. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - Prob. 25RECh. 5 - Prob. 26RECh. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Count the number of vertices, edges, and faces in...Ch. 5 - Prob. 29RECh. 5 - Prob. 30RECh. 5 - Prob. 31RECh. 5 - Prob. 32RECh. 5 - Prob. 33RECh. 5 - Prob. 34RECh. 5 - Scheduling A company has scheduled a retreat at a...Ch. 5 - Social Network Each vertex in the graph at the...Ch. 5 - Determine whether the following two graphs are...Ch. 5 - Answer the following questions for the graph shown...Ch. 5 - Recreation The illustration below depicts bridges...Ch. 5 - a. What does Dirac's theorem state? Explain how it...Ch. 5 - Low-Cost Route The table below shows the cost of...Ch. 5 - Use the greedy algorithm to find a Hamiltonian...Ch. 5 - Prob. 8TCh. 5 - Answer the following questions for the graph shown...Ch. 5 - Prob. 10TCh. 5 - Prob. 11TCh. 5 - A group of eight friends is planning a vacation in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- (7) (12 points) Let F(x, y, z) = (y, x+z cos yz, y cos yz). Ꮖ (a) (4 points) Show that V x F = 0. (b) (4 points) Find a potential f for the vector field F. (c) (4 points) Let S be a surface in R3 for which the Stokes' Theorem is valid. Use Stokes' Theorem to calculate the line integral Jos F.ds; as denotes the boundary of S. Explain your answer.arrow_forward(3) (16 points) Consider z = uv, u = x+y, v=x-y. (a) (4 points) Express z in the form z = fog where g: R² R² and f: R² → R. (b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate steps otherwise no credit. (c) (4 points) Let S be the surface parametrized by T(x, y) = (x, y, ƒ (g(x, y)) (x, y) = R². Give a parametric description of the tangent plane to S at the point p = T(x, y). (d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic approximation) of F = (fog) at a point (a, b). Verify that Q(x,y) F(a+x,b+y). =arrow_forward(6) (8 points) Change the order of integration and evaluate (z +4ry)drdy . So S√ ² 0arrow_forward
- (10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward
- (8) (12 points) (a) (8 points) Let C be the circle x² + y² = 4. Let F(x, y) = (2y + e²)i + (x + sin(y²))j. Evaluate the line integral JF. F.ds. Hint: First calculate V x F. (b) (4 points) Let S be the surface r² + y² + z² = 4, z ≤0. Calculate the flux integral √(V × F) F).dS. Justify your answer.arrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. a = 13, b = 15, C = 68° Law of Sines Law of Cosines Then solve the triangle. (Round your answers to four decimal places.) C = 15.7449 A = 49.9288 B = 62.0712 × Need Help? Read It Watch Itarrow_forward(4) (10 points) Evaluate √(x² + y² + z²)¹⁄² exp[}(x² + y² + z²)²] dV where D is the region defined by 1< x² + y²+ z² ≤4 and √√3(x² + y²) ≤ z. Note: exp(x² + y²+ 2²)²] means el (x²+ y²+=²)²]¸arrow_forward
- (2) (12 points) Let f(x,y) = x²e¯. (a) (4 points) Calculate Vf. (b) (4 points) Given x directional derivative 0, find the line of vectors u = D₁f(x, y) = 0. (u1, 2) such that the - (c) (4 points) Let u= (1+3√3). Show that Duƒ(1, 0) = ¦|▼ƒ(1,0)| . What is the angle between Vf(1,0) and the vector u? Explain.arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a b 29 39 66.50 C 17.40 d 0 54.0 126° a Ꮎ b darrow_forwardAnswer the following questions related to the following matrix A = 3 ³).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY