Chapter 5.1, Problem 16E

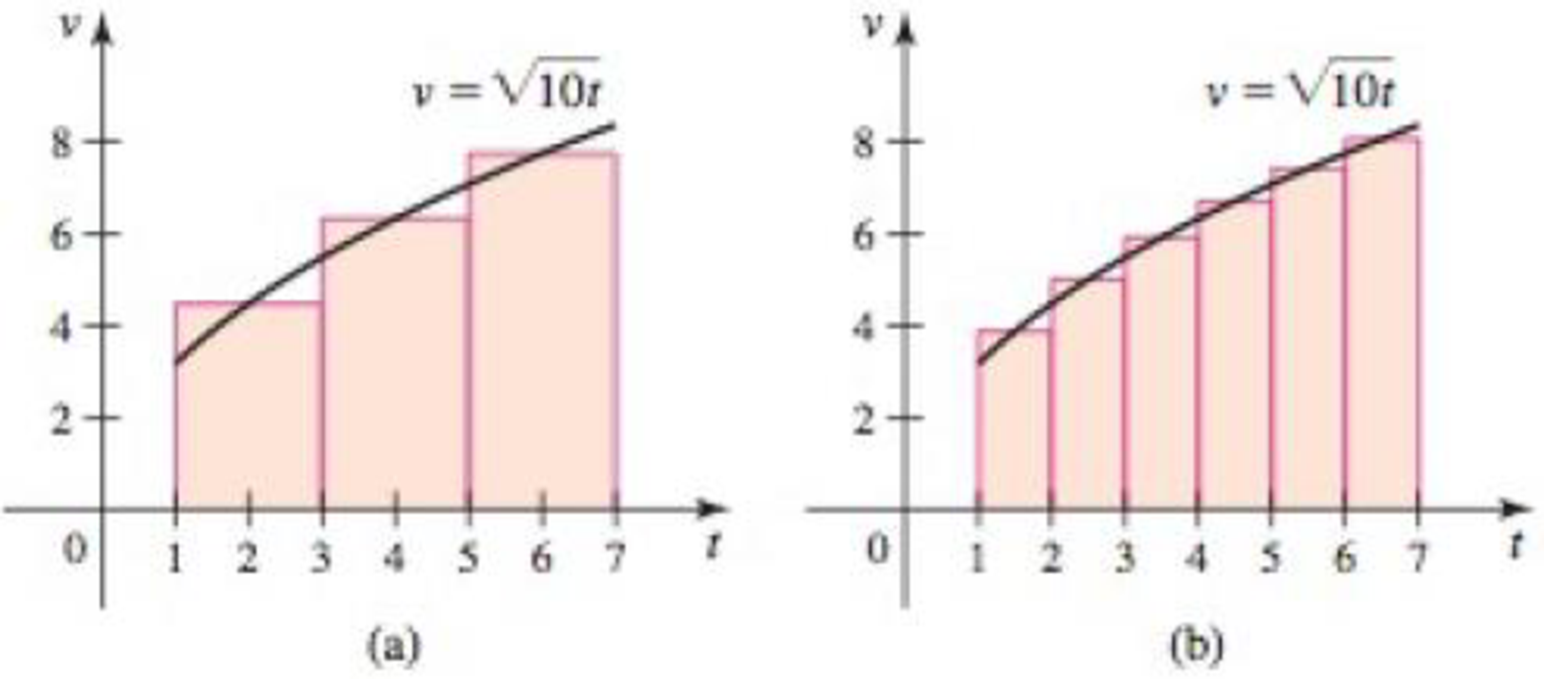
Approximating displacement The velocity in ft/s of an object moving along a line is given by $v=\sqrt{10t}$ on the interval 1 ≤ t ≤ 7.

1. a. Divide the time interval [1, 7] into n = 3 subintervals. [1, 3], [3, 5], and [5, 7]. On each subinterval, assume the object moves at a constant velocity equal to v evaluated at the midpoint of the subinterval and use these approximations to estimate the displacement of the object on [1, 7] (see part (a) of the figure).
2. b. Repeat part (a) for n = 6 subintervals (see part (b) of the figure).