Student Solutions Manual, Chapters 1-11 for Stewart's Single Variable Calculus, 8th (James Stewart Calculus)
8th Edition
ISBN: 9781305271814
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 5, Problem 5P
(a) Show that the volume of a segment of height h of a sphere of radius r is
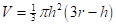
(See the figure.)
(b) Show that if a sphere of radius 1 is sliced by a plane at a distance x from the center in such a way that the volume of one segment is twice the volume of the other, then x is a solution of the equation
3x3 – 9x + 2 = 0
where 0 < x < 1. Use Newton’s method to find x accurate to four decimal places.
(c) Using the formula for the volume of a segment of a sphere, it can he shown that the depth x to which a floating sphere of radius r sinks in water is a root of the equation
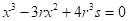
where s is the specific gravity of the sphere. Suppose a wooden sphere of radius 0.5 m has specific gravity 0.75. Calculate, to four-decimal-place accuracy, the depth to which the sphere will sink.
(d) A hemispherical bowl has radius 5 inches and water is running into the bowl at the rate of 0.2 in3/s.
(i) How fast is the water level in the bowl rising at the instant the water is 3 inches deep?
(ii) At a certain instant, the water is 4 inches deep. How long will it take to fill the bowl?
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Points z1 and z2 are shown on the graph.z1 is at (4 real,6 imaginary), z2 is at (-5 real, 2 imaginary)Part A: Identify the points in standard form and find the distance between them.Part B: Give the complex conjugate of z2 and explain how to find it geometrically.Part C: Find z2 − z1 geometrically and explain your steps.
A polar curve is represented by the equation r1 = 7 + 4cos θ.Part A: What type of limaçon is this curve? Justify your answer using the constants in the equation.Part B: Is the curve symmetrical to the polar axis or the line θ = pi/2 Justify your answer algebraically.Part C: What are the two main differences between the graphs of r1 = 7 + 4cos θ and r2 = 4 + 4cos θ?
A curve, described by x2 + y2 + 8x = 0, has a point A at (−4, 4) on the curve.Part A: What are the polar coordinates of A? Give an exact answer.Part B: What is the polar form of the equation? What type of polar curve is this?Part C: What is the directed distance when Ø = 5pi/6 Give an exact answer.
Chapter 5 Solutions
Student Solutions Manual, Chapters 1-11 for Stewart's Single Variable Calculus, 8th (James Stewart Calculus)
Ch. 5.1 - Find the area of the shaded region.Ch. 5.1 - Find the area of the shaded region.Ch. 5.1 - Find the area of the shaded region.Ch. 5.1 - Find the area of the shaded region.Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Prob. 6ECh. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Prob. 8ECh. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Sketch the region enclosed by the given curves....
Ch. 5.1 - Prob. 11ECh. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Prob. 13ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 17ECh. 5.1 - Prob. 18ECh. 5.1 - Prob. 19ECh. 5.1 - Prob. 20ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 22ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 25ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 27ECh. 5.1 - Prob. 28ECh. 5.1 - Prob. 29ECh. 5.1 - Prob. 30ECh. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Evaluate the integral and interpret it as the area...Ch. 5.1 - Prob. 37ECh. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Graph the region between the curves and use your...Ch. 5.1 - Prob. 43ECh. 5.1 - Prob. 44ECh. 5.1 - Use a computer algebra system to find the exact...Ch. 5.1 - Prob. 46ECh. 5.1 - Racing cars driven by Chris and Kelly are side by...Ch. 5.1 - The widths (in meters) of a kidney-shaped swimming...Ch. 5.1 - A cross-section of an airplane wing is shown....Ch. 5.1 - If the birth rate of a population is b(t) = 2200 +...Ch. 5.1 - In Example 5, we modeled a measles pathogenesis...Ch. 5.1 - The rates at which rain fell, in inches per hour,...Ch. 5.1 - Two cars, A and B, start side by side and...Ch. 5.1 - The figure shows graphs of the marginal revenue...Ch. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Prob. 57ECh. 5.1 - (a) Find the number a such that the line x = a...Ch. 5.1 - Find the values of c such that the area of the...Ch. 5.1 - Prob. 60ECh. 5.1 - Prob. 61ECh. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - For what values of m do the line y = mx and the...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Prob. 11ECh. 5.2 - Prob. 12ECh. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 15ECh. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 18ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 22ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 24ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 28ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 30ECh. 5.2 - Set up an integral for the volume of the solid...Ch. 5.2 - Set up an integral for the volume of the solid...Ch. 5.2 - Set up an integral for the volume of the solid...Ch. 5.2 - Prob. 34ECh. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Use a computer algebra system to find the exact...Ch. 5.2 - Use a computer algebra system to find the exact...Ch. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - A CAT scan produces equally spaced cross-sectional...Ch. 5.2 - Prob. 44ECh. 5.2 - Prob. 45ECh. 5.2 - Prob. 46ECh. 5.2 - Prob. 47ECh. 5.2 - Find the volume of the described solid S. 48.A...Ch. 5.2 - Find the volume of the described solid S. 49.A cap...Ch. 5.2 - Find the volume of the described solid S. 50. A...Ch. 5.2 - Prob. 51ECh. 5.2 - Find the volume of the described solid S. 52. A...Ch. 5.2 - Prob. 53ECh. 5.2 - Find the volume of the described solid S. 54. The...Ch. 5.2 - Find the volume of the described solid S. 55. The...Ch. 5.2 - Prob. 56ECh. 5.2 - Prob. 57ECh. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Prob. 60ECh. 5.2 - Prob. 61ECh. 5.2 - The base of S is a circular disk with radius r....Ch. 5.2 - (a) Set up an integral for the volume of a solid...Ch. 5.2 - Prob. 64ECh. 5.2 - (a) Cavalieris Principle states that if a family...Ch. 5.2 - Find the volume common to two circular cylinders,...Ch. 5.2 - Prob. 67ECh. 5.2 - A bowl is shaped like a hemisphere with diameter...Ch. 5.2 - A hole of radius r is bored through the middle of...Ch. 5.2 - A hole of radius r is bored through the center of...Ch. 5.2 - Prob. 71ECh. 5.2 - Suppose that a region R has area A and lies above...Ch. 5.3 - Let S be the solid obtained by rotating the region...Ch. 5.3 - Let S be the solid obtained by rotating the region...Ch. 5.3 - Prob. 3ECh. 5.3 - Prob. 4ECh. 5.3 - Prob. 5ECh. 5.3 - Prob. 6ECh. 5.3 - Prob. 7ECh. 5.3 - Let V be the volume of the solid obtained by...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - (a) Set up an integral for the volume of the solid...Ch. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - Prob. 25ECh. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - If the region shown in the figure is rotated about...Ch. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Prob. 35ECh. 5.3 - Use a computer algebra system to find the exact...Ch. 5.3 - Prob. 37ECh. 5.3 - Prob. 38ECh. 5.3 - Prob. 39ECh. 5.3 - Prob. 40ECh. 5.3 - Prob. 41ECh. 5.3 - Prob. 42ECh. 5.3 - Prob. 43ECh. 5.3 - Let T be the triangular region with vertices (0,...Ch. 5.3 - Prob. 45ECh. 5.3 - Use cylindrical shells to find the volume of the...Ch. 5.3 - Prob. 47ECh. 5.3 - Suppose you make napkin rings by drilling holes...Ch. 5.4 - A 360-lb gorilla climbs a tree to a height of 20...Ch. 5.4 - How much work is done when a hoist lifts a 200-kg...Ch. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Shown is the graph of a force function (in...Ch. 5.4 - Prob. 6ECh. 5.4 - Prob. 7ECh. 5.4 - A spring has a natural length of 40 cm. If a 60-N...Ch. 5.4 - Suppose that 2 J of work is needed to stretch a...Ch. 5.4 - Prob. 10ECh. 5.4 - Prob. 11ECh. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Prob. 14ECh. 5.4 - Prob. 15ECh. 5.4 - Prob. 16ECh. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Prob. 18ECh. 5.4 - Prob. 19ECh. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Prob. 21ECh. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - When gas expands in a cylinder with radius r, the...Ch. 5.4 - In a steam engine the pressure P and volume V of...Ch. 5.4 - The kinetic energy KE of an object of mass m...Ch. 5.4 - Suppose that when launching an 800-kg roller...Ch. 5.4 - Prob. 33ECh. 5.4 - The Great Pyramid of King Khufu was built of...Ch. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 2ECh. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 4ECh. 5.5 - Prob. 5ECh. 5.5 - Prob. 6ECh. 5.5 - Prob. 7ECh. 5.5 - Prob. 8ECh. 5.5 - (a) Find the average value of f on the given...Ch. 5.5 - Prob. 10ECh. 5.5 - Prob. 11ECh. 5.5 - Prob. 12ECh. 5.5 - If f is continuous and 13f(x)dx=8, show that f...Ch. 5.5 - Prob. 14ECh. 5.5 - Find the average value of f on [0, 8].Ch. 5.5 - The velocity graph of an accelerating car is...Ch. 5.5 - Prob. 17ECh. 5.5 - The velocity v of blood that flows in a blood...Ch. 5.5 - The linear density in a rod 8 m long is...Ch. 5.5 - Prob. 20ECh. 5.5 - Prob. 21ECh. 5.5 - Use the diagram to show that if f is concave...Ch. 5.5 - Prob. 23ECh. 5.5 - Prob. 24ECh. 5 - (a) Draw two typical curves y = f(x) and y = g(x),...Ch. 5 - Prob. 2RCCCh. 5 - Prob. 3RCCCh. 5 - Prob. 4RCCCh. 5 - Prob. 5RCCCh. 5 - Prob. 6RCCCh. 5 - Prob. 1RECh. 5 - Find the area of the region bounded by the given...Ch. 5 - Find the area of the region bounded by the given...Ch. 5 - Prob. 4RECh. 5 - Prob. 5RECh. 5 - Prob. 6RECh. 5 - Prob. 7RECh. 5 - Prob. 8RECh. 5 - Prob. 9RECh. 5 - Prob. 10RECh. 5 - Find the volume of the solid obtained by rotating...Ch. 5 - Set up, but do not evaluate, an integral for the...Ch. 5 - Prob. 13RECh. 5 - Set up, but do not evaluate, an integral for the...Ch. 5 - Find the volumes of the solids obtained by...Ch. 5 - Let R be the region in the first quadrant bounded...Ch. 5 - Prob. 17RECh. 5 - Let R be the region bounded by the curves y = 1 ...Ch. 5 - Prob. 19RECh. 5 - Prob. 20RECh. 5 - Prob. 21RECh. 5 - Prob. 22RECh. 5 - Prob. 23RECh. 5 - Prob. 24RECh. 5 - The height of a monument is 20 m. A horizontal...Ch. 5 - Prob. 26RECh. 5 - Prob. 27RECh. 5 - Prob. 28RECh. 5 - A tank full of water has the shape of a paraboloid...Ch. 5 - A steel tank has the shape of a circular cylinder...Ch. 5 - Prob. 31RECh. 5 - (a) Find the average value of the function...Ch. 5 - If f is a continuous function, what is the limit...Ch. 5 - Let R1 be the region bounded by y = x2, y = 0, and...Ch. 5 - Prob. 1PCh. 5 - There is a line through the origin that divides...Ch. 5 - The figure shows a horizontal line y = c...Ch. 5 - A cylindrical glass of radius r and height L is...Ch. 5 - (a) Show that the volume of a segment of height h...Ch. 5 - Prob. 6PCh. 5 - Prob. 7PCh. 5 - Prob. 8PCh. 5 - The figure shows a curve C with the property that,...Ch. 5 - A paper drinking cup filled with water has the...Ch. 5 - A clepsydra, or water clock, is a glass container...Ch. 5 - A cylindrical container of radius r and height L...Ch. 5 - Prob. 13PCh. 5 - If the tangent at a point P on the curve y = x3...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- New folder 10. Find the area enclosed by the loop of the curve (1- t², t-t³)arrow_forward1. Graph and find the corresponding Cartesian equation for: t X== y = t +1 2 te(-∞, ∞) 42,369 I APR 27 F5 3 MacBook Air stv A Aa T 4 DIIarrow_forwardMiddle School GP... Echo home (1) Addition and su... Google Docs Netflix Netflix New folder 9. Find the area enclosed by x = sin²t, y = cost and the y-axis.arrow_forward
- 2. Graph and find the corresponding Cartesian equation for: (4 cos 0,9 sin 0) θ ε [0, 2π) 42,369 I APR 27 3 MacBook Air 2 tv A Aaarrow_forward30 Page< 3. Find the equation of the tangent line for x = 1+12, y = 1-3 at t = 2 42,369 APR A 27 M . tv NA 1 TAGN 2 Aa 7 MacBook Air #8arrow_forwardEvaluate the following integrals as they are writtenarrow_forward
- Calculus lll May I please have the blank lines completed, and final statement defined as a result? Thank you for the support!arrow_forward3. Consider the polynomial equation 6-iz+7z² - iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forwardForce with 800 N and 400 N are acting on a machine part at 30° and 60°, respectively with the positive x axisarrow_forward
- Find the accumulated amount A, if the principal P is invested at an interest rate of r per year for t years. (Round your answer to the nearest cent.) P = $13,000, r = 6%, t = 10, compounded quarterly A = $ 31902 Need Help? Read It Watch It Viewing Saved Work Revert to Last Response SUBMIT ANSWER O/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.003. EVIOUS ANSWERS ASK YOUR TEACHER PRACTICE ANOTHER Find the accumulated amount A, if the principal P is invested at an interest rate of r per year for t years. (Round your answer to the nearest cent.) P = $140,000, r = 8%, t = 8, compounded monthly A = $259130.20 X Need Help? Read It Watch Itarrow_forwardFind the present value of $20,000 due in 3 years at the given rate of interest. (Round your answers to the nearest cent.) (a) 2%/year compounded monthly (b) 5%/year compounded daily $ Need Help? Read It Watch It SUBMIT ANSWER [-/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.009. ASK YOUR TEACHER PRACTICE ANC Find the accumulated amount after 3 years if $4000 is invested at 3%/year compounded continuously. (Round your answer to the nearest cent.) Need Help? Read It Watch Itarrow_forwardFind the effective rate corresponding to the given nominal rate. (Round your answers to three decimal places.) (a) 9.5%/year compounded monthly % (b) 9.5%/year compounded daily % Need Help? Read It Watch It SUBMIT ANSWER -/6.66 Points] DETAILS MY NOTES TANAPCALC10 5.3.007. ASK YOUR TEACHE Find the present value of $90,000 due in 7 years at the given rate of interest. (Round your answers to the nearest cent.) (a) 9%/year compounded semiannually (b) 9%/year compounded quarterly LAarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
2.1 Introduction to inequalities; Author: Oli Notes;https://www.youtube.com/watch?v=D6erN5YTlXE;License: Standard YouTube License, CC-BY
GCSE Maths - What are Inequalities? (Inequalities Part 1) #56; Author: Cognito;https://www.youtube.com/watch?v=e_tY6X5PwWw;License: Standard YouTube License, CC-BY
Introduction to Inequalities | Inequality Symbols | Testing Solutions for Inequalities; Author: Scam Squad Math;https://www.youtube.com/watch?v=paZSN7sV1R8;License: Standard YouTube License, CC-BY