
The tension in each segment of the cable and the vertical distance between points
Answer to Problem 5.1P
The tension in segment
The tension in segment
The tension in segment
The vertical distance between points
Explanation of Solution
Concept Used:
Write the expression for the net moment about end
Here
Calculations:
The free body diagram for the system is shown below.
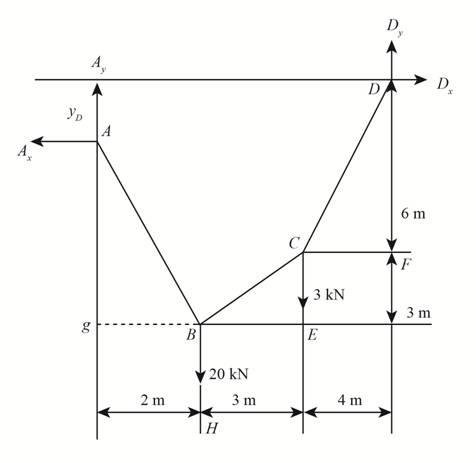
Figure-(1)
Here, the unknown vertical reactions are
The slope of cable
Write the moment about
Consider
Given
Given that
Therefore
Consider
Apply Pythagoras theorem in
Here, the distance between points
Substitute
Take square root on both sides.
Calculate
Substitute
Calculate
Substitute
Calculate
Substitute
The free body diagram at point C is shown below.
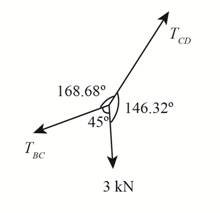
Figure-(2)
Apply Sine Law at point
Here, the tension in cable
Determine
Thus the tension in segment
Thus the tension in segment
Analyze point
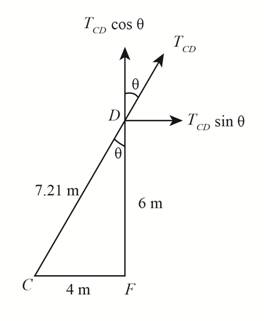
Figure-(3)
Apply Angle Sum Property in
Substitute
Calculate
Substitute
Calculate
Substitute
Calculate
Substitute
Consider
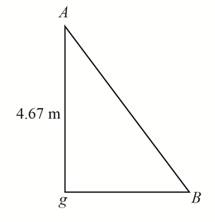
Figure-(4)
Calculate the length
Substitute
Calculate
Substitute
Analyze point
The free body diagram for point
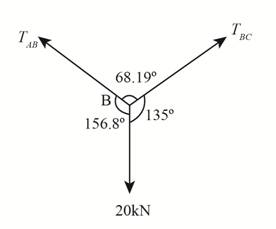
Figure-(5)
Substitute
Calculate
Substitute
Calculate
Substitute
Apply Sine Law at point
Here, the tension in cable
Determine
Thus the tension in segment
Conclusion:
The tension in segment
The tension in segment
The tension in segment
The vertical distance between points
Want to see more full solutions like this?
Chapter 5 Solutions
STRUCTURAL ANAL.W/MOD MASTERING ACCE
- 1. (20 Points) Determine the critical depth in the trapezoidal drainage ditch shown below. The slope of the ditch is 0.0016, the side slopes are 1V:2.5H, the bottom width is b = 14', and the design discharge is 500 cfs. At this discharge the depth is y = 4.25'. Also, determine the flow regime and calculate the Froude number. Ye= ? Z barrow_forward3. (20 Points) A broad crested weir, 10 feet high, will be constructed in a rectangular channel B feet wide. The weir crest extends a length of B = 120 feet between the banks with 2 - 4 foot wide, round nosed piers in the channel. The width of the weir crest is 8 feet. If H = 6', determine the design discharge for the weir.arrow_forwardParking Needs vs. Alternative Transportation Methods for presentation slides include images and graphsarrow_forward
- Please explain step by step and show formulararrow_forwardBeam ABD is supported and loaded as shown. The cross-section of the beam is also shown. The modulus of elasticity of the beam is 200 GPa. 6.0 kN/m Cross-section: 330 mm 4.5 kN 8.0 kNm 40 mm 2.5 m 1.5 m 20 mm Set up the discontinuity moment function in terms of x. List all the appropriate boundary conditions. Determine the slope function in terms of x. Determine the deflection function in terms of x. Determine the support reactions. Determine the maximum deflection. 290 mmarrow_forwardDraw the Shear Force Diagram and Bending Moment Diagram for the beam shown in Fig.1. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forward
- Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the Slope Deflection method. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forwardText Book Problem 7.82 (page 261) Consider the total head-loss in the system forthis flow is 18.56 ft (head-losses in first and second pipe are 13.83 ft and 4.73 ftrespectively). Please show numerical values for EGL/HGL at the beginning/end/intermediatechange point. (Point distribution: elevation determination 5 points, EGL, HGL lines 4points).(I think we are just using the values provided for head losses to solve this problem)arrow_forwardCalculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the moment distribution method, and draw the Shear force diagram and Bending moment diagram for the beam shown. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forward
- Calculate the BMs (bending moments) at all the joints of the beam shown in Fig.1 using the Slope deflection method. The beam is subjected to an UDL of w=65m. L=4.5m L1= 1.8m. Assume the support at C is pinned, and A and B are roller supports. E = 200GPa, I = 250x106 mm4.arrow_forwardThank you for your help if you would also provide the equations used .arrow_forwardThe sectors are divided as follows:top right = 1, top left = 2, middle = 3, bottom = 4.(a) Determine the distance yˉ to the centroid of the beam’s cross-sectional area.Solve the next questions by building a table. (Table format Answers) (b) Determine the second moment of area (moment of inertia) about the x′ axis. (c) Determine the second moment of area (moment of inertia) about the y-axis.arrow_forward

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning





