Chapter 5, Problem 41Q

To determine

The diagram showing all possible transitions between the levels of an imaginary atom, having energy $\text{0}\text{eV,}\text{1}\text{eV}\text{and}\text{3}\text{eV}$, the energy and wavelength of the photon for each transition and the transitions involving the absorption or emission of visible light.

Answer to Problem 41Q

Solution:

The diagram representing all possible transitions is shown below. The wavelengths for the energy differences $\text{1,}\text{2}\text{and}\text{3}\text{eV}$ are 1240, 620 and 413 nm, respectively. The transitions involving absorption or emission of visible light are between the levels with energy $\text{0}\text{eV}\text{and}\text{3}\text{eV}$ and the levels with energy $\text{1}\text{eV}\text{and}\text{3}\text{eV}$, respectively.

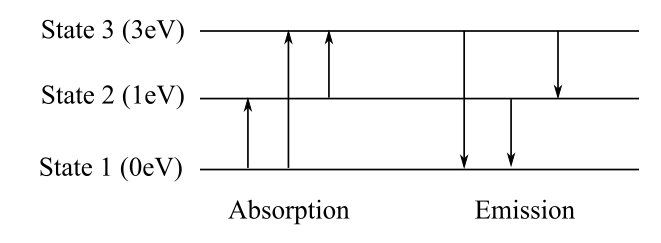
Explanation of Solution

Given data:

The energy values of the given atomic levels are $\text{0}\text{eV,}\text{1}\text{eV}\text{and}\text{3}\text{eV}$.

Formula used:

Planck’s quantum theory relates the energy difference between the transition levels to the frequency of the released radiation as:

$\Delta E=h\nu$

Or,

$\Delta E=\frac{hc}{\lambda }$

Here, $\lambda$ is the wavelength of electromagnetic wave.

Explanation:

The given atom has only three energy levels. Let, state 1 represents the level with energy $\text{0}\text{eV}$, state 2 represents the level with energy $\text{1}\text{eV}$ and state 3 represent the level with energy $\text{3}\text{eV}$.

Write the expression relating the energy and wavelength of the photon:

$\Delta E=\frac{hc}{\lambda }$

Here, $\Delta E\left(E_1-E_2\right)$ is the energy difference of the transition levels, $h$ is Planck’s constant and $c$ is the speed of light.

Estimate the energy difference of the levels.

The difference between first two energy states is,

$\begin{array}{c}\Delta E_1=\left(1-0\right)\text{eV}\\ \text{=}\text{1}\text{eV}\end{array}$

Similarly,

$\Delta E_2=2\text{eV}$

And,

$\Delta E_3=3\text{eV}$

Rewrite the above expression for energy difference for wavelength.

$\lambda =\frac{hc}{\Delta E}$

Substitute $4.136\times {10}^{-15}\text{eVs}$ for $h$ and $3\times {10}^{17}{\text{nms}}^{-1}$ for $c$.

$\begin{array}{c}\lambda =\frac{4.136\times {10}^{-15}\text{eVs}\times 3\times {10}^{17}{\text{nms}}^{-1}}{\Delta E}\\ =\frac{1240}{\Delta E}\text{nm}\end{array}$

Substitute $\text{1}\text{eV,}\text{3}\text{eV}\text{and}\text{2}\text{eV}$ for $\Delta E$ to get the wavelength for respective transitions.

${\lambda }_1=1240\text{nm}$, ${\lambda }_2=413\text{nm}$ and ${\lambda }_3=620\text{nm}$.

All the possible transitions are shown in the following diagram.

The absorption or emission transition of visible lights are between the states 2 and 3 and 1 and 3 as the wavelength for these transitions lie in the visible region.

Conclusion:

The energy level diagram is shown above. The values of energy of the photons are $\text{1}\text{eV,}\text{3}\text{eV}\text{and}\text{2}\text{eV}$ and the respective values of wavelength are 1240 nm, 413 nm and 620 nm. The absorption or emission transitions of visible light are between the levels with energy $\text{0}\text{eV}\text{and}\text{3}\text{eV}$ and the levels with energy $\text{1}\text{eV}\text{and}\text{3}\text{eV}$, respectively.