Chapter 5, Problem 1RE

In Exercises 1–8, find all the relative and absolute extrema of the given function on the given domain (if supplied) or on the largest possible domain (if no domain is supplied).

$f\left(x\right)=2x^3-6x+1\text{ on }\left[-2,+\infty \right]$

To determine

To calculate: The exact location of the relative and absolute extrema of the function $f\left(x\right)=2x^3-6x+1$ with domain $\left[-2,+\infty \right)$.

Answer to Problem 1RE

Solution:

The exact location of Absolute Minimum are $\left(1,-3\right)\text{ and }\left(-2,-3\right)$ and relative maximum at $\left(-1,5\right)$ of $f\left(x\right)=2x^3-6x+1$ with domain $\left[-2,+\infty \right)$.

Explanation of Solution

Given Information:

The provided equation is:

$f\left(x\right)=2x^3-6x+1$

Formula used:

First Derivative Test is, assume that for a critical point $c$ of the continuous function $f$, its derivative is defined for $x$ close to, and on both sides of $x=c$. Then, determine the sign of the derivative to the left and the right of $x=c$.

If $f\text{'}\left(x\right)$ is positive to the left of the point $x=c$ and negative to the right, then $f$ has a maximum at the point $x=c$.

If $f\text{'}\left(x\right)$ is negative to the left of the point $x=c$ and positive to the right, then $f$ has a minimum at the point $x=c$.

If $f\text{'}\left(x\right)$ has the same sign on both sides of the point $x=c$, then $f$ has neither a maximum nor a minimum at the point $x=c$.

Stationary Points are the points in the interior of the domain where the derivative is zero.

Singular Points are the points in the interior of the domain where the derivative is not defined.

Closed intervals contain end points which are the end points of the functions and the function does not have end points if the interval is open as open intervals do not have any end points.

Calculation:

Consider the provided equation:

$f\left(x\right)=2x^3-6x+1$

Differentiate both sides of the equation with respect to $x$.

$fg\text{'}\left(x\right)=6x^2-6$

Now, locate stationary points.

Recall that stationary Points are the points in the interior of the domain where the derivative is zero.

$\begin{array}{c}f\text{'}\left(x\right)=0\\ 6x^2-6=0\end{array}$

Adding $6$ to both sides of the equation to get:

$\begin{array}{c}6x^2-6+6=6\\ 6x^2=6\end{array}$

Multiplying both sides of the equation by $\frac{1}{6}$ to get:

$\begin{array}{c}6x^2\frac{1}{6}=6\frac{1}{6}\\ x^2=1\end{array}$

Taking square root of both sides of the equation to get:

$\begin{array}{c}\sqrt{x^2}=\sqrt{1}\\ x=\pm 1\end{array}$

The domain of the function is $\left[-2,+\infty \right)$, so $x=\pm 1$ is in the interior of the domain. Thus, the only candidate for a stationary relative extremum occurs when $x=\pm 1$

Now locate singular points.

Since $f\text{'}\left(x\right)$ is defined for all $x$ in the interior of the domain, so there are no singular points.

Next locate end points.

Since $\left[-2,+\infty \right)$ is the domain so the end point is $x=-2$.

The values of $x$ are recorded in a table, together with the corresponding $y-coordinates$(values of $f$).

$x$	$-2$	$-1$	$1$	$2$
$f\left(x\right)=2x^3-6x+1$	$-3$	5	$-3$	5

The graph increases from $x=-2$ until $x=-1$, then decreases until $x=1$ then increases again and beyond.

Use the above points to plot a graph

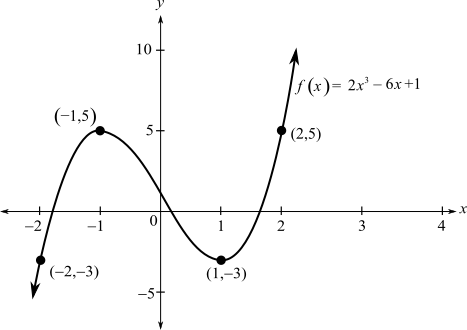
From figure we can see that $f$ has following extrema,

$x$	$f\left(x\right)=2x^3-6x+1$	Classification
$-2$	$-3$	Absolute Minimum
$1$	$-3$	Absolute Minimum
$-1$	$5$	Relative Maximum

Therefore, the exact location of Absolute Minimum are $\left(1,-3\right)\text{ and }\left(-2,-3\right)$ and relative maximum at $\left(-1,5\right)$ of $f\left(x\right)=2x^3-6x+1$ with domain $\left[-2,+\infty \right)$.