
(a)
To find: The expression for a Riemann sum of a function
(a)
Answer to Problem 1RCC
The expression for a Riemann sum of a function f is
Explanation of Solution
The Riemann sum of a function f is the method to find the total area underneath a curve.
The area under the curve dividedas n number of approximating rectangles. Hence the Riemann sum of a function f is the sum of the area of the all individual rectangles.
Here,
Thus, the expression for a Riemann sum of a function f is
b)
To define: The geometric interpretation of a Riemann sum with diagram.
b)
Explanation of Solution
Given information:
Consider the condition for the function
The function
Sketch the curve
Show the curve as in Figure 1.
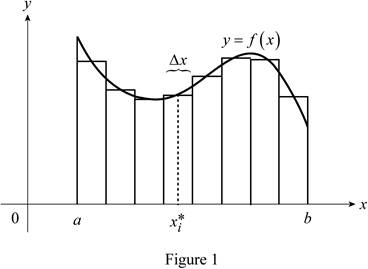
Refer to Figure 1
The function
Thus, the geometric interpretation of a Riemann sum of
c)
To define: The geometric interpretation of a Riemann sum, if the function
c)
Explanation of Solution
Given information:
The function
The function
Sketch the curve
Show the curve as in Figure 2.
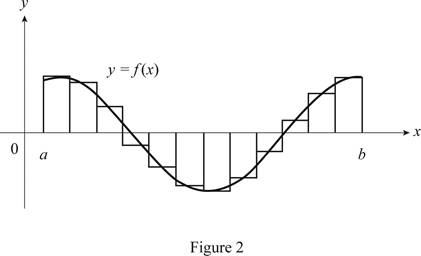
Refer figure 2,
The Riemann sum is the difference of areas of approximating rectangles above and below the x-axis
Therefore, the geometric interpretation of a Riemann sum is defined, if
Want to see more full solutions like this?
Chapter 5 Solutions
Student Solutions Manual for Stewart's Single Variable Calculus: Early Transcendentals, 8th (James Stewart Calculus)
- Find the interest earned on $10,000 invested for 6 years at 6% interest compounded as follows. a. Annually b. Semiannually (twice a year) c. Quarterly d. Monthly e. Continuouslyarrow_forward6.9x y= 100-x a. Find the cost of removing each percent of pollutants: 50%; 70%; 80%; 90%; 95%; 98%; 99%. 50% y = 70% y = 80% y = 90% YF 95% y = 98% y= 99% V =arrow_forwardThe cost per ton, y, to build an oil tanker of x thousand deadweight tons was approximated by 215,000 C(x)= x+485 C(25) C(100) C(300) =1 C(50) = = C(200) = C(400) =arrow_forward
- Prove that if a and b are both positive, then y(x)⭢0 as x⭢∞ for all sloutions y of the questionarrow_forwardShow how to use "Change of Variables Formula for Integrals" to solve "Separable Differential Equations"arrow_forwardUse the two methods "real number solution space basis" and "complex solution space basis" respectively to solve y''+ 4y' + 4y = 0, y(-1) = 2, y'(-1) = 1arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning  College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning



