
To Graph: a
Given: points are given in
Concept used:
(1) If a function
(2) A power model or function is defined as:
(4) An exponential model or function is as follows:
(5) Equation of a line passing through the given two points as like
Then,
Here,
Calculation:
(a)The table of data pairs
The Scatter graph of
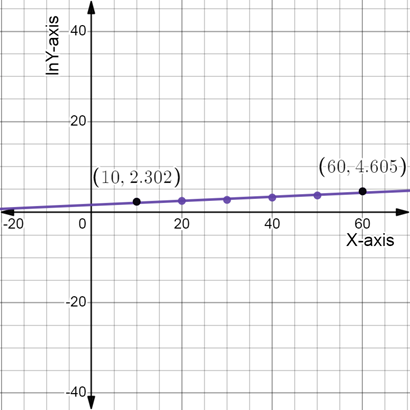
Here, choose two points
Now, substitute the value;
Thus,
Now, take the exponentiation of each side by e;
Therefore, the exponential function of the model is
(b)The table of data pairs
The Scatter graph of
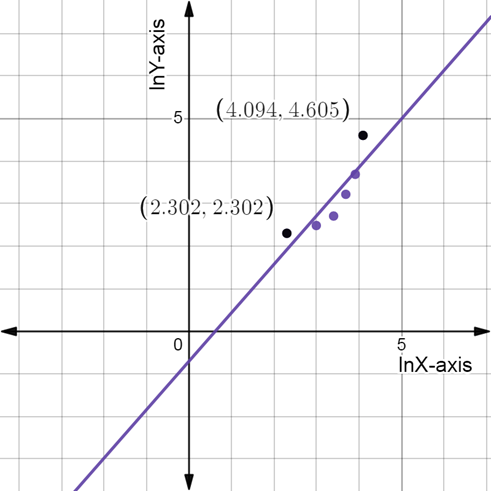
Here, choose two points
Now, substitute the value;
Thus,
Now, take the exponentiation of each side by e;
Therefore, the power function of the model is
(C) By the graph of an exponential function of the data pairs represents the straight line and generates the scatter plot. But the power function of the data pairs is not representing the scatter plot. So, the power function is not the original function.
Then also it is clear the exponential function of the model is perfect showing these points in a scatter plot.
(D)
An exponential model or function is as follows:
Therefore, the exponential function of the model is
Conclusion:
Hence, the exponential function of the model satisfies the given points be
Chapter 4 Solutions
Algebra 2: New York Edition (holt Mcdougal Larson Algebra 2)
- Can someone provide an answer & detailed explanation please? Thank you kindly!arrow_forwardGiven the cubic function f(x) = x^3-6x^2 + 11x- 6, do the following: Plot the graph of the function. Find the critical points and determine whether each is a local minimum, local maximum, or a saddle point. Find the inflection point(s) (if any).Identify the intervals where the function is increasing and decreasing. Determine the end behavior of the graph.arrow_forwardGiven the quadratic function f(x) = x^2-4x+3, plot the graph of the function and find the following: The vertex of the parabola .The x-intercepts (if any). The y-intercept. Create graph also before solve.arrow_forward
- what model best fits this dataarrow_forwardRound as specified A) 257 down to the nearest 10’s place B) 650 to the nearest even hundreds, place C) 593 to the nearest 10’s place D) 4157 to the nearest hundreds, place E) 7126 to the nearest thousand place arrow_forwardEstimate the following products in two different ways and explain each method  A) 52x39 B) 17x74 C) 88x11 D) 26x42arrow_forward
- Find a range estimate for these problems A) 57x1924 B) 1349x45 C) 547x73951arrow_forwardDraw the image of the following figure after a dilation centered at the origin with a scale factor of 14 退 14 12- 10 5- + Z 6 的 A X 10 12 14 16 18 G min 3 5arrow_forwardkofi makes a candle as a gift for his mom. The candle is a cube with a volume of 8/125 ft cubed. Kofi wants to paint each face of the candle exepct for the bottom. what is the area he will paint?arrow_forward
- 10 6 9. 8 -7- 6. 5. 4- 3. 2 1- -1 0 -1 2 3 4 ·10 5 6 7 00 8 6 10arrow_forwardWeek 3: Mortgages and Amortiza X + rses/167748/assignments/5379530?module_item_id=23896312 11:59pm Points 10 Submitting an external tool Gider the following monthly amortization schedule: Payment # Payment Interest Debt Payment Balance 1 1,167.34 540.54 626.80 259,873.20 2 1,167.34 539.24 628.10 259,245.10 3 1,167.34 With the exception of column one, all amounts are in dollars. Calculate the annual interest rate on this loa Round your answer to the nearest hundredth of a percent. Do NOT round until you calculate the final answer. * Previous a Earrow_forwardCafé Michigan's manager, Gary Stark, suspects that demand for mocha latte coffees depends on the price being charged. Based on historical observations, Gary has gathered the following data, which show the numbers of these coffees sold over six different price values: Price Number Sold $2.70 765 $3.50 515 $2.00 990 $4.30 240 $3.10 325 $4.00 475 Using simple linear regression and given that the price per cup is $1.85, the forecasted demand for mocha latte coffees will be cups (enter your response rounded to one decimal place).arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





