CALCULUS+ITS APPLICATIONS-MYMATHLAB
15th Edition
ISBN: 9780137590438
Author: Goldstein
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 4.4, Problem 40E
To determine
To prove: The graph of
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
15A cylindrical tank with radius 8 m is being filled with water at a rate of 2 m³/min.
What is the rate of change of the water height in this tank?
6)A box with a square base and an open top must
box that will minimi
#12 The radius of a sphere increases at a rate of 3 in/sec. How fast is the volume increasing when the diameter is 24
84 256 cubic inches. Find the dimensions of the
of material used (the surface area).
A farmer wishes to enclose a rectangular plot using 200 m of fencing material. One side of the land borders
a river and does not need fencing. What is the largest area that can be enclosed?
For the function y=x³-3x²-1, use derivatives to:
3
b) 2x
-
6x2
(a) determine the int
Chapter 4 Solutions
CALCULUS+ITS APPLICATIONS-MYMATHLAB
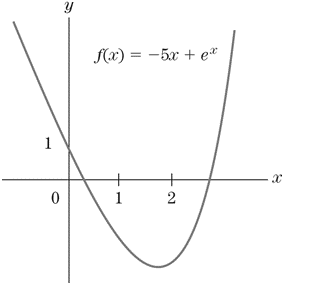
Ch. 4.1 - Can a function such as f(x)=53x be written in the...Ch. 4.1 - Solve the equation 7263x=28.Ch. 4.1 - Prob. 1ECh. 4.1 - Prob. 2ECh. 4.1 - Write each expression in Exercises 1-14 in the...Ch. 4.1 - Write each expression in Exercises 1-14 in the...Ch. 4.1 - Write each expression in Exercises 1-14 in the...Ch. 4.1 - Write each expression in Exercises 1-14 in the...Ch. 4.1 - Prob. 7ECh. 4.1 - Write each expression in Exercises 1-14 in the...
Ch. 4.1 - Write each expression in Exercises 1-14 in the...Ch. 4.1 - Prob. 10ECh. 4.1 - Prob. 11ECh. 4.1 - Write each expression in Exercises 1-14 in the...Ch. 4.1 - Prob. 13ECh. 4.1 - Prob. 14ECh. 4.1 - Find a number b such that the function f(x)=32x...Ch. 4.1 - Find b so that 8x/3=bx for all x.Ch. 4.1 - Solve the following equations for x. 52x=52Ch. 4.1 - Solve the following equations for x. 10x=102Ch. 4.1 - Solve the following equations for x....Ch. 4.1 - Solve the following equations for x....Ch. 4.1 - Solve the following equations for x. 101x=100Ch. 4.1 - Solve the following equations for x. 24x=8Ch. 4.1 - Solve the following equations for x. 3(2.7)5x=8.1Ch. 4.1 - Solve the following equations for x....Ch. 4.1 - Solve the following equations for x. (2x+123)2=2Ch. 4.1 - Solve the following equations for x. (32x32)4=3Ch. 4.1 - Solve the following equations for x. 23x=425xCh. 4.1 - Solve the following equations for x. 35x3x3=0Ch. 4.1 - Solve the following equations for x. (1+x)2x52x=0Ch. 4.1 - Prob. 30ECh. 4.1 - Solve the following equations for x. 2x822x=0Ch. 4.1 - Prob. 32ECh. 4.1 - Solve the following equations for x. [Hint: In...Ch. 4.1 - Prob. 34ECh. 4.1 - Solve the following equations for x. [Hint: In...Ch. 4.1 - Prob. 36ECh. 4.1 - The expressions in Exercises 37-42 may be factored...Ch. 4.1 - The expressions in Exercises 37-42 may be factored...Ch. 4.1 - The expressions in Exercises 37-42 may be factored...Ch. 4.1 - The expressions in Exercises 37-42 may be factored...Ch. 4.1 - The expressions in Exercises 37-42 may be factored...Ch. 4.1 - Prob. 42ECh. 4.1 - Prob. 43ECh. 4.1 - Prob. 44ECh. 4.1 - Prob. 45ECh. 4.2 - Solve the following equation for x: e6x=e3.Ch. 4.2 - Differentiate y=(x+ex)4Ch. 4.2 - Show that ddx(3x)|x=01.1 by calculating the slope...Ch. 4.2 - Show that ddx(2.7x)|x=0.99 by calculating the...Ch. 4.2 - In Exercises 3-6, compute the given derivatives...Ch. 4.2 - Prob. 4ECh. 4.2 - Prob. 5ECh. 4.2 - Prob. 6ECh. 4.2 - Write each expression in the form ekx for a...Ch. 4.2 - Write each expression in the form ekx for a...Ch. 4.2 - Write each expression in the form ekx for a...Ch. 4.2 - Write each expression in the form ekx for a...Ch. 4.2 - Write each expression in the form ekx for a...Ch. 4.2 - Prob. 12ECh. 4.2 - Solve each equation for x. e5x=e20Ch. 4.2 - Prob. 14ECh. 4.2 - Solve each equation for x. ex22x=e8Ch. 4.2 - Prob. 16ECh. 4.2 - Solve each equation for x. ex(x21)=0Ch. 4.2 - Solve each equation for x. 4ex(x2+1)=0Ch. 4.2 - Find an equation of the tangent line to the graph...Ch. 4.2 - Prob. 20ECh. 4.2 - Use the first and second derivative rules from...Ch. 4.2 - Prob. 22ECh. 4.2 - Suppose that A=(a,b) is a point on the graph of...Ch. 4.2 - Find the slope-point form of the equation of the...Ch. 4.2 - Differentiate the following functions. y=3ex7xCh. 4.2 - Differentiate the following functions. y=2x+45ex4Ch. 4.2 - Differentiate the following functions. y=xexCh. 4.2 - Differentiate the following functions....Ch. 4.2 - Differentiate the following functions....Ch. 4.2 - Differentiate the following functions....Ch. 4.2 - Differentiate the following functions. y=exx+1Ch. 4.2 - Prob. 32ECh. 4.2 - Differentiate the following functions. y=ex1ex+1Ch. 4.2 - Differentiate the following functions. y=ex+1Ch. 4.2 - The graph of y=xex has one extreme point. Find its...Ch. 4.2 - Prob. 36ECh. 4.2 - Find the point on the graph of y=(1+x2)ex where...Ch. 4.2 - Prob. 38ECh. 4.2 - Find the slope of the tangent line to the curve...Ch. 4.2 - Find the slope of the tangent line to the curve...Ch. 4.2 - Find the equation of the tangent line to the curve...Ch. 4.2 - Find the equation of the tangent line to the curve...Ch. 4.2 - Find the first and second derivatives....Ch. 4.2 - Find the first and second derivatives. f(x)=exxCh. 4.2 - Compute the following derivatives. ddx(5ex)...Ch. 4.2 - Prob. 46ECh. 4.2 - Prob. 47ECh. 4.2 - Prob. 48ECh. 4.2 - Prob. 49ECh. 4.2 - Prob. 50ECh. 4.2 - Prob. 51ECh. 4.2 - Prob. 52ECh. 4.2 - Prob. 53ECh. 4.2 - Prob. 54ECh. 4.2 - Prob. 55ECh. 4.2 - Prob. 56ECh. 4.3 - Differentiate tet2Ch. 4.3 - Differentiate [ e3x(1+e6x) ]12.Ch. 4.3 - Differentiate the following functions. f(x)=e2x+3Ch. 4.3 - Differentiate the following functions. f(x)=e3x2Ch. 4.3 - Differentiate the following functions. f(x)=e4x2xCh. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions. f(x)=eexCh. 4.3 - Differentiate the following functions. f(x)=e1xCh. 4.3 - Differentiate the following functions. f(x)=exCh. 4.3 - Differentiate the following functions. f(x)=ex2+1Ch. 4.3 - Differentiate the following functions. f(x)=7ex7Ch. 4.3 - Differentiate the following functions. f(x)=10ex25Ch. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions. f(x)=eeexCh. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions....Ch. 4.3 - Differentiate the following functions. f(x)=ex+1Ch. 4.3 - Differentiate the following functions. f(x)=eexCh. 4.3 - In Exercises 21-26, simplify the function before...Ch. 4.3 - In Exercises 21-26, simplify the function before...Ch. 4.3 - In Exercises 21-26, simplify the function before...Ch. 4.3 - In Exercises 21-26, simplify the function before...Ch. 4.3 - In Exercises 21-26, simplify the function before...Ch. 4.3 - In Exercises 21-26, simplify the function before...Ch. 4.3 - In Exercises 27-32, find the values of x at which...Ch. 4.3 - In Exercises 27-32, find the values of x at which...Ch. 4.3 - In Exercises 27-32, find the values of x at which...Ch. 4.3 - In Exercises 27-32, find the values of x at which...Ch. 4.3 - In Exercises 27-32, find the values of x at which...Ch. 4.3 - In Exercises 27-32, find the values of x at which...Ch. 4.3 - An Investment Portfolio The value of an investment...Ch. 4.3 - Depreciation of Assets The value of the computer t...Ch. 4.3 - The Most Expensive Artwork to Date The highest...Ch. 4.3 - Appreciation of Assets A painting purchased in...Ch. 4.3 - Velocity and Acceleration The velocity of the...Ch. 4.3 - Velocity and Acceleration Suppose the velocity of...Ch. 4.3 - Heights of a Plant The height of a certain plant,...Ch. 4.3 - Heights of a Plant The length of a certain weed,...Ch. 4.3 - Gompertz Growth Curve Let aandb be positive...Ch. 4.3 - Find dydx if y=e(110)ex2.Ch. 4.3 - Size of Tumor In a study, a cancerous tumor was...Ch. 4.3 - Height of a Plant Let f(t) be the function from...Ch. 4.4 - Find lne.Ch. 4.4 - Solve e3x=2 using the natural logarithm function.Ch. 4.4 - Find ln(e).Ch. 4.4 - Find ln(1e2).Ch. 4.4 - If ex=5, Write x in terms of the natural...Ch. 4.4 - If ex=3.2, Write x in terms of the natural...Ch. 4.4 - If lnx=1, Write x using the exponential function.Ch. 4.4 - If lnx=4.5, Write x using the exponential...Ch. 4.4 - Simplify the following expression. lne3Ch. 4.4 - Simplify the following expression. eln4.1Ch. 4.4 - Simplify the following expression. eeln1Ch. 4.4 - Simplify the following expression. ln(e2lne)Ch. 4.4 - Simplify the following expression. ln(lne)Ch. 4.4 - Simplify the following expression. e4ln1Ch. 4.4 - Simplify the following expression. e2lnxCh. 4.4 - Simplify the following expression. exln2Ch. 4.4 - Simplify the following expression. e2ln7Ch. 4.4 - Simplify the following expression. e2ln7Ch. 4.4 - Simplify the following expression. elnx+ln2Ch. 4.4 - Simplify the following expression. eln32lnxCh. 4.4 - Solve the following equations for x. e2x=5Ch. 4.4 - Solve the following equations for x. e13x=4Ch. 4.4 - Solve the following equations for x. ln(4x)=12Ch. 4.4 - Prob. 22ECh. 4.4 - Solve the following equations for x. lnx2=9Ch. 4.4 - Prob. 24ECh. 4.4 - Solve the following equations for x. 6e0.00012x=3Ch. 4.4 - Prob. 26ECh. 4.4 - Solve the following equations for x. ln3x=ln5Ch. 4.4 - Prob. 28ECh. 4.4 - Solve the following equations for x. ln(ln3x)=0Ch. 4.4 - Prob. 30ECh. 4.4 - Solve the following equations for x. 2ex/39=0Ch. 4.4 - Prob. 32ECh. 4.4 - Prob. 33ECh. 4.4 - Prob. 34ECh. 4.4 - Prob. 35ECh. 4.4 - Prob. 36ECh. 4.4 - Solve the following equations for x. 4exe2x=6Ch. 4.4 - Prob. 38ECh. 4.4 - The graph of f(x)=5x+ex is shown in fig. 4. Find...Ch. 4.4 - Prob. 40ECh. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Find the x-intercept of y=(x1)2ln(x+1),x1.Ch. 4.4 - In Exercise 45- 46, find the coordinates of each...Ch. 4.4 - In Exercise 45- 46, find the coordinates of each...Ch. 4.4 - Solve for t. e0.05t4e0.06t=0Ch. 4.4 - Solve for t. 4e0.01t3e0.04t=0Ch. 4.4 - Prob. 49ECh. 4.4 - Wind Velocity Under certain geographic conditions,...Ch. 4.4 - Prob. 51ECh. 4.4 - Prob. 52ECh. 4.4 - Prob. 53ECh. 4.4 - Prob. 54ECh. 4.4 - Prob. 55ECh. 4.5 - Differentiate f(x)=1ln(x4+5).Ch. 4.5 - Differentiate f(x)=ln(lnx).Ch. 4.5 - Prob. 3CYUCh. 4.5 - Differentiate the following functions. y=3lnx+ln2Ch. 4.5 - Differentiate the following functions. y=lnxln3Ch. 4.5 - Differentiate the following functions. y=x2lnx2Ch. 4.5 - Differentiate the following functions. y=3lnxxCh. 4.5 - Differentiate the following functions. y=exlnxCh. 4.5 - Differentiate the following functions. y=e1+lnxCh. 4.5 - Differentiate the following functions. y=lnxxCh. 4.5 - Prob. 8ECh. 4.5 - Differentiate the following functions. y=lnx2Ch. 4.5 - Prob. 10ECh. 4.5 - Differentiate the following functions. y=ln(1x)Ch. 4.5 - Prob. 12ECh. 4.5 - Differentiate the following functions. y=ln(3x4x2)Ch. 4.5 - Prob. 14ECh. 4.5 - Differentiate the following functions. y=1lnxCh. 4.5 - Differentiate the following functions. y=lnxln2xCh. 4.5 - Differentiate the following functions. y=lnxln2xCh. 4.5 - Differentiate the following functions. y=(lnx)2Ch. 4.5 - Differentiate the following functions....Ch. 4.5 - Differentiate the following functions....Ch. 4.5 - Find the second derivatives. d2dt2(t2lnt)Ch. 4.5 - Find the second derivatives. d2dt2ln(lnt)Ch. 4.5 - The graph of f(x)=(lnx)/x is shown in Fig.4. Find...Ch. 4.5 - The graph of f(x)=x/(lnx+x) is shown in Fig.5....Ch. 4.5 - Write the equation of the tangent line to the...Ch. 4.5 - The function f(x)=(lnx+1)/x has a relative extreme...Ch. 4.5 - Determine the domain of definition of the given...Ch. 4.5 - Find the equations of the tangent lines to the...Ch. 4.5 - Find the coordinates of the relative extreme point...Ch. 4.5 - Repeat the previous exercise with y=xlnx.Ch. 4.5 - The graphs of y=x+lnx and y=ln2x are shown in...Ch. 4.5 - Prob. 32ECh. 4.5 - Prob. 33ECh. 4.5 - The function y=2x2ln4x (x0) has one minimum point....Ch. 4.5 - A Demand Equation If the demand equation for a...Ch. 4.5 - Total Revenue Suppose that the total revenue...Ch. 4.5 - An Area ProblemFind the maximum area of a...Ch. 4.5 - Analysis of the Effectiveness of an Insect...Ch. 4.6 - Differentiate f(x)=ln[ exx(x+1)6 ].Ch. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Simplify the following expressions. ln5+lnxCh. 4.6 - Simplify the following expressions. lnx5lnx3Ch. 4.6 - Simplify the following expressions. 12ln9Ch. 4.6 - Simplify the following expressions. 3ln12+ln16Ch. 4.6 - Simplify the following expressions. ln4+ln6ln12Ch. 4.6 - Simplify the following expressions. ln2lnx+ln3Ch. 4.6 - Simplify the following expressions. e2lnxCh. 4.6 - Simplify the following expressions. 32ln45ln2Ch. 4.6 - Simplify the following expressions. 5lnx12lny+3lnzCh. 4.6 - Simplify the following expressions. elnx2+3lnyCh. 4.6 - Simplify the following expressions. lnxlnx2+lnx4Ch. 4.6 - Prob. 12ECh. 4.6 - Simplify the following expressions. Which is...Ch. 4.6 - Simplify the following expressions. Which is...Ch. 4.6 - Evaluate the given expressions. Use ln2=.69 and...Ch. 4.6 - Evaluate the given expressions. Use ln2=.69 and...Ch. 4.6 - Evaluate the given expressions. Use ln2=.69 and...Ch. 4.6 - Prob. 18ECh. 4.6 - Which of the following is the same as 4ln2x? a....Ch. 4.6 - Prob. 20ECh. 4.6 - Which of the following is the same as ln8x2ln2x?...Ch. 4.6 - Which of the following is the same as ln9x2? a....Ch. 4.6 - Solve the given equation for x. lnxlnx2+ln3=0Ch. 4.6 - Solve the given equation for x. lnx2ln3=0Ch. 4.6 - Solve the given equation for x. lnx42lnx=1Ch. 4.6 - Solve the given equation for x. lnx2ln2x+1=0Ch. 4.6 - Solve the given equation for x. (lnx)21=0Ch. 4.6 - Solve the given equation for x. 3lnxln3x=0Ch. 4.6 - Solve the given equation for x. lnx=lnxCh. 4.6 - Solve the given equation for x. 2(lnx)2+lnx1=0Ch. 4.6 - Solve the given equation for x. ln(x+1)ln(x2)=1Ch. 4.6 - Solve the given equation for x....Ch. 4.6 - Differentiate. y=ln[(x+5)(2x1)(4x)]Ch. 4.6 - Differentiate. y=ln[(x+1)(2x+1)(3x+1)]Ch. 4.6 - Differentiate. y=ln[(1+x)2(2+x)3(3+x)4]Ch. 4.6 - Differentiate. y=ln[e2x(x3+1)(x4+5x)]Ch. 4.6 - Differentiate. y=ln[xex2+1]Ch. 4.6 - Prob. 38ECh. 4.6 - Differentiate. y=ln(x+1)4ex1Ch. 4.6 - Differentiate. y=ln(x+1)4(x3+2)x1Ch. 4.6 - Prob. 41ECh. 4.6 - Prob. 42ECh. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Prob. 47ECh. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Use logarithmic differentiation to differentiate...Ch. 4.6 - Prob. 51ECh. 4.6 - Prob. 52ECh. 4.6 - Prob. 53ECh. 4.6 - Prob. 54ECh. 4 - State as many laws of exponents as you can recall.Ch. 4 - Prob. 2FCCECh. 4 - Prob. 3FCCECh. 4 - Prob. 4FCCECh. 4 - Prob. 5FCCECh. 4 - Prob. 6FCCECh. 4 - Prob. 7FCCECh. 4 - Prob. 8FCCECh. 4 - Prob. 9FCCECh. 4 - Prob. 10FCCECh. 4 - Prob. 11FCCECh. 4 - Prob. 12FCCECh. 4 - Prob. 13FCCECh. 4 - Prob. 14FCCECh. 4 - Calculate the following. 274/3Ch. 4 - Calculate the following. 41.5Ch. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Calculate the following. (25/7)14/5Ch. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Calculate the following. 40.240.3Ch. 4 - Simplify the following. (ex2)3Ch. 4 - Simplify the following. e5xe2xCh. 4 - Simplify the following. e3xexCh. 4 - Simplify the following. 2x3xCh. 4 - Simplify the following. (e8x+7e2x)e3xCh. 4 - Simplify the following. e5x/2e3xexCh. 4 - Solve the following equations for x. e3x=e12Ch. 4 - Solve the following equations for x. ex2x=e2Ch. 4 - Solve the following equations for x. (exe2)3=e9Ch. 4 - Solve the following equations for x. e5xe4=eCh. 4 - Differntiate the following functions. y=10e7xCh. 4 - Differntiate the following functions. y=exCh. 4 - Differentiate the following functions. y=xex2Ch. 4 - Differentiate the following functions. y=ex+1x1Ch. 4 - Differntiate the following functions. y=eexCh. 4 - Differntiate the following functions. y=(x+1)e2xCh. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions. y=xeCh. 4 - The graph of the functions f(x)=ex24x2 is shown in...Ch. 4 - Show that the function in Fig. 1 has a relative...Ch. 4 - Solve the following equations for t....Ch. 4 - Solve the following equations for t. et8e0.02t=0Ch. 4 - Solve the equation 42x=ex. [Hint: Express 2x as an...Ch. 4 - Solve the equation 3x=2ex. [Hint: Express 3x as an...Ch. 4 - Find the points on the graph of y=ex where the...Ch. 4 - Find the points on the graph y=ex+e2x where the...Ch. 4 - Determine the intervals where the function...Ch. 4 - Determine the intervals where the function...Ch. 4 - Find the equation of the tangent line to the graph...Ch. 4 - Show that the tangent lines to the graph of...Ch. 4 - Simplify the following expressions. e(ln5)/2Ch. 4 - Simplify the following expressions. eln(x2)Ch. 4 - Simplify the following expressions. lnx2lnx3Ch. 4 - Simplify the following expressions. e2ln2Ch. 4 - Simplify the following expressions. e5ln1Ch. 4 - Simplify the following expressions. [elnx]2Ch. 4 - Solve the following equations for t. tlnt=eCh. 4 - Solve the following equations for t. ln(ln3t)=0Ch. 4 - Solve the following equations for t. 3e2t=15Ch. 4 - Solve the following equations for t. 3et/212=0Ch. 4 - Solve the following equations for t. 2lnt=5Ch. 4 - Solve the following equations for t. 2e0.3t=1Ch. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions. y=xlnxCh. 4 - Differentiate the following functions. y=ln(5x7)Ch. 4 - Differentiate the following functions. y=ln(9x)Ch. 4 - Differentiate the following functions. y=(lnx)2Ch. 4 - Differentiate the following functions. y=(xlnx)3Ch. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions. y=xlnxxCh. 4 - Differentiate the following functions. y=e2ln(x+1)Ch. 4 - Differentiate the following functions. y=ln(lnx)Ch. 4 - Differentiate the following functions. y=1lnxCh. 4 - Differentiate the following functions. y=exlnxCh. 4 - Differentiate the following functions. y=ln(x2+ex)Ch. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions. y=ln|2x+1|Ch. 4 - Differentiate the following functions. y=ln(ex2x)Ch. 4 - Differentiate the following functions. y=lnx3+3x23Ch. 4 - Differentiate the following functions. y=ln(2x)Ch. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions. y=ln|x1|Ch. 4 - Differentiate the following functions....Ch. 4 - Differentiate the following functions. y=ln(1ex)Ch. 4 - Differentiate the following functions....Ch. 4 - Use logarithmic differentiation to differentiate...Ch. 4 - Use logarithmic differentiation to differentiate...Ch. 4 - Use logarithmic differentiation to differentiate...Ch. 4 - Use logarithmic differentiation to differentiate...Ch. 4 - Use logarithmic differentiation to differentiate...Ch. 4 - Prob. 80RECh. 4 - Prob. 81RECh. 4 - Prob. 82RECh. 4 - Use logarithmic differentiation to differentiate...Ch. 4 - Prob. 84RECh. 4 - Prob. 85RECh. 4 - Prob. 86RECh. 4 - Prob. 87RECh. 4 - Health Expenditures The health expenditures (in...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Can you solve this 6 questions numerical method and teach me how to solve it and what we use.arrow_forward9Wire of length 20m is divided into two pieces and the pieces are bent into a square and a circle. How should this be done in order to minimize the sum of their areas? Round your answer to the nearest hundredth.arrow_forwardUse Laplace transform to solve the initial value problem y' + y = tsin(t), y(0) = 0arrow_forward
- The function g is defined by g(x) = sec² x + tan x. What are all solutions to g(x) = 1 on the interval 0 ≤ x ≤ 2π ? A x = = 0, x == = 3, x = π, x = 7 4 , 4 and x 2π only = B x = 4' 1, x = 1, x = 57 and x = 3 only C x = πk and x = - +πk D , where is any integer П x = +πk and П x = +πk, where k is any integerarrow_forwardVector v = PQ has initial point P (2, 14) and terminal point Q (7, 3). Vector v = RS has initial point R (29, 8) and terminal point S (12, 17). Part A: Write u and v in linear form. Show all necessary work. Part B: Write u and v in trigonometric form. Show all necessary work. Part C: Find 7u − 4v. Show all necessary calculations.arrow_forwardAn object is suspended by two cables attached at a single point. The force applied on one cable has a magnitude of 125 pounds and acts at an angle of 37°. The force on the other cable is 75 pounds at an angle of 150°.Part A: Write each vector in component form. Show all necessary work.Part B: Find the dot product of the vectors. Show all necessary calculations Part C: Use the dot product to find the angle between the cables. Round the answer to the nearest degree. Show all necessary calculations.arrow_forward
- An airplane flies at 500 mph with a direction of 135° relative to the air. The plane experiences a wind that blows 60 mph with a direction of 60°.Part A: Write each of the vectors in linear form. Show all necessary calculations.Part B: Find the sum of the vectors. Show all necessary calculations. Part C: Find the true speed and direction of the airplane. Round the speed to the thousandths place and the direction to the nearest degree. Show all necessary calculations.arrow_forwardUse sigma notation to write the sum. Σ EM i=1 - n 2 4n + n narrow_forwardVectors t = 3i + 7j, u = 2i − 5j, and v = −21i + 9j are given.Part A: Find the angle between vectors t and u. Show all necessary calculations. Part B: Choose a value for c, such that c > 1. Find w = cv. Show all necessary work.Part C: Use the dot product to determine if t and w are parallel, orthogonal, or neither. Justify your answer.arrow_forward
- A small company of science writers found that its rate of profit (in thousands of dollars) after t years of operation is given by P'(t) = (5t + 15) (t² + 6t+9) ³. (a) Find the total profit in the first three years. (b) Find the profit in the sixth year of operation. (c) What is happening to the annual profit over the long run? (a) The total profit in the first three years is $ (Round to the nearest dollar as needed.)arrow_forwardFind the area between the curves. x= -2, x = 7, y=2x² +3, y=0 Set up the integral (or integrals) needed to compute this area. Use the smallest possible number of integrals. Select the correct choice below and fill in the answer boxes to complete your choice. A. 7 [[2x² +3] dx -2 B. [[ ] dx+ -2 7 S [ ] dx The area between the curves is (Simplify your answer.)arrow_forwardThe rate at which a substance grows is given by R'(x) = 105e0.3x, where x is the time (in days). What is the total accumulated growth during the first 2.5 days? Set up the definite integral that determines the accumulated growth during the first 2.5 days. 2.5 Growth = (105e0.3x) dx 0 (Type exact answers in terms of e.) Evaluate the definite integral. Growth= (Do not round until the final answer. Then round to one decimal place as needed.)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Implicit Differentiation Explained - Product Rule, Quotient & Chain Rule - Calculus; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=LGY-DjFsALc;License: Standard YouTube License, CC-BY