EBK INTERMEDIATE ALGEBRA FOR COLLEGE ST
EBK INTERMEDIATE ALGEBRA FOR COLLEGE ST
8th Edition
ISBN: 9780136553632
Author: Blitzer
Publisher: VST
bartleby

Concept explainers

Equations and Inequations
Equations and inequalities describe the relationship between two mathematical expressions.
Linear Functions
A linear function can just be a constant, or it can be the constant multiplied with the variable like x or y. If the variables are of the form, x2, x1/2 or y2 it is not linear. The exponent over the variables should always be 1.
bartleby

Videos

Textbook Question
Book Icon
Chapter 4.2, Problem 70ES

Application Exercises

In more U.S. marriages, spouses have different faiths. The bar graph shows the percentage of households with an interfaith marriage in 1988 and 2012. Also shown is the percentage of households in which a person of faith is married to someone with no religion.

Percentage of U.S. Households in which Married

Couples Do Not Share the Same Faith

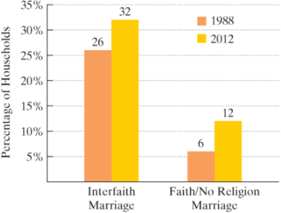
Chapter 4.2, Problem 70ES, Application Exercises In more U.S. marriages, spouses have different faiths. The bar graph shows the

Source: General Social Survey, University of Chicago

The formula

I = 1 4 x + 26

models the percentage of U.S. households with an interfaith marriage, I, x years after 1988. The formula

N = 1 4 x + 6

models the percentage of U.S. households in which a person of faith is married to someone with no religion, N, x years after 1988. Use theses modes to solve Exercises 69 – 70.

a. In which years will more than 34% of U.S. households have an interfaith marriage?

b. In which years will more than 15% of U.S. households have a person of faith married to someone with no religion?

c. Based on your answers to parts (a) and (b), in which years will more than 34% of households have an interfaith marriage and more than 15% have a faith/no religion marriage?

d. Based on your answers to parts (a) and (b), in which years will more than 34% of households have an interfaith marriage or more than 15% have a faith/no religion marriage?

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 4.2, Problem 69ES
Next
Chapter 4.2, Problem 71ES
Students have asked these similar questions
20 2. Let A = = [ -2 0 1 3 ] and B = 2 3 -1 2 For each of the following, calculate the product or indicate why it is undefined: (a) AB (b) BA
Answer the number questions with the following answers  +/- 2 sqrt(2) +/- i sqrt(6) (-3 +/-3 i sqrt(3))/4 +/-1 +/- sqrt(6) +/- 2/3 sqrt(3) 4 -3 +/- 3 i sqrt(3)
1 Matching 10 points Factor and Solve 1)x3-216 0, x = {6,[B]} 2) 16x3 = 54 x-[3/2,[D]] 3)x4x2-42 0 x= [ +/-isqrt(7), [F] } 4)x+3-13-9x x=[+/-1.[H]] 5)x38x2+16x=0, x = {0,[K}} 6) 2x6-10x-48x2-0 x-[0, [M], +/-isqrt(3)) 7) 3x+2x²-8 x = {+/-i sqrt(2), {Q}} 8) 5x³-3x²+32x=2x+18 x = {3/5, [S]} [B] [D] [F] [H] [K] [M] [Q] +/-2 sqrt(2) +/- i sqrt(6) (-3+/-3 i sqrt(3))/4 +/- 1 +/-sqrt(6) +/- 2/3 sqrt(3) 4 -3 +/- 3 i sqrt(3) [S]

Chapter 4 Solutions

EBK INTERMEDIATE ALGEBRA FOR COLLEGE ST

Ch. 4.1 - Check Point 1 Solve and graph the solution set on...Ch. 4.1 - Check Point 2 Solve and graph the solution set:...Ch. 4.1 - Prob. 3CPCh. 4.1 - Prob. 4CPCh. 4.1 - Prob. 5CPCh. 4.1 - Prob. 1CAVCCh. 4.1 - Prob. 2CAVCCh. 4.1 - Prob. 3CAVCCh. 4.1 - Prob. 4CAVCCh. 4.1 - Prob. 5CAVC
Ch. 4.1 - Prob. 6CAVCCh. 4.1 - Prob. 7CAVCCh. 4.1 - Prob. 8CAVCCh. 4.1 - Prob. 9CAVCCh. 4.1 - Prob. 10CAVCCh. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - Prob. 2ESCh. 4.1 - Prob. 3ESCh. 4.1 - Prob. 4ESCh. 4.1 - Prob. 5ESCh. 4.1 - Prob. 6ESCh. 4.1 - Prob. 7ESCh. 4.1 - Prob. 8ESCh. 4.1 - Prob. 9ESCh. 4.1 - Prob. 10ESCh. 4.1 - In Exercises 1 –32, solve each linear inequality....Ch. 4.1 - Prob. 12ESCh. 4.1 - Prob. 13ESCh. 4.1 - Prob. 14ESCh. 4.1 - In Exercises 1 –32, solve each linear inequality....Ch. 4.1 - Prob. 16ESCh. 4.1 - In Exercises 1 –32, solve each linear inequality....Ch. 4.1 - Prob. 18ESCh. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - Prob. 20ESCh. 4.1 - Prob. 21ESCh. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - Prob. 23ESCh. 4.1 - Prob. 24ESCh. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - Prob. 26ESCh. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - In Exercises 1 32, solve each linear inequality....Ch. 4.1 - Prob. 30ESCh. 4.1 - Prob. 31ESCh. 4.1 - Prob. 32ESCh. 4.1 - Prob. 33ESCh. 4.1 - Prob. 34ESCh. 4.1 - Prob. 35ESCh. 4.1 - Prob. 36ESCh. 4.1 - Prob. 37ESCh. 4.1 - Prob. 38ESCh. 4.1 - Prob. 39ESCh. 4.1 - Prob. 40ESCh. 4.1 - Prob. 41ESCh. 4.1 - Prob. 42ESCh. 4.1 - Prob. 43ESCh. 4.1 - Prob. 44ESCh. 4.1 - Prob. 45ESCh. 4.1 - Prob. 46ESCh. 4.1 - The graphs show that the three components of love,...Ch. 4.1 - Prob. 48ESCh. 4.1 - Prob. 49ESCh. 4.1 - Prob. 50ESCh. 4.1 - Prob. 51ESCh. 4.1 - Prob. 52ESCh. 4.1 - Prob. 53ESCh. 4.1 - Prob. 54ESCh. 4.1 - Diversity Index. What is the chance that the next...Ch. 4.1 - Prob. 56ESCh. 4.1 - Prob. 57ESCh. 4.1 - Prob. 58ESCh. 4.1 - Prob. 59ESCh. 4.1 - Prob. 60ESCh. 4.1 - A city commission has proposed two tax bills. The...Ch. 4.1 - Prob. 62ESCh. 4.1 - 63. A company manufactures and sells blank DVDs....Ch. 4.1 - Prob. 64ESCh. 4.1 - 65. An elevator at a construction site has a...Ch. 4.1 - Prob. 66ESCh. 4.1 - Prob. 67ESCh. 4.1 - Prob. 68ESCh. 4.1 - Prob. 69ESCh. 4.1 - Prob. 70ESCh. 4.1 - Prob. 71ESCh. 4.1 - Prob. 72ESCh. 4.1 - Prob. 73ESCh. 4.1 - Prob. 74ESCh. 4.1 - Prob. 75ESCh. 4.1 - Prob. 76ESCh. 4.1 - Prob. 77ESCh. 4.1 - Prob. 78ESCh. 4.1 - Prob. 79ESCh. 4.1 - Prob. 80ESCh. 4.1 - I have trouble remembering when to reverse the...Ch. 4.1 - Prob. 82ESCh. 4.1 - Prob. 83ESCh. 4.1 - Prob. 84ESCh. 4.1 - Prob. 85ESCh. 4.1 - Prob. 86ESCh. 4.1 - Prob. 87ESCh. 4.1 - Prob. 88ESCh. 4.1 - Prob. 89ESCh. 4.1 - Prob. 90ESCh. 4.1 - Prob. 91ESCh. 4.1 - Prob. 92ESCh. 4.1 - Prob. 93ESCh. 4.1 - Prob. 94ESCh. 4.1 - Prob. 95ESCh. 4.2 - Prob. 1CPCh. 4.2 - Prob. 2CPCh. 4.2 - Prob. 3CPCh. 4.2 - Prob. 4CPCh. 4.2 - Prob. 5CPCh. 4.2 - Prob. 6CPCh. 4.2 - Prob. 7CPCh. 4.2 - 1. The set of elements common to both set A and...Ch. 4.2 - Prob. 2CAVCCh. 4.2 - Prob. 3CAVCCh. 4.2 - Prob. 4CAVCCh. 4.2 - Prob. 5CAVCCh. 4.2 - Prob. 1ESCh. 4.2 - Prob. 2ESCh. 4.2 - Prob. 3ESCh. 4.2 - Prob. 4ESCh. 4.2 - Prob. 5ESCh. 4.2 - Prob. 6ESCh. 4.2 - Prob. 7ESCh. 4.2 - Prob. 8ESCh. 4.2 - Prob. 9ESCh. 4.2 - Prob. 10ESCh. 4.2 - In Exercises 7 – 24, solve each compound...Ch. 4.2 - In Exercises 7 – 24, solve each compound...Ch. 4.2 - Prob. 13ESCh. 4.2 - Prob. 14ESCh. 4.2 - Prob. 15ESCh. 4.2 - In Exercises 7 – 24, solve each compound...Ch. 4.2 - Prob. 17ESCh. 4.2 - Prob. 18ESCh. 4.2 - In Exercises 7 – 24, solve each compound...Ch. 4.2 - Prob. 20ESCh. 4.2 - Prob. 21ESCh. 4.2 - Prob. 22ESCh. 4.2 - Prob. 23ESCh. 4.2 - Prob. 24ESCh. 4.2 - In Exercises 25 – 32, solve each inequality and...Ch. 4.2 - Prob. 26ESCh. 4.2 - Prob. 27ESCh. 4.2 - Prob. 28ESCh. 4.2 - In Exercises 25 – 32, solve each inequality and...Ch. 4.2 - Prob. 30ESCh. 4.2 - In Exercises 25 – 32, solve each inequality and...Ch. 4.2 - Prob. 32ESCh. 4.2 - Prob. 33ESCh. 4.2 - Prob. 34ESCh. 4.2 - Prob. 35ESCh. 4.2 - Prob. 36ESCh. 4.2 - Prob. 37ESCh. 4.2 - Prob. 38ESCh. 4.2 - Prob. 39ESCh. 4.2 - In Exercises 39 54, solve each compound...Ch. 4.2 - In Exercises 39 – 54, solve each compound...Ch. 4.2 - Prob. 42ESCh. 4.2 - In Exercises 39 – 54, solve each compound...Ch. 4.2 - Prob. 44ESCh. 4.2 - In Exercises 39 54, solve each compound...Ch. 4.2 - Prob. 46ESCh. 4.2 - Prob. 47ESCh. 4.2 - Prob. 48ESCh. 4.2 - Prob. 49ESCh. 4.2 - In Exercises 39 – 54, solve each compound...Ch. 4.2 - In Exercises 39 54, solve each compound...Ch. 4.2 - Prob. 52ESCh. 4.2 - Prob. 53ESCh. 4.2 - Prob. 54ESCh. 4.2 - Prob. 55ESCh. 4.2 - Prob. 56ESCh. 4.2 - Prob. 57ESCh. 4.2 - Prob. 58ESCh. 4.2 - Prob. 59ESCh. 4.2 - Prob. 60ESCh. 4.2 - Prob. 61ESCh. 4.2 - Prob. 62ESCh. 4.2 - Prob. 63ESCh. 4.2 - Prob. 64ESCh. 4.2 - Prob. 65ESCh. 4.2 - Prob. 66ESCh. 4.2 - Prob. 67ESCh. 4.2 - Prob. 68ESCh. 4.2 - Application Exercises In more U.S. marriages,...Ch. 4.2 - Application Exercises In more U.S. marriages,...Ch. 4.2 - Prob. 71ESCh. 4.2 - Prob. 72ESCh. 4.2 - On the first four exams, your grades are 70, 75,...Ch. 4.2 - Prob. 74ESCh. 4.2 - Prob. 75ESCh. 4.2 - Parts for an automobile repair cost $1.75. The...Ch. 4.2 - Prob. 77ESCh. 4.2 - Prob. 78ESCh. 4.2 - Prob. 79ESCh. 4.2 - Prob. 80ESCh. 4.2 - Prob. 81ESCh. 4.2 - Prob. 82ESCh. 4.2 - Prob. 83ESCh. 4.2 - Prob. 84ESCh. 4.2 - Prob. 85ESCh. 4.2 - Prob. 86ESCh. 4.2 - Prob. 87ESCh. 4.2 - Prob. 88ESCh. 4.2 - Prob. 89ESCh. 4.2 - Prob. 90ESCh. 4.2 - Prob. 91ESCh. 4.2 - Prob. 92ESCh. 4.2 - Prob. 93ESCh. 4.2 - In Exercises 92 –95, determine whether each...Ch. 4.2 - Prob. 95ESCh. 4.2 - Prob. 96ESCh. 4.2 - Prob. 97ESCh. 4.2 - Prob. 98ESCh. 4.2 - Prob. 99ESCh. 4.2 - Prob. 100ESCh. 4.2 - Prob. 101ESCh. 4.2 - Prob. 102ESCh. 4.2 - Prob. 103ESCh. 4.2 - Prob. 104ESCh. 4.2 - Prob. 105ESCh. 4.2 - Prob. 106ESCh. 4.2 - Prob. 107ESCh. 4.3 - Prob. 1CPCh. 4.3 - Prob. 2CPCh. 4.3 - Prob. 3CPCh. 4.3 - Prob. 4CPCh. 4.3 - Prob. 5CPCh. 4.3 - Prob. 6CPCh. 4.3 - Prob. 7CPCh. 4.3 - Prob. 1CAVCCh. 4.3 - Prob. 2CAVCCh. 4.3 - Prob. 3CAVCCh. 4.3 - Prob. 4CAVCCh. 4.3 - Prob. 5CAVCCh. 4.3 - Prob. 6CAVCCh. 4.3 - Prob. 7CAVCCh. 4.3 - Prob. 8CAVCCh. 4.3 - Prob. 9CAVCCh. 4.3 - Prob. 10CAVCCh. 4.3 - Prob. 11CAVCCh. 4.3 - Prob. 12CAVCCh. 4.3 - Prob. 1ESCh. 4.3 - Prob. 2ESCh. 4.3 - Prob. 3ESCh. 4.3 - Prob. 4ESCh. 4.3 - Prob. 5ESCh. 4.3 - Prob. 6ESCh. 4.3 - Prob. 7ESCh. 4.3 - Prob. 8ESCh. 4.3 - Prob. 9ESCh. 4.3 - Prob. 10ESCh. 4.3 - Prob. 11ESCh. 4.3 - Prob. 12ESCh. 4.3 - In Exercises 1 – 38, find the solution set for...Ch. 4.3 - Prob. 14ESCh. 4.3 - Prob. 15ESCh. 4.3 - Prob. 16ESCh. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - Prob. 18ESCh. 4.3 - Prob. 19ESCh. 4.3 - Prob. 20ESCh. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - Prob. 22ESCh. 4.3 - Prob. 23ESCh. 4.3 - Prob. 24ESCh. 4.3 - Prob. 25ESCh. 4.3 - Prob. 26ESCh. 4.3 - In Exercises 1– 38, find the solution set for each...Ch. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - In Exercises 1– 38 , find the solution set for...Ch. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - In Exercises 1 38, find the solution set for each...Ch. 4.3 - In Exercises 1 – 38, find the solution set for...Ch. 4.3 - In Exercises 1– 38, find the solution set for each...Ch. 4.3 - Prob. 36ESCh. 4.3 - Prob. 37ESCh. 4.3 - Prob. 38ESCh. 4.3 - In Exercises 39 74, solve and graph the solution...Ch. 4.3 - In Exercises 39– 74, solve and graph the solution...Ch. 4.3 - In Exercises 39 74, solve and graph the solution...Ch. 4.3 - In Exercises 39– 74, solve and graph the solution...Ch. 4.3 - In Exercises 39 – 74, solve and graph the solution...Ch. 4.3 - Prob. 44ESCh. 4.3 - In Exercises 39 – 74, solve and graph the solution...Ch. 4.3 - In Exercises 39 74, solve and graph the solution...Ch. 4.3 - Prob. 47ESCh. 4.3 - Prob. 48ESCh. 4.3 - In Exercises 39– 74, solve and graph the solution...Ch. 4.3 - Prob. 50ESCh. 4.3 - Prob. 51ESCh. 4.3 - In Exercises 39 74, solve and graph the solution...Ch. 4.3 - Prob. 53ESCh. 4.3 - Prob. 54ESCh. 4.3 - In Exercises 39 74, solve and graph the solution...Ch. 4.3 - Prob. 56ESCh. 4.3 - Prob. 57ESCh. 4.3 - Prob. 58ESCh. 4.3 - Prob. 59ESCh. 4.3 - Prob. 60ESCh. 4.3 - Prob. 61ESCh. 4.3 - In Exercises 39 − 74, solve and graph the solution...Ch. 4.3 - In Exercises 39 −74, solve and graph the solution...Ch. 4.3 - Prob. 64ESCh. 4.3 - Prob. 65ESCh. 4.3 - Prob. 66ESCh. 4.3 - Prob. 67ESCh. 4.3 - Prob. 68ESCh. 4.3 - In Exercises 39 −74, solve and graph the solution...Ch. 4.3 - Prob. 70ESCh. 4.3 - Prob. 71ESCh. 4.3 - Prob. 72ESCh. 4.3 - In Exercises 39 74, solve and graph the solution...Ch. 4.3 - Prob. 74ESCh. 4.3 - Prob. 75ESCh. 4.3 - Prob. 76ESCh. 4.3 - 77. Let | and Find all values of x for which Ch. 4.3 - 78. Let and Find all values of x for which Ch. 4.3 - Prob. 79ESCh. 4.3 - Prob. 80ESCh. 4.3 - Let h(x)=|2x3|+1 Find all values of x for which...Ch. 4.3 - Prob. 82ESCh. 4.3 - Prob. 83ESCh. 4.3 - Prob. 84ESCh. 4.3 - Prob. 85ESCh. 4.3 - Prob. 86ESCh. 4.3 - In Exercises 87− 88, use the graph of to solve...Ch. 4.3 - Prob. 88ESCh. 4.3 - Prob. 89ESCh. 4.3 - Prob. 90ESCh. 4.3 - Prob. 91ESCh. 4.3 - Prob. 92ESCh. 4.3 - Prob. 93ESCh. 4.3 - Prob. 94ESCh. 4.3 - Prob. 95ESCh. 4.3 - Prob. 96ESCh. 4.3 - Prob. 97ESCh. 4.3 - Prob. 98ESCh. 4.3 - Prob. 99ESCh. 4.3 - Prob. 100ESCh. 4.3 - Prob. 101ESCh. 4.3 - Prob. 102ESCh. 4.3 - Prob. 103ESCh. 4.3 - Prob. 104ESCh. 4.3 - Prob. 105ESCh. 4.3 - Prob. 106ESCh. 4.3 - Prob. 107ESCh. 4.3 - Prob. 108ESCh. 4.3 - Prob. 109ESCh. 4.3 - Prob. 110ESCh. 4.3 - Prob. 111ESCh. 4.3 - Prob. 112ESCh. 4.3 - Prob. 113ESCh. 4.3 - Prob. 114ESCh. 4.3 - Prob. 115ESCh. 4.3 - Prob. 116ESCh. 4.3 - Prob. 117ESCh. 4.3 - Prob. 118ESCh. 4.3 - Prob. 119ESCh. 4.3 - Prob. 120ESCh. 4.3 - Prob. 121ESCh. 4.3 - Prob. 122ESCh. 4.3 - Prob. 123ESCh. 4.3 - Prob. 124ESCh. 4.3 - Prob. 125ESCh. 4.3 - Prob. 126ESCh. 4.3 - Prob. 127ESCh. 4.3 - Prob. 128ESCh. 4.3 - Prob. 1MCCPCh. 4.3 - Prob. 2MCCPCh. 4.3 - Prob. 3MCCPCh. 4.3 - Prob. 4MCCPCh. 4.3 - Prob. 5MCCPCh. 4.3 - Prob. 6MCCPCh. 4.3 - Prob. 7MCCPCh. 4.3 - In Exercises 1 – 18, solve each inequality or...Ch. 4.3 - Prob. 9MCCPCh. 4.3 - Prob. 10MCCPCh. 4.3 - Prob. 11MCCPCh. 4.3 - Prob. 12MCCPCh. 4.3 - Prob. 13MCCPCh. 4.3 - Prob. 14MCCPCh. 4.3 - Prob. 15MCCPCh. 4.3 - Prob. 16MCCPCh. 4.3 - Prob. 17MCCPCh. 4.3 - Prob. 18MCCPCh. 4.3 - Prob. 19MCCPCh. 4.3 - Prob. 20MCCPCh. 4.3 - Prob. 21MCCPCh. 4.3 - Prob. 22MCCPCh. 4.4 - Check point 1 Graph: Ch. 4.4 - Prob. 2CPCh. 4.4 - Check point 3 Graph each inequality in a...Ch. 4.4 - Check point 4 Show that point B in Figure 4.14 is...Ch. 4.4 - Prob. 5CPCh. 4.4 - Prob. 6CPCh. 4.4 - Prob. 1CAVCCh. 4.4 - Prob. 2CAVCCh. 4.4 - Prob. 3CAVCCh. 4.4 - Prob. 4CAVCCh. 4.4 - Prob. 5CAVCCh. 4.4 - Prob. 6CAVCCh. 4.4 - Prob. 7CAVCCh. 4.4 - Prob. 8CAVCCh. 4.4 - In Exercises 1 22, graph each inequality. x+y3Ch. 4.4 - Prob. 2ESCh. 4.4 - Prob. 3ESCh. 4.4 - Prob. 4ESCh. 4.4 - In Exercises1 – 22, graph each inequality. Ch. 4.4 - Prob. 6ESCh. 4.4 - Prob. 7ESCh. 4.4 - Prob. 8ESCh. 4.4 - In Exercises 1 22, graph each inequality. x2+y31Ch. 4.4 - Prob. 10ESCh. 4.4 - Prob. 11ESCh. 4.4 - Prob. 12ESCh. 4.4 - In Exercises 1 –22, graph each inequality. Ch. 4.4 - Prob. 14ESCh. 4.4 - Prob. 15ESCh. 4.4 - Prob. 16ESCh. 4.4 - In Exercises 1 22, graph each inequality. x2Ch. 4.4 - Prob. 18ESCh. 4.4 - Prob. 19ESCh. 4.4 - Prob. 20ESCh. 4.4 - In Exercises 1 – 22, graph each inequality. Ch. 4.4 - Prob. 22ESCh. 4.4 - In Exercises 23 – 46, graph the solution set of...Ch. 4.4 - Prob. 24ESCh. 4.4 - In Exercises 23 – 46, graph the solution set of...Ch. 4.4 - Prob. 26ESCh. 4.4 - Prob. 27ESCh. 4.4 - Prob. 28ESCh. 4.4 - In Exercises 23 – 46, graph the solution set each...Ch. 4.4 - Prob. 30ESCh. 4.4 - Prob. 31ESCh. 4.4 - Prob. 32ESCh. 4.4 - In Exercises 23 – 46, graph the solution set of...Ch. 4.4 - Prob. 34ESCh. 4.4 - In Exercises 23–46, graph the solution set of each...Ch. 4.4 - Prob. 36ESCh. 4.4 - In Exercises 23 46, graph the solution the...Ch. 4.4 - Prob. 38ESCh. 4.4 - Prob. 39ESCh. 4.4 - Prob. 40ESCh. 4.4 - In Exercises 23–46, graph the solution set of each...Ch. 4.4 - Prob. 42ESCh. 4.4 - Prob. 43ESCh. 4.4 - Prob. 44ESCh. 4.4 - In Exercises 23 46, graph the solution set of...Ch. 4.4 - Prob. 46ESCh. 4.4 - Prob. 47ESCh. 4.4 - Prob. 48ESCh. 4.4 - Prob. 49ESCh. 4.4 - In Exercises 49 – 50, write the given sentences as...Ch. 4.4 - Prob. 51ESCh. 4.4 - Prob. 52ESCh. 4.4 - Prob. 53ESCh. 4.4 - Prob. 54ESCh. 4.4 - Prob. 55ESCh. 4.4 - Prob. 56ESCh. 4.4 - Prob. 57ESCh. 4.4 - Prob. 58ESCh. 4.4 - Prob. 59ESCh. 4.4 - Prob. 60ESCh. 4.4 - Prob. 61ESCh. 4.4 - Prob. 62ESCh. 4.4 - 63. On your next vacation, you will divide lodging...Ch. 4.4 - Prob. 64ESCh. 4.4 - Prob. 65ESCh. 4.4 - Prob. 66ESCh. 4.4 - Prob. 67ESCh. 4.4 - Prob. 68ESCh. 4.4 - Prob. 69ESCh. 4.4 - Prob. 70ESCh. 4.4 - Prob. 71ESCh. 4.4 - Prob. 72ESCh. 4.4 - Prob. 73ESCh. 4.4 - Prob. 74ESCh. 4.4 - Prob. 75ESCh. 4.4 - Prob. 76ESCh. 4.4 - Prob. 77ESCh. 4.4 - Prob. 78ESCh. 4.4 - Prob. 79ESCh. 4.4 - Prob. 80ESCh. 4.4 - Prob. 81ESCh. 4.4 - Prob. 82ESCh. 4.4 - Prob. 83ESCh. 4.4 - Prob. 84ESCh. 4.4 - Prob. 85ESCh. 4.4 - Prob. 86ESCh. 4.4 - Prob. 87ESCh. 4.4 - Prob. 88ESCh. 4.4 - Prob. 89ESCh. 4.4 - Prob. 90ESCh. 4.4 - Prob. 91ESCh. 4.4 - Prob. 92ESCh. 4.4 - Prob. 93ESCh. 4.4 - Prob. 94ESCh. 4.4 - Prob. 95ESCh. 4.4 - Prob. 96ESCh. 4.4 - Prob. 97ESCh. 4.4 - Prob. 98ESCh. 4.4 - a. Graph the solution set of the system:...Ch. 4.4 - Prob. 100ESCh. 4.4 - Prob. 101ESCh. 4.5 - Prob. 1CPCh. 4.5 - Prob. 2CPCh. 4.5 - Prob. 3CPCh. 4.5 - Prob. 4CPCh. 4.5 - Prob. 5CPCh. 4.5 - Fill in each blank so that the resulting statement...Ch. 4.5 - Prob. 2CAVCCh. 4.5 - Prob. 3CAVCCh. 4.5 - Prob. 1ESCh. 4.5 - Prob. 2ESCh. 4.5 - Prob. 3ESCh. 4.5 - Prob. 4ESCh. 4.5 - Prob. 5ESCh. 4.5 - Prob. 6ESCh. 4.5 - Prob. 7ESCh. 4.5 - Prob. 8ESCh. 4.5 - Prob. 9ESCh. 4.5 - Prob. 10ESCh. 4.5 - In Exercises 5 14, an objective function and a...Ch. 4.5 - Prob. 12ESCh. 4.5 - Prob. 13ESCh. 4.5 - Prob. 14ESCh. 4.5 - A television manufacture makes rear – projection...Ch. 4.5 - Prob. 16ESCh. 4.5 - Prob. 17ESCh. 4.5 - Prob. 18ESCh. 4.5 - Prob. 19ESCh. 4.5 - Use the two steps for solving a linear programming...Ch. 4.5 - Use the two steps for solving a linear programming...Ch. 4.5 - Prob. 22ESCh. 4.5 - Prob. 23ESCh. 4.5 - Explaining the Concepts What kinds of problems are...Ch. 4.5 - Prob. 25ESCh. 4.5 - Prob. 26ESCh. 4.5 - Prob. 27ESCh. 4.5 - Prob. 28ESCh. 4.5 - Prob. 29ESCh. 4.5 - Prob. 30ESCh. 4.5 - Make Sense? In Exercises 29 – 32, determine...Ch. 4.5 - Make Sense? In Exercises 29 – 32, determine...Ch. 4.5 - Prob. 33ESCh. 4.5 - Prob. 34ESCh. 4.5 - Prob. 35ESCh. 4.5 - Prob. 36ESCh. 4.5 - Prob. 37ESCh. 4.5 - Prob. 38ESCh. 4.5 - Prob. 39ESCh. 4.5 - Prob. 40ESCh. 4 - In Exercises 1 6, solve each linear inequality....Ch. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 - Prob. 9RECh. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 - Prob. 14RECh. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Prob. 33RECh. 4 - Prob. 34RECh. 4 - Prob. 35RECh. 4 - Prob. 36RECh. 4 - Prob. 37RECh. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - Prob. 43RECh. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 1TCh. 4 - Prob. 2TCh. 4 - Prob. 3TCh. 4 - Prob. 4TCh. 4 - Prob. 5TCh. 4 - Prob. 6TCh. 4 - Prob. 7TCh. 4 - Prob. 8TCh. 4 - Prob. 9TCh. 4 - Prob. 10TCh. 4 - Prob. 11TCh. 4 - Prob. 12TCh. 4 - Prob. 13TCh. 4 - Prob. 14TCh. 4 - Prob. 15TCh. 4 - Prob. 16TCh. 4 - Prob. 17TCh. 4 - Prob. 18TCh. 4 - Prob. 19TCh. 4 - Prob. 20TCh. 4 - Prob. 21TCh. 4 - Prob. 22TCh. 4 - Prob. 23TCh. 4 - In Exercises 1 – 2, solve each equation. Ch. 4 - In Exercises 1 2, solve each equation....Ch. 4 - In Exercises 1 – 2, solve each equation. 3....Ch. 4 - In Exercises 1 2, solve each equation. If...Ch. 4 - In Exercises 1 2, solve each equation. If...Ch. 4 - In Exercises 1 – 2, solve each equation. 6. Use...Ch. 4 - In Exercises 7 – 10, graph each equation or...Ch. 4 - In Exercises 7 10, graph each equation or...Ch. 4 - In Exercises 7 – 10, solve each equation or...Ch. 4 - In Exercises 7 – 10, graph each equation or...Ch. 4 - Prob. 11CRECh. 4 - Prob. 12CRECh. 4 - Prob. 13CRECh. 4 - Prob. 14CRECh. 4 - Which of the following are functions?Ch. 4 - In Exercises 16 20, solve and graph the solution...Ch. 4 - In Exercises 16–20, solve and graph the solution...Ch. 4 - In Exercises 16–20, solve and graph the solution...Ch. 4 - In Exercises 1620,solve and graph the solution set...Ch. 4 - In Exercises 1620, solve and graph the solution...
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
SEE MORE TEXTBOOKS
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY