Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 41, Problem 5A
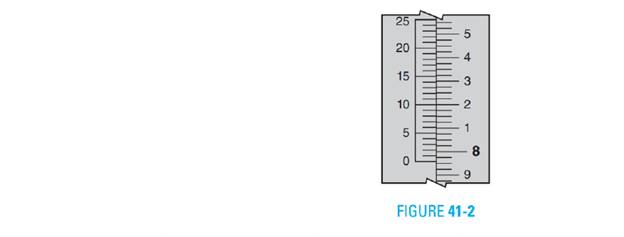
Read the decimal-inch measurement on the vernier height gage in Figure 41-2.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
1
S
0
sin(lnx)
x² - 1
Inx
dx
2
6. Modelling. Suppose that we have two tanks (A and B) between which a mixture of brine
flows. Tank A contains 200 liters of water in which 50 kilograms of salt has been dissolved
and Tank B contains 100 liters of pure water. Water containing 1kg of salt per liter is
pumped into Tank A at the rate of 5 liters per minute. Brine mixture is pumped into
Tank A from Tank B at the rate of 3 liters per minute and brine mixture is pumped from
Tank A into Tank B at the rate of 8 liters per minute. Brine is drained from Tank B at a
rate of 5 liters per minute.
(a) Draw and carefully label a picture of the situation, including both tanks and the flow
of brine between them.
JankA
1ks of
Salt
Slits
Pump
EL
Brine mit
tark A from tank 13
Tank 13
k
3L
zooliters of
Ico liters of
water with
pure water.
Saky salt
→
777
disslore inside
Brine mix is pumped from
tank A to B of 82
Brine drainen
min
by Gf salt (b) Assume all brine mixtures are well-stirred. If we let t be the time in minutes, let x(t)
1ks…
No chatgpt pls
Chapter 41 Solutions
Mathematics For Machine Technology
Ch. 41 - Prob. 1ACh. 41 - Prob. 2ACh. 41 - Use the Table of Block Thicknesses for a Customary...Ch. 41 - Read the setting of the metric vernier micrometer...Ch. 41 - Read the decimal-inch measurement on the vernier...Ch. 41 - Prob. 6ACh. 41 - Add the terms in the following expressions. 18y+yCh. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....
Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions. 4c3+0Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions. 5p+2p2Ch. 41 - Add the terms in the following expressions. a3+2a2Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - Add the terms in the following expressions....Ch. 41 - The machined plate distances shown in Figure 41-3...Ch. 41 - Add the following expressions. 5x+7xy8y9x12xy+13yCh. 41 - Add the following expressions. 3a11d8ma+11d3mCh. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Add the following expressions....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated. 3xyxyCh. 41 - Subtract the following terms as indicated. 3xyxyCh. 41 - Subtract the following terms as indicated. 3xy(xy)Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Prob. 54ACh. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated. 13a9a2Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated. ax2ax2Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated. 213xCh. 41 - Subtract the following terms as indicated. 3x21Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following terms as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Subtract the following expressions as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated. (x)(x2)Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following terms as indicated....Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...Ch. 41 - Multiply the following expressions as indicated...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Remix 4. Direction Fields/Phase Portraits. Use the given direction fields to plot solution curves to each of the given initial value problems. (a) x = x+2y 1111 y = -3x+y with x(0) = 1, y(0) = -1 (b) Consider the initial value problem corresponding to the given phase portrait. x = y y' = 3x + 2y Draw two "straight line solutions" passing through (0,0) (c) Make guesses for the equations of the straight line solutions: y = ax.arrow_forwardIt was homeworkarrow_forwardNo chatgpt pls will upvotearrow_forward
- 18) Find all the complex cube roots of -2i. Leave your answers in polar form with the argument in degrees.arrow_forward9) Write an equation for the hyperbola. 2+ -6-5-4-3-2 -2- -4- -5+ + 23 45 6xarrow_forward8) Find an equation for the hyperbola with vertices at vertices at (±7, 0) and foci at (±9, 0).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL 
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Use of ALGEBRA in REAL LIFE; Author: Fast and Easy Maths !;https://www.youtube.com/watch?v=9_PbWFpvkDc;License: Standard YouTube License, CC-BY
Compound Interest Formula Explained, Investment, Monthly & Continuously, Word Problems, Algebra; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=P182Abv3fOk;License: Standard YouTube License, CC-BY
Applications of Algebra (Digit, Age, Work, Clock, Mixture and Rate Problems); Author: EngineerProf PH;https://www.youtube.com/watch?v=Y8aJ_wYCS2g;License: Standard YouTube License, CC-BY