EBK TRIGONOMETRY
11th Edition
ISBN: 8220102020177
Author: DANIELS
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4.1, Problem 47E
Average Annual Temperature Scientists believe that the average annual temperature in a given location is periodic. The average temperature at a given place during a given season fluctuates as time goes on, from colder to warmer, and back to colder. The graph shows an idealized description of the temperature (in °F) for approximately the last 150 thousand years of a particular location.
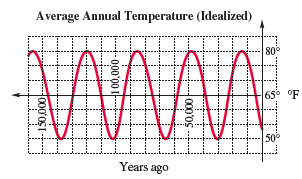
(a) Find the highest and lowest temperatures recorded.
(b) Use these two numbers to find the amplitude.
(c) Find the period of the
(d) What is the trend of the temperature now?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
d₁ ≥ ≥ dn ≥ 0 with di even.
di≤k(k − 1) + + min{k, di}
vi=k+1
T2.5: Let d1, d2,...,d be integers such that n - 1
Prove the equivalence of the Erdos-Gallai conditions:
for each k = 1, 2, ………, n and the Edge-Count Criterion: Σier di + Σjeл(n − 1 − d;) ≥ |I||J| for
all I, JC [n] with In J = 0.
T2.4: Let d₁
T2.3: Prove that there exists a connected graph with degrees d₁ ≥ d₂ >> dn if and only
if d1, d2,..., dn is graphic, d ≥ 1 and di≥2n2. That is, some graph having degree
sequence with these conditions is connected.
Hint - Do not attempt to directly prove this using Erdos-Gallai conditions. Instead work with a
realization and show that 2-switches can be used to make a connected graph with the same degree
sequence. Facts that can be useful: a component (i.e., connected) with n₁ vertices and at least
n₁ edges has a cycle. Note also that a 2-switch using edges from different components of a forest
will not necessarily reduce the number of components. Make sure that you justify that your proof
has a 2-switch that does decrease the number of components.
Chapter 4 Solutions
EBK TRIGONOMETRY
Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 -
CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 -
5. The least positive number x for which cos x =...Ch. 4.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 -
Concept Check Match each function with its graph...Ch. 4.1 - Concept Check Match each function with its graph...
Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 - Concept Check Match each function with its graph...Ch. 4.1 -
Graph each function over the interval [ –2π, 2π]....Ch. 4.1 - Graph each function over the interval [ 2, 2]....Ch. 4.1 - Graph each function over the interval [2, 2]. Give...Ch. 4.1 -
Graph each function over the interval [–2π, 2π]....Ch. 4.1 - Graph each function over the interval [2,2]. Give...Ch. 4.1 -
Graph each function over the interval [–2π,2π]....Ch. 4.1 -
Graph each function over the interval [–2 π,2π]....Ch. 4.1 - Graph each function over the interval [–2π,2π]....Ch. 4.1 - Graph each function over the interval [2,2 ]. Give...Ch. 4.1 - Prob. 22ECh. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 -
Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Graph each function over a two-period interval....Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Connecting Graphs with Equations Determine an...Ch. 4.1 - Average Annual Temperature Scientists believe that...Ch. 4.1 - Blood Pressure Variation The graph gives the...Ch. 4.1 - Prob. 49ECh. 4.1 - Prob. 50ECh. 4.1 - Prob. 51ECh. 4.1 - Prob. 52ECh. 4.1 - Prob. 53ECh. 4.1 - Activity of a Nocturnal Animal Many activities of...Ch. 4.1 -
55. Atmospheric Carbon Dioxide At Mauna Loa....Ch. 4.1 - Atmospheric Carbon Dioxide Refer to Exercise 55....Ch. 4.1 -
57. Average Daily Temperature The temperature in...Ch. 4.1 - 58. Fluctuation in the Solar Constant The solar...Ch. 4.1 -
Musical Sound Waves Pure sounds produce single...Ch. 4.1 - Musical Sound Waves Pure sounds produce single...Ch. 4.1 - Prob. 61ECh. 4.1 - Prob. 62ECh. 4.1 - Prob. 63ECh. 4.1 - Prob. 64ECh. 4.1 - Prob. 65ECh. 4.1 - Prob. 66ECh. 4.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 4.2 -
CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 -
CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.2 - CONCEPT PREVIEW Fill in the blanks to correctly...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function w ith its graph...Ch. 4.2 - Concept Check Match each function w ith its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - Concept Check Match each function with its graph...Ch. 4.2 - The graphs of y = sin x + 1 and y = sin(x + 1) are...Ch. 4.2 - Concept Check Refer to Exercise 17. Which one of...Ch. 4.2 -
Concept Check Match each function in Column I...Ch. 4.2 - Concept Check Match each function in Column I with...Ch. 4.2 -
Concept Check Match each function in Column I...Ch. 4.2 - Concept Check Match each function in Column I with...Ch. 4.2 - Concept Check Fill in each blank with the word...Ch. 4.2 - Prob. 24ECh. 4.2 - Connecting Graphs with equations Each function...Ch. 4.2 - Connecting Graphs with Equations Each function...Ch. 4.2 -
Connecting Graphs with Equations Each function...Ch. 4.2 - Prob. 28ECh. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 - Find the amplitude, the period, any vertical...Ch. 4.2 -
Find the amplitude, the period, any vertical...Ch. 4.2 - Find the amplitude, the period, any vertical...Ch. 4.2 - Find the amplitude, the period, any vertical...Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a two-period interval....Ch. 4.2 -
Graph each function over a two-period interval....Ch. 4.2 - Graph each function over a one-period interval....Ch. 4.2 -
Graph each function over a one-period interval....Ch. 4.2 - Prob. 60ECh. 4.2 - Average Monthly Temperature The average monthly...Ch. 4.2 - Prob. 62ECh. 4.2 - Prob. 63ECh. 4.2 - Prob. 64ECh. 4.2 - Prob. 65ECh. 4.2 - Prob. 66ECh. 4.2 - Prob. 1QCh. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Prob. 3QCh. 4.2 - Prob. 4QCh. 4.2 - Prob. 5QCh. 4.2 - Graph each function over a two-period interval....Ch. 4.2 - Prob. 7QCh. 4.2 - Prob. 8QCh. 4.2 - Prob. 9QCh. 4.2 - Prob. 10QCh. 4.2 - Prob. 11QCh. 4.2 - Prob. 12QCh. 4.3 - 1. The least positive value x for which tan x = 0...Ch. 4.3 - The least positive value x for which cot x = 0 is...Ch. 4.3 - Concept Check Fill in each blank with the word...Ch. 4.3 - Concept Check Fill in each blank with the word...Ch. 4.3 - The negative value k with the greatest value for...Ch. 4.3 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 -
Concept Check Match each function with its...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 - Concept CheckMatch each function with its graph...Ch. 4.3 - Concept Check Match each function with its graph...Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 -
Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 -
Graph each function over a one-period...Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a one-period interval....Ch. 4.3 -
Graph each function over a one-period interval....Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 -
Graph each function over a two-period interval....Ch. 4.3 -
Graph each function over a two-period...Ch. 4.3 -
Graph each function over a two-period...Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 31ECh. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 34ECh. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 36ECh. 4.3 - Graph each function over a two-period interval....Ch. 4.3 - Prob. 38ECh. 4.3 - Prob. 39ECh. 4.3 - Prob. 40ECh. 4.3 - Prob. 41ECh. 4.3 - Prob. 42ECh. 4.3 - Prob. 43ECh. 4.3 - Prob. 44ECh. 4.3 - Concept Check Decide whether each statement is...Ch. 4.3 - Concept CheckDecide whether each statement is true...Ch. 4.3 -
Concept Check Decide whether each statement is...Ch. 4.3 - Prob. 48ECh. 4.3 - Concept Check If c is any number, then how many...Ch. 4.3 - Prob. 50ECh. 4.3 - 51. Show that tan(–x) = –tan x by writing tan(–x)...Ch. 4.3 - 52. Show that cot (–x) = –cot x by writing cot...Ch. 4.3 - Prob. 53ECh. 4.3 - Prob. 54ECh. 4.3 - Prob. 55ECh. 4.3 - Prob. 56ECh. 4.3 - Prob. 57ECh. 4.3 - Prob. 58ECh. 4.3 - Prob. 59ECh. 4.3 - Prob. 60ECh. 4.3 - Prob. 61ECh. 4.3 - Prob. 62ECh. 4.4 - CONCEPT PREVIEW Match each description in Column I...Ch. 4.4 -
CONCEPT PREVIEW Match each description in...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 -
CONCEPT PREVIEW Match each description in Column...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Concept Check Match each function with its graph...Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 -
Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Graph each function over a one-period interval....Ch. 4.4 - Connecting Graphs with EquationsDetermine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Connecting Graphs with Equations Determine an...Ch. 4.4 - Prob. 30ECh. 4.4 - Concept CheckDecide whether each statement is true...Ch. 4.4 - Concept Check Decide whether each statement is...Ch. 4.4 - Concept CheckDecide whether each statement is true...Ch. 4.4 - Prob. 34ECh. 4.4 - 35. Concept Check If c is any number such that -1...Ch. 4.4 - Prob. 36ECh. 4.4 - 37. Show that sec (–x) = sec x by writing sec (–x)...Ch. 4.4 - Prob. 38ECh. 4.4 - Prob. 39ECh. 4.4 - (Modeling) Distance of a Rotating Beacon The...Ch. 4.4 - Prob. 41ECh. 4.4 - Prob. 42ECh. 4.4 - Prob. 43ECh. 4.4 - Prob. 44ECh. 4.4 - Prob. 45ECh. 4.4 - Prob. 46ECh. 4.4 - Prob. 1SECh. 4.4 - Prob. 2SECh. 4.4 - These summary exercises provide practice with the...Ch. 4.4 - Prob. 4SECh. 4.4 - Prob. 5SECh. 4.4 - Prob. 6SECh. 4.4 - Prob. 7SECh. 4.4 -
Graph each function over a two-period...Ch. 4.4 - Prob. 9SECh. 4.4 - Graph each function over a two-period...Ch. 4.5 - CONCEPT PREVIEW Refer to the equations in the...Ch. 4.5 - Prob. 2ECh. 4.5 - CONCEPT PREVIEW Refer to the equations in the...Ch. 4.5 - Prob. 4ECh. 4.5 - Prob. 5ECh. 4.5 - Prob. 6ECh. 4.5 - Spring Motion An object is attached to a coiled...Ch. 4.5 - Spring Motion Repeat Exercise 7, but assume that...Ch. 4.5 - 9. Voltage of an Electrical Circuit The voltage E...Ch. 4.5 - Prob. 10ECh. 4.5 - Particle Movement Write the equation and then...Ch. 4.5 - Prob. 12ECh. 4.5 -
13. Pendulum Motion What are the period P and...Ch. 4.5 - Prob. 14ECh. 4.5 - Spring Motion The formula for the up and down...Ch. 4.5 - Spring Motion (See Exercise 15.) A spring with...Ch. 4.5 - Spring Motion The position of a weight attached to...Ch. 4.5 - Spring Motion The position of a weight attached to...Ch. 4.5 - Spring Motion A weight attached to a spring is...Ch. 4.5 -
20. Spring Motion A weight attached to a spring...Ch. 4.5 -
(Modeling) Springs A weight on a spring has...Ch. 4.5 - Prob. 22ECh. 4.5 -
(Modeling) Springs A weight on a spring has...Ch. 4.5 -
(Modeling) Springs A weight on a spring has...Ch. 4.5 - Prob. 25ECh. 4.5 - Prob. 26ECh. 4.5 - Prob. 27ECh. 4.5 - Prob. 28ECh. 4.5 -
(Modeling) Spring Motion Consider the spring in...Ch. 4.5 - Prob. 30ECh. 4.5 - Prob. 31ECh. 4.5 - (Modeling) Spring Motion Consider the spring in...Ch. 4.5 - Prob. 33ECh. 4.5 - Prob. 34ECh. 4 - Concept Check Which one of the following...Ch. 4 - Prob. 2RECh. 4 - Prob. 3RECh. 4 - Prob. 4RECh. 4 - Prob. 5RECh. 4 - Prob. 6RECh. 4 - Prob. 7RECh. 4 - Prob. 8RECh. 4 -
For each function, give the amplitude, period,...Ch. 4 - Prob. 10RECh. 4 - Prob. 11RECh. 4 - Prob. 12RECh. 4 - Prob. 13RECh. 4 -
For each function, give the amplitude, period,...Ch. 4 - Prob. 15RECh. 4 - Prob. 16RECh. 4 - Prob. 17RECh. 4 - Prob. 18RECh. 4 - Prob. 19RECh. 4 - Prob. 20RECh. 4 - Prob. 21RECh. 4 - Prob. 22RECh. 4 - Prob. 23RECh. 4 - Prob. 24RECh. 4 - Prob. 25RECh. 4 - Prob. 26RECh. 4 - Prob. 27RECh. 4 - Prob. 28RECh. 4 - Prob. 29RECh. 4 - Prob. 30RECh. 4 - Prob. 31RECh. 4 - Prob. 32RECh. 4 - Graph each function over a one-period...Ch. 4 -
Graph each function over a one-period...Ch. 4 -
Graph each function over a one-period...Ch. 4 - Prob. 36RECh. 4 -
Graph each function over a one-period...Ch. 4 - Prob. 38RECh. 4 - Prob. 39RECh. 4 - Prob. 40RECh. 4 - Prob. 41RECh. 4 - Prob. 42RECh. 4 - (Modeling) Monthly Temperatures A set of...Ch. 4 - Prob. 44RECh. 4 - Prob. 45RECh. 4 - Prob. 46RECh. 4 - Prob. 47RECh. 4 - Prob. 48RECh. 4 - Prob. 49RECh. 4 - Prob. 50RECh. 4 - Prob. 51RECh. 4 - Prob. 52RECh. 4 - Prob. 53RECh. 4 - Prob. 54RECh. 4 - Prob. 55RECh. 4 - Prob. 56RECh. 4 - Prob. 57RECh. 4 - Prob. 58RECh. 4 - Prob. 1TCh. 4 - Prob. 2TCh. 4 - Prob. 3TCh. 4 - Prob. 4TCh. 4 - Prob. 5TCh. 4 - Prob. 6TCh. 4 - Prob. 7TCh. 4 - Prob. 8TCh. 4 - Prob. 9TCh. 4 - Prob. 10TCh. 4 - Prob. 11TCh. 4 - Prob. 12TCh. 4 - Average Monthly Temperature The average monthly...Ch. 4 -
14. Spring Motion The position of a weight...Ch. 4 - Prob. 15T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Similar questions
- T2.2 Prove that a sequence s d₁, d₂,..., dn with n ≥ 3 of integers with 1≤d; ≤ n − 1 is the degree sequence of a connected unicyclic graph (i.e., with exactly one cycle) of order n if and only if at most n-3 terms of s are 1 and Σ di = 2n. (i) Prove it by induction along the lines of the inductive proof for trees. There will be a special case to handle when no d₂ = 1. (ii) Prove it by making use of the caterpillar construction. You may use the fact that adding an edge between 2 non-adjacent vertices of a tree creates a unicylic graph.arrow_forward= == T2.1: Prove that the necessary conditions for a degree sequence of a tree are sufficient by showing that if di 2n-2 there is a caterpillar with these degrees. Start the construction as follows: if d1, d2,...,d2 and d++1 = d = 1 construct a path v1, v2, ..., vt and add d; - 2 pendent edges to v, for j = 2,3,..., t₁, d₁ - 1 to v₁ and d₁ - 1 to v₁. Show that this construction results vj in a caterpillar with degrees d1, d2, ..., dnarrow_forward4 sin 15° cos 15° √2 cos 405°arrow_forward
- 2 18-17-16-15-14-13-12-11-10 -9 -8 -6 -5 -4-3-2-1 $ 6 8 9 10 -2+ The curve above is the graph of a sinusoidal function. It goes through the points (-10, -1) and (4, -1). Find a sinusoidal function that matches the given graph. If needed, you can enter π-3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Questionarrow_forwardketch a graph of the function f(x) = 3 cos (표) 6. x +1 5 4 3 3 80 9 2+ 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3+ -4 5 -6+ Clear All Draw: пи > Next Questionarrow_forwardDraw the following graph on the interval πT 5π < x < 2 2 y = 2 sin (2(x+7)) 6. 5. 4 3 3 2 1 +3 /2 -π/3 -π/6 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/311π/6 2π 13π/67π/3 5π Clear All Draw:arrow_forward
- ketch a graph of the function f(x) = 3 cos (표) 6. x +1 5 4 3 3 80 9 2+ 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3+ -4 5 -6+ Clear All Draw: пи > Next Questionarrow_forward3 2 20-10-18-17-16-15-14-13-12-11-10-9 -8 -7 -6 -$4-3-2-1 -1 -2 -3 4- -5+ The curve above is the graph of a sinusoidal function. It goes through the points (-8, -4) and (6,-4). Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Question Barrow_forwardX Grades for X Assignmen X A-Z Datab XE Biocultural X EBSCO-Ful X Review es/119676/assignments/3681238 Review Quiz 8.1-p2 points possible Answered: 3/5 ● Question 1 4+ 3. 2 1 13 /12-11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 -1 -2 -3 -4- 5 2 6 The curve above is the graph of a sinusoidal function. It goes through the points (-7,0) and (3,0). Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Question 申 J % F 刀 Q Search S € t ח Y 7 I * 00 J ப I Darrow_forward
- 2 d) Draw the following graph on the interval k 5π Next Questionarrow_forwardDraw the following graph on the interval 5л Next Questionarrow_forwardDraw the following graph on the interval πT 5π < x < x≤ 2 2 y = 2 cos(3(x-77)) +3 6+ 5 4- 3 2 1 /2 -π/3 -π/6 Clear All Draw: /6 π/3 π/2 2/3 5/6 x 7/6 4/3 3/2 5/311/6 2 13/67/3 5 Question Help: Video Submit Question Jump to Answerarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Sine, Cosine and Tangent graphs explained + how to sketch | Math Hacks; Author: Math Hacks;https://www.youtube.com/watch?v=z9mqGopdUQk;License: Standard YouTube License, CC-BY