
Concept explainers
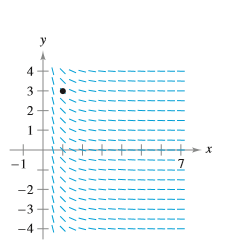
Slope Field In Exercises 45 and 46, a
Want to see the full answer?
Check out a sample textbook solution
Chapter 4 Solutions
Student Solutions Manual for Larson/Edwards' Calculus of a Single Variable, 11th
- Find the maximum and minimum values of the function f(x, y) = e² subject to ï³ + y³ = 128 Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. Maximum value:arrow_forwardA chemical manufacturing plant can produce x units of chemical Z given p units of chemical P and 7 units of chemical R, where: z = 140p0.6,0.4 Chemical P costs $300 a unit and chemical R costs $1,500 a unit. The company wants to produce as many units of chemical Z as possible with a total budget of $187,500. A) How many units each chemical (P and R) should be "purchased" to maximize production of chemical Z subject to the budgetary constraint? Units of chemical P, p = Units of chemical R, r = B) What is the maximum number of units of chemical Z under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production, z= unitsarrow_forwardA firm manufactures a commodity at two different factories, Factory X and Factory Y. The total cost (in dollars) of manufacturing depends on the quantities, and y produced at each factory, respectively, and is expressed by the joint cost function: C(x, y) = x² + xy +4y²+400 A) If the company's objective is to produce 1,900 units per month while minimizing the total monthly cost of production, how many units should be produced at each factory? (Round your answer to whole units, i.e. no decimal places.) To minimize costs, the company should produce: units at Factory X and units at Factory Y B) For this combination of units, their minimal costs will be enter any commas in your answer.) Question Help: Video dollars. (Do notarrow_forward
- use Lagrange multipliers to solvearrow_forwardSuppose a Cobb-Douglas Production function is given by the following: P(L,K)=80L0.75 K-0.25 where L is units of labor, K is units of capital, and P(L, K) is total units that can be produced with this labor/capital combination. Suppose each unit of labor costs $400 and each unit of capital costs $1,600. Further suppose a total of $384,000 is available to be invested in labor and capital (combined). A) How many units of labor and capital should be "purchased" to maximize production subject to your budgetary constraint? Units of labor, L = Units of capital, K = B) What is the maximum number of units of production under the given budgetary conditions? (Round your answer to the nearest whole unit.) Max production = unitsarrow_forwardSuppose a Cobb-Douglas Production function is given by the function: P(L, K) = 7L0.0 K0.4 Furthemore, the cost function for a facility is given by the function: C(L, K) = 100L +400K Suppose the monthly production goal of this facility is to produce 15,000 items. In this problem, we will assume L represents units of labor invested and K represents units of capital invested, and that you can invest in tenths of units for each of these. What allocation of labor and capital will minimize total production Costs? Units of Labor L = Units of Capital K = (Show your answer is exactly 1 decimal place) (Show your answer is exactly 1 decimal place) Also, what is the minimal cost to produce 15,000 units? (Use your rounded values for L and K from above to answer this question.) The minimal cost to produce 15,000 units is $ Hint: 1. Your constraint equation involves the Cobb Douglas Production function, not the Cost function. 2. When finding a relationship between L and K in your system of equations,…arrow_forward
- Find the absolute maximum and minimum of f(x, y) = x + y within the domain x² + y² ≤ 4. Please show your answers to at least 4 decimal places. Enter DNE if the value does not exist. 1. Absolute minimum of f(x, y) isarrow_forwardSuppose that one factory inputs its goods from two different plants, A and B, with different costs, 3 and 7 each respective. And suppose the price function in the market is decided as p(x, y) = 100 - x - y where I and y are the demand functions and 0 < x,y. Then as x = y = the factory can attain the maximum profit,arrow_forwardEvaluate the following integrals, showing all your workingarrow_forward
- Consider the function f(x) = 2x³-4x2-x+1. (a) Without doing a sketch, show that the cubic equation has at least one solution on the interval [0,1]. Use a theorem discussed in lectures, or see Section 1.8 of Calculus (7th ed) by Stewart. Ensure that the conditions of the theorem are satisfied (include this in your solution) (b) Now, by sketching the cubic (by hand or by computer), you should see that there is, in fact, exactly one zero in the interval [0,1]. Use Newton's method to find this zero accurate to 3 decimal places. You should include a sketch of the cubic, Newton's iteration formula, and the list of iterates. [Use a computer if possible, e.g., a spreadsheet or MatLab.]arrow_forwardEvaluate the following integrals, showing all your workingarrow_forwardDifferentiate the following functionarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning


