Concept explainers
Videos
a.
Construct box plot of the variable price.
Identify whether there are outliers or not.
Find the
Find the first
Find the third quartile value.
a.
Answer to Problem 37CE
Output of box plot for the variable price using MINITAB software is,
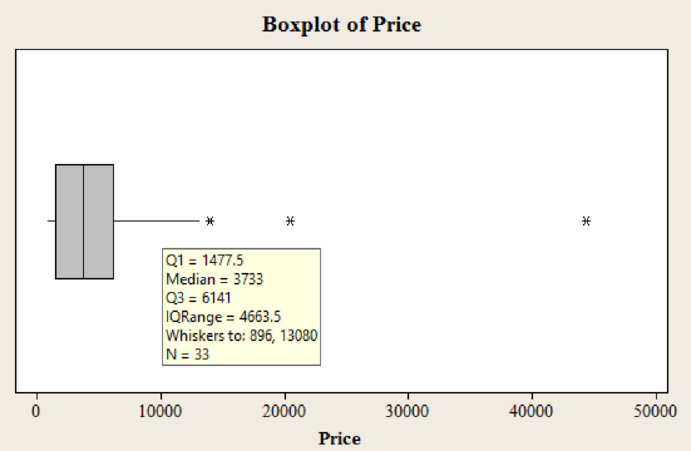
Yes, there are 3 outliers in the dataset.
The median price is 3,733.
The first quartile value is 1,478.
The third quartile value is 6,141.
Explanation of Solution
Calculation:
Step by step procedure to obtain boxplot using MINITAB software is given as,
- Choose Graph > Boxplot.
- In Graph variables enter the columns Price.
- Click OK.
Outliers:
In the boxplot, the outlier is represented using asterisk. In the boxplot of data set there are 3 asterisks representing outliers. Hence, there are three outliers in the dataset.
Median:
The median is the middle value of the data set. In the boxplot, the line in middle of the box represents median of the dataset. The line corresponds to value 3,733.
Hence, the median value is 3,733.
First quartile:
The border line towards the left side of the box represents the value of first quartile. In this box plot, the line of the box on left side corresponds to the value approximately 1,478.
Hence, the third quartile value is 6,141.
Third quartile:
The border line towards the right side of the box represents the value of third quartile. In this box plot, the line of the box on right side corresponds to the value approximately 6,141.
Hence, the first quartile value is 1,478.
b.
Construct box plot of the variable size.
Identify whether there are outliers or not.
Find the median price.
Find the first quartile value.
Find the third quartile value.
b.
Answer to Problem 37CE
Output of box plot for the variable size using MINITAB software is,
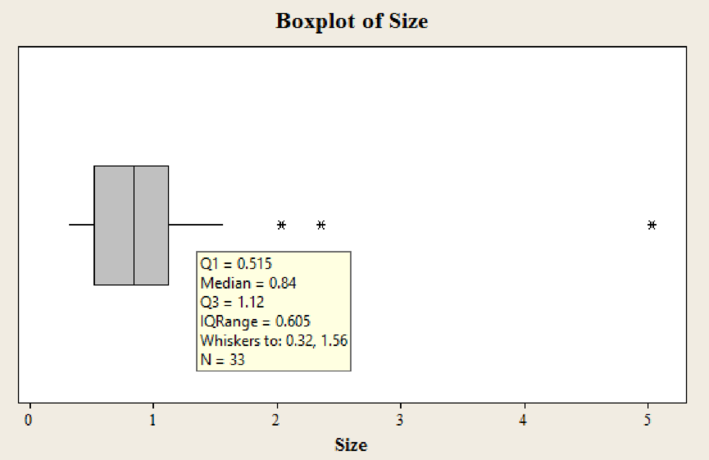
Yes, there are 3 outliers in the dataset.
The median price is 0.84.
The first quartile value is 0.515.
The third quartile value is 1.12.
Explanation of Solution
Calculation:
Step by step procedure to obtain boxplot using MINITAB software is given as,
- Choose Graph > Boxplot.
- In Graph variables enter the columns Size.
- Click OK.
Outliers:
In the boxplot, the outlier is represented using asterisk. In the boxplot of data set there are 3 asterisks representing outliers. Hence, there are three outliers in the dataset.
Median:
The median is the middle value of the data set. In the boxplot, the line in middle of the box represents median of the dataset. The line corresponds to value 0.84.
Hence, the median value is 0.84.
First quartile:
The border line towards the left side of the box represents the value of first quartile. In this box plot, the line of the box on left side corresponds to the value approximately 0.515.
Hence, the third quartile value is 0.515.
Third quartile:
The border line towards the right side of the box represents the value of third quartile. In this box plot, the line of the box on right side corresponds to the value approximately 1.12.
Hence, the first quartile value is 1.12.
c.
Construct
Identify whether there is association between the two variables or not.
Identify whether association is direct or indirect.
Identify whether any point seems to be different from the others.
c.
Answer to Problem 37CE
Output of scatter diagram for variables price and size using MINITAB software is,
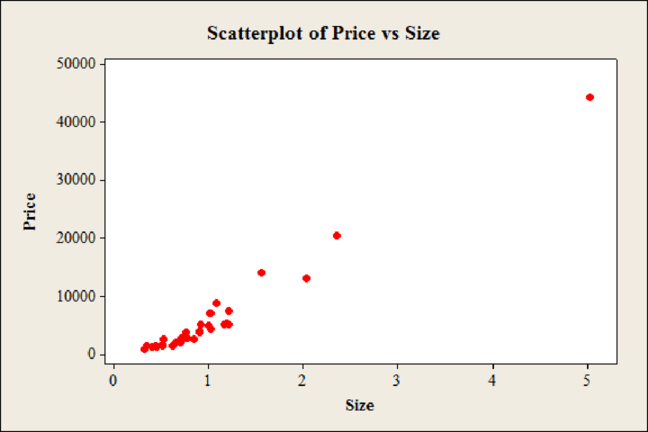
Yes, there is association between the variables price and size.
The association is direct.
Yes, the first observation of both the price and size is large when compared to other observations.
Explanation of Solution
Calculation:
Step by step procedure to obtain scatter diagram using MINITAB software is given as,
- Choose Graph > Scatterplot > select Simple.
- In Y variable enter the column Price.
- In X variable enter the column Size.
- Click OK.
In the scatter diagram it can be observed that, the Price has increased as the Size increases indicating that the association between the variables.
Hence, there is association between the variables price and size
The relation is said to be direct if value of one variable increases due to effect of another variable. From the scatter diagram, the value of Price has increased as the Size increases indicating a direct or positive association.
Hence, the association is direct.
From the scatter diagram, it can be observed that one of the observations corresponding to the value of 5.03 carats for size and $44,312 for price is far from all the other observations. Hence, one point seems to be different from the others.
d.
Construct a
Find the most common cut grade.
Find the most common shape.
Find the most common combination of cut grade and shape.
d.
Answer to Problem 37CE
The contingency table for the variables shape and cut grade is,
| Shape | Cut Grade | |||||
| Average | Good | Ideal | Premium | Ultra Ideal | Total | |
| Emerald | 0 | 0 | 1 | 0 | 0 | 1 |
| Marquise | 0 | 2 | 0 | 1 | 0 | 3 |
| Oval | 0 | 0 | 0 | 1 | 0 | 1 |
| Princess | 1 | 0 | 2 | 2 | 0 | 5 |
| Round | 1 | 3 | 3 | 13 | 3 | 23 |
| Total | 2 | 5 | 6 | 17 | 3 | 33 |
The most common cut grade is premium.
The most common shape is round.
The most common combination of cut grade and shape is premium and round.
Explanation of Solution
Calculation:
Contingency table:
A table that is used for classifying observations based on the two identifiable characteristics is termed as contingency table. It is used for summarizing two variables.
The variable cut grade is classified into 5 different categories ‘average, good, ideal, premium, ultra ideal’. The variable shape is classified into 5 different categories ‘emerald, marquise, oval, princess, and round’.
Count the number of cut grades are average with shape of emerald. From the data, there is no combination of average cut grades with shape of emerald. Hence, the frequency is 0.
Similarly, count the frequency for each of the possible combination of cut grade and shape. Then calculate the totals for each column and row. The contingency table is obtained as below,
| Shape | Cut Grade | |||||
| Average | Good | Ideal | Premium | Ultra Ideal | Total | |
| Emerald | 0 | 0 | 1 | 0 | 0 | 1 |
| Marquise | 0 | 2 | 0 | 1 | 0 | 3 |
| Oval | 0 | 0 | 0 | 1 | 0 | 1 |
| Princess | 1 | 0 | 2 | 2 | 0 | 5 |
| Round | 1 | 3 | 3 | 13 | 3 | 23 |
| Total | 2 | 5 | 6 | 17 | 3 | 33 |
The cut grade ‘Premium’ has a total of 17, which is large when compared to other cut grades. This shows that, the most common cut grade of diamonds is ‘Premium.
Hence, the most common cut grade is premium.
The shape ‘Round’ has a total of 23, which is large when compared to other shapes. This shows that, the most common shape of diamonds is ‘Round’.
Hence, the most common shape is round.
The combination of cut grade ‘Premium’ and shape ‘Round’ has a total of 13, which is large when compared to other combinations. This shows that, the most common combination of diamonds is cut grade ‘Premium’ and shape ‘Round’.
Hence, the most common combination of cut grade and shape is premium and round.
Want to see more full solutions like this?
Chapter 4 Solutions
Statistical Techniques in Business and Economics
- Install RStudio: Begin by installing RStudio on your computer. If you haven't done so, please refer to the official RStudio website for download and installation instructions. Watch the Tutorial Video: Watch the provided video tutorial that explains how to run RStudio. Pay close attention to the steps for opening and managing data files. https://www.youtube.com/watch?v=RhJp6vSZ7z0 Open RStudio: Once RStudio is installed, open the application. Load the Dataset: In RStudio, open a data file named "mtcars". To do this, type the command mtcars in the script editor and run the command. Attach the Data: Next, attach the dataset using the command attach(mtcars). Examine the Variables: Carefully review and note the names of all variables in the dataset. Examples of these variables include: Mileage (mpg) Number of Cylinders (cyl) Displacement (disp) Horsepower (hp) Research: Google to understand these variables. Statistical Analysis: Select mpg variable, and perform the following…arrow_forwardA marketing professor has surveyed the students at her university to better understand attitudes towards PPT usage for higher education. To be able to make inferences to the entire student body, the sample drawn needs to represent the university’s student population on all key characteristics. The table below shows the five key student demographic variables. The professor found the breakdown of the overall student body in the university’s fact book posted online. A non-parametric chi-square test was used to test the sample demographics against the population percentages shown in the table above. Review the output for the five chi-square tests on the following pages and answer the five questions: Based on the chi-square test, which sample variables adequately represent the university’s student population and which ones do not? Support your answer by providing the p-value of the chi-square test and explaining what it means. Using the results from Question 1, make recommendation for…arrow_forwardA marketing professor has surveyed the students at her university to better understand attitudes towards PPT usage for higher education. To be able to make inferences to the entire student body, the sample drawn needs to represent the university’s student population on all key characteristics. The table below shows the five key student demographic variables. The professor found the breakdown of the overall student body in the university’s fact book posted online. A non-parametric chi-square test was used to test the sample demographics against the population percentages shown in the table above. Review the output for the five chi-square tests on the following pages and answer the five questions: Based on the chi-square test, which sample variables adequately represent the university’s student population and which ones do not? Support your answer by providing the p-value of the chi-square test and explaining what it means. Using the results from Question 1, make recommendation for…arrow_forward
- A retail chain is interested in determining whether a digital video point-of-purchase (POP) display would stimulate higher sales for a brand advertised compared to the standard cardboard point-of-purchase display. To test this, a one-shot static group design experiment was conducted over a four-week period in 100 different stores. Fifty stores were randomly assigned to the control treatment (standard display) and the other 50 stores were randomly assigned to the experimental treatment (digital display). Compare the sales of the control group (standard POP) to the experimental group (digital POP). What were the average sales for the standard POP display (control group)? What were the sales for the digital display (experimental group)? What is the (mean) difference in sales between the experimental group and control group? List the null hypothesis being tested. Do you reject or retain the null hypothesis based on the results of the independent t-test? Was the difference between the…arrow_forwardWhat were the average sales for the four weeks prior to the experiment? What were the sales during the four weeks when the stores used the digital display? What is the mean difference in sales between the experimental and regular POP time periods? State the null hypothesis being tested by the paired sample t-test. Do you reject or retain the null hypothesis? At a 95% significance level, was the difference significant? Explain why or why not using the results from the paired sample t-test. Should the manager of the retail chain install new digital displays in each store? Justify your answer.arrow_forwardA retail chain is interested in determining whether a digital video point-of-purchase (POP) display would stimulate higher sales for a brand advertised compared to the standard cardboard point-of-purchase display. To test this, a one-shot static group design experiment was conducted over a four-week period in 100 different stores. Fifty stores were randomly assigned to the control treatment (standard display) and the other 50 stores were randomly assigned to the experimental treatment (digital display). Compare the sales of the control group (standard POP) to the experimental group (digital POP). What were the average sales for the standard POP display (control group)? What were the sales for the digital display (experimental group)? What is the (mean) difference in sales between the experimental group and control group? List the null hypothesis being tested. Do you reject or retain the null hypothesis based on the results of the independent t-test? Was the difference between the…arrow_forward
- Question 4 An article in Quality Progress (May 2011, pp. 42-48) describes the use of factorial experiments to improve a silver powder production process. This product is used in conductive pastes to manufacture a wide variety of products ranging from silicon wafers to elastic membrane switches. Powder density (g/cm²) and surface area (cm/g) are the two critical characteristics of this product. The experiments involved three factors: reaction temperature, ammonium percentage, stirring rate. Each of these factors had two levels, and the design was replicated twice. The design is shown in Table 3. A222222222222233 Stir Rate (RPM) Ammonium (%) Table 3: Silver Powder Experiment from Exercise 13.23 Temperature (°C) Density Surface Area 100 8 14.68 0.40 100 8 15.18 0.43 30 100 8 15.12 0.42 30 100 17.48 0.41 150 7.54 0.69 150 8 6.66 0.67 30 150 8 12.46 0.52 30 150 8 12.62 0.36 100 40 10.95 0.58 100 40 17.68 0.43 30 100 40 12.65 0.57 30 100 40 15.96 0.54 150 40 8.03 0.68 150 40 8.84 0.75 30 150…arrow_forward- + ++ Table 2: Crack Experiment for Exercise 2 A B C D Treatment Combination (1) Replicate I II 7.037 6.376 14.707 15.219 |++++ 1 བྱ॰༤༠སྦྱོ སྦྱོཋཏྟཱུ a b ab 11.635 12.089 17.273 17.815 с ас 10.403 10.151 4.368 4.098 bc abc 9.360 9.253 13.440 12.923 d 8.561 8.951 ad 16.867 17.052 bd 13.876 13.658 abd 19.824 19.639 cd 11.846 12.337 acd 6.125 5.904 bcd 11.190 10.935 abcd 15.653 15.053 Question 3 Continuation of Exercise 2. One of the variables in the experiment described in Exercise 2, heat treatment method (C), is a categorical variable. Assume that the remaining factors are continuous. (a) Write two regression models for predicting crack length, one for each level of the heat treatment method variable. What differences, if any, do you notice in these two equations? (b) Generate appropriate response surface contour plots for the two regression models in part (a). (c) What set of conditions would you recommend for the factors A, B, and D if you use heat treatment method C = +? (d) Repeat…arrow_forwardQuestion 2 A nickel-titanium alloy is used to make components for jet turbine aircraft engines. Cracking is a potentially serious problem in the final part because it can lead to nonrecoverable failure. A test is run at the parts producer to determine the effect of four factors on cracks. The four factors are: pouring temperature (A), titanium content (B), heat treatment method (C), amount of grain refiner used (D). Two replicates of a 24 design are run, and the length of crack (in mm x10-2) induced in a sample coupon subjected to a standard test is measured. The data are shown in Table 2. 1 (a) Estimate the factor effects. Which factor effects appear to be large? (b) Conduct an analysis of variance. Do any of the factors affect cracking? Use a = 0.05. (c) Write down a regression model that can be used to predict crack length as a function of the significant main effects and interactions you have identified in part (b). (d) Analyze the residuals from this experiment. (e) Is there an…arrow_forward
- A 24-1 design has been used to investigate the effect of four factors on the resistivity of a silicon wafer. The data from this experiment are shown in Table 4. Table 4: Resistivity Experiment for Exercise 5 Run A B с D Resistivity 1 23 2 3 4 5 6 7 8 9 10 11 12 I+I+I+I+Oooo 0 0 ||++TI++o000 33.2 4.6 31.2 9.6 40.6 162.4 39.4 158.6 63.4 62.6 58.7 0 0 60.9 3 (a) Estimate the factor effects. Plot the effect estimates on a normal probability scale. (b) Identify a tentative model for this process. Fit the model and test for curvature. (c) Plot the residuals from the model in part (b) versus the predicted resistivity. Is there any indication on this plot of model inadequacy? (d) Construct a normal probability plot of the residuals. Is there any reason to doubt the validity of the normality assumption?arrow_forwardStem1: 1,4 Stem 2: 2,4,8 Stem3: 2,4 Stem4: 0,1,6,8 Stem5: 0,1,2,3,9 Stem 6: 2,2 What’s the Min,Q1, Med,Q3,Max?arrow_forwardAre the t-statistics here greater than 1.96? What do you conclude? colgPA= 1.39+0.412 hsGPA (.33) (0.094) Find the P valuearrow_forward
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL