Chapter 4, Problem 1SE

Mark each statement True or False. Justify each answer. (If true, cite appropriate facts or theorems. If false, explain why or give a counterexample that shows why the statement is not true in every case.) In parts (a)-(f), v₁, ..., v_p are vectors in a nonzero finite-dimensional vector space V, and S = {v₁, ..., v_p}.

1. a. The set of all linear combinations of v₁, ..., v_p is a vector space.
2. b. If {v₁, ..., v_p−1} spans V, then S spans V.
3. c. If {v₁, ..., v_p−1} is linearly independent, then so is S.
4. d. If S is linearly independent, then S is a basis for V.
5. e. If Span S = V, then some subset of S is a basis for V.
6. f. If dim V = p and Span, S = V, then S cannot be linearly dependent.
7. g. A plane in ℝ³ is a two-dimensional subspace.
8. h. The nonpivot columns of a matrix are always linearly dependent.
9. i. Row operations on a matrix A can change the linear dependence relations among the rows of A.
10. j. Row operations on a matrix can change the null space.
11. k. The rank of a matrix equals the number of nonzero rows.
12. l. If an m × n matrix A is row equivalent to an echelon matrix U and if U has k nonzero rows, then the dimension of the solution space of Ax = 0 is m − k.
13. m. If B is obtained from a matrix A by several elementary row operations, then rank B = rank A.
14. n. The nonzero rows of a matrix A form a basis for Row A.
15. ○.      If matrices A and B have the same reduced echelon form, then Row A = Row B.
16. p. If H is a subspace of ℝ³, then there is a 3 × 3 matrix A such that H = Col A.
17. q. If A is m × n and rank A = m, then the linear transformation x ↦ Ax is one-to-one.
18. r. If A is m × n and the linear transformation x ↦ Ax is onto, then rank A = m.
19. s. A change-of-coordinates matrix is always invertible.
20. t. If B = {b₁, ..., b_n} and C = {c₁, ..., c_n} are bases for a vector space V, then the jth column of the change-of-coordinates matrix 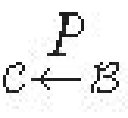is the coordinate vector [c_j]_B.

To determine

To find: Whether the statement “The set of all linear combinations of $v_1,\dots ,v_p$ is a vector space” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

Here, the given vectors are $v_1,\dots ,v_p$.

The span { $v_1,\dots ,v_p$} always form a vector subspace of the vector space.

Thus, the linear combinations of $v_1,\dots ,v_p$ are also a vector space.

Hence, the statement is true.

To determine

To find: Whether the statement “If $\left\{v_1,\dots ,v_{p-1}\right\}$ spans V, then S spans V” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

The set S is $S=\left\{v_1,\dots ,v_p\right\}$.

It is given that the set $\left\{v_1,\dots ,v_{p-1}\right\}$ spans V. That is, span $\left\{v_1,\dots ,v_{p-1}\right\}$= $V$.

That is, every element in the vector space $V$ can be expressed by using the vectors $\left\{v_1,\dots ,v_{p-1}\right\}$.

Here, the set $S=\left\{v_1,\dots ,v_p\right\}$, the set contain more than one element than the set $\left\{v_1,\dots ,v_{p-1}\right\}$.

The smaller set $\left\{v_1,\dots ,v_{p-1}\right\}$ spans V which implies the bigger set $S=\left\{v_1,\dots ,v_p\right\}$ also spans V.

If the vector space V is spanned by $\left\{v_1,\dots ,v_{p-1}\right\}$, then its linear combinations also span V.

Hence, the statement is true.

To determine

To find: Whether the statement “If $\left\{v_1,\dots ,v_{p-1}\right\}$ is linearly independent, then so is S” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

If $\left\{v_1,\dots ,v_{p-1}\right\}$ is a set of linearly independent vectors, then it does not imply that the set $\left\{v_1,\dots ,v_{p-1},v_p\right\}$ is also linearly independent as $v_p$ may be expressed as a linear combination of $\left\{v_1,\dots ,v_{p-1}\right\}$.

Therefore, it does not imply that S is linearly independent.

Hence, the statement is false.

To determine

To find: Whether the statement “If S is linearly independent then S is a basis for V” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

A set of vectors $\left\{v_1,\dots ,v_p\right\}$ is a basis for a vector space V if the following two conditions are satisfied:

1. The set of vectors $\left\{v_1,\dots ,v_p\right\}$ is a linearly independent set.

2. The set $\left\{v_1,\dots ,v_p\right\}$ spans the vector space V.

It can be seen that the second condition is not satisfied.

Hence, the statement is false.

To determine

To find: Whether the statement “If $\text{Span }S=V$, then some subset of S is a basis for V” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

It is given that the vector space V is spanned by S, which is nonzero set.

Suppose the set S is linearly independent then, the set S form a basis for V.

Suppose the set S is linearly dependent then, some subset of S linearly independent and which spans V.

That is, some subset of S form a basis for V.

Hence, the statement is true.

To determine

To find: Whether the statement “If $\dim V=p$ and $\text{Span }S=V$, then S cannot be linearly dependent.” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

It is given that $\dim V=p$. That is, the basis of the vector space contain $p$ elements

Here, $\text{Span }S=V$, that is the set contain $p$ elements span the $p$ dimensional space.

Which implies the $p$ elements is linearly independent.

Hence, the statement is false.

To determine

To find: Whether the statement “A plane in ${ℝ}^3$ is a two-dimensional subspace” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

Every plane in ${ℝ}^3$ to be a two dimensional subspace is false.

Sometimes plane in ${ℝ}^3$ does not form a vector space. Only the plane passing through origin form a subspace of ${ℝ}^3$.

Hence, the statement is false.

To determine

To find: Whether the statement “The non-pivot columns of a matrix are always linearly dependent” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

Consider the matrix $\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]$.

Here non-pivot columns are linearly independent.

Hence, the statement is false.

To determine

To find: Whether the statement “Row operations on a matrix A can change the linear dependence relations among the rows of A” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

Row operations on matrix $A$ change the matrix. Thus, this changes the dependence relation among the rows of a matrix.

Hence, the statement is true.

To determine

To find: Whether the statement “Row operations on a matrix can change the null space” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

Row operations do not change the solution set of the system $Ax=0$.

Therefore, row operations do not change the null space.

Hence, the statement is false.

To determine

To find: Whether the statement “The rank of a matrix equals the number of nonzero rows” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

The rank of a matrix A is the dimension of the column space of A.

The dimension of column space of A is the number of pivot columns in A.

Therefore, the rank of matrix equals the number of pivot columns.

Consider the matrix $\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]$.

The above matrix has 2 rows but rank of the matrix is 1.

Hence, the statement is false.

To determine

To find: Whether the statement “If an $m\times n$ matrix A is row equivalent to an echelon matrix U and if U has k nonzero rows, then the dimension of the solution space of $Ax=0$ is $m-k$” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

If U has k nonzero rows then, $\text{rank }A=k$.

According to the Rank Theorem, the rank of an $m\times n$ matrix A is same as the dimension of the column space of A and is equal to the number of pivot positions in A such that,

$\begin{array}{c}\text{rank }A+\dim \text{Nul }A=n\\ \dim \text{Nul }A=n-\text{rank }A\\ =n-k\end{array}$

Hence, the statement is false.

To determine

To find: Whether the statement “If B is obtained from a matrix A by several elementary row operations, then $\text{rank }A=\text{rank }B$” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

Elementary row operations does not change the number of pivot columns and hence, does not change the rank of a matrix.

Therefore, the rank of matrix B will be same as the rank of matrix A.

Hence, the statement is true.

To determine

To find: Whether the statement “The nonzero rows of a matrix A form a basis for Row A” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

To form a basis for A, the rows have to span A and should also be linearly independent.

The nonzero rows of a matrix A span Row A but that does not guarantee that they are linearly independent.

Hence, the statement is false.

To determine

To find: Whether the statement “If matrices A and B have the same reduced echelon form, then $\text{Row }A=\text{Row }B$” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

The nonzero rows of the echelon form of a matrix, form a basis for the row space of that matrix.

If the echelon form for two matrices is same, then the basis for the row spaces is also same.

Since, row spaces are vector spaces and if two vector spaces have same basis, then the vector spaces are same.

Hence, the statement is true.

To determine

To find: Whether the statement “If H is a subspace of ${ℝ}^3$, then there is a $3\times 3$ matrix A such that $H=\text{Col }A$” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

If H is a zero, 1, 2, or 3 dimensional subspace of ${ℝ}^3$, there will always be a corresponding $3\times 3$ matrix A formed by the basis of H.

The basis of H will then be in the column space of A.

Therefore, $H=\text{Col }A$.

Hence, the statement is true.

To determine

To find: Whether the statement “If A is $m\times n$ and $\text{rank }A=m$, then the linear transformation $x\mapsto Ax$ is one-to-one” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

Here the matrix A is linear transformation from $R^m$ to $R^n$.

The transformation $x\mapsto Ax$ is one-to-one if and only if null space of $A$ is zero.

Here, rank of the matrix is A thus, by the rank nullity theorem null space of $A$ contain $n-m$ elements.

Hence, the statement is false.

To determine

To find: Whether the statement “If A is $m\times n$ and the linear transformation $x\mapsto Ax$ is onto, then $\text{rank }A=m$.)” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

Here the matrix A is linear transformation from $R^m$ to $R^n$.

If the transformation is onto then, $\text{Col }A={ℝ}^m$

The rank of a matrix A is the dimension of the column space of A.

Therefore, the rank of A is m.

Hence, the statement is true.

To determine

To find: Whether the statement “A change-of-coordinate matrix is always invertible” is true or false.

Answer to Problem 1SE

The statement is true.

Explanation of Solution

The columns of $\underset{\mathcal{C}\leftarrow \mathcal{B}}{P}$ are linearly independent because they are the coordinate vectors of the linearly independent set.

The matrix $\underset{\mathcal{C}\leftarrow \mathcal{B}}{P}$ is a square matrix thus; it must be an invertible matrix.

Hence, the statement is true.

To determine

To find: Whether the statement “If $\mathcal{B}=\left\{b_1,\dots ,b_n\right\}$ and $\mathcal{C}=\left\{c_1,\dots ,c_n\right\}$ are bases for a vector space V, then the $j$ th column of the change-of-coordinates matrix $\underset{\mathcal{C}\leftarrow \mathcal{B}}{P}$ is the coordinate vector ${\left[c_j\right]}_{\mathcal{B}}$” is true or false.

Answer to Problem 1SE

The statement is false.

Explanation of Solution

The jth column of the change-of-coordinates matrix $\underset{\mathcal{C}\leftarrow \mathcal{B}}{P}$ is ${\left[b_j\right]}_C$.

Hence, the statement is false.