
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
8th Edition
ISBN: 9781337798396
Author: SMITH
Publisher: CENGAGE LEARNING - CONSIGNMENT
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 39, Problem 1A
Use the Table of BlockThicknesses of a Customary Gage Block Set under the heading "Description of Gage Blocks" in Unit 37 to determine a combination of gage blocks for 3.7642".
Expert Solution & Answer
To determine
The combination of gage block.
Answer to Problem 1A
The combination of blocks are
Explanation of Solution
Given:
Dimension is
Calculation:
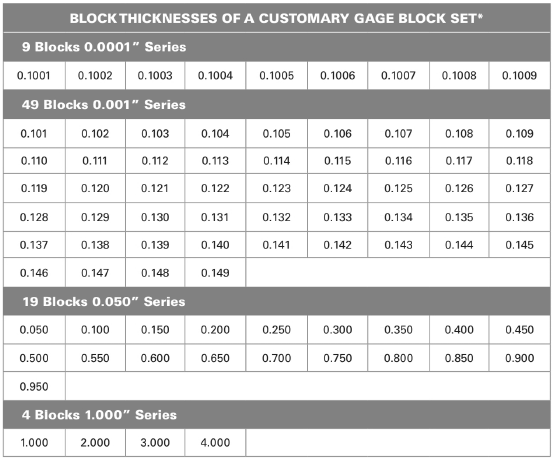
From above table:
The combination of the blocks are
Add all the dimensions of the blocks.
Thus, the combination of blocks are
Conclusion:
The combination of blocks are
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
-
Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p − 1)/2
multiple of n, i.e.
n mod p, 2n mod p, ...,
p-1
2
-n mod p.
Let T be the subset of S consisting of those residues which exceed p/2.
Find the set T, and hence compute the Legendre symbol (7|23).
23
32
how come?
The first 11 multiples of 7 reduced mod 23 are
7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8.
The set T is the subset of these residues exceeding
So T = {12, 14, 17, 19, 21}.
By Gauss' lemma (Apostol Theorem 9.6),
(7|23) = (−1)|T| = (−1)5 = −1.
Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p-1)/2
multiple of n, i.e.
n mod p, 2n mod p, ...,
2
p-1
-n mod p.
Let T be the subset of S consisting of those residues which exceed p/2.
Find the set T, and hence compute the Legendre symbol (7|23).
The first 11 multiples of 7 reduced mod 23 are
7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8.
23
The set T is the subset of these residues exceeding
2°
So T = {12, 14, 17, 19, 21}.
By Gauss' lemma (Apostol Theorem 9.6),
(7|23) = (−1)|T| = (−1)5 = −1.
how come?
Shading a Venn diagram with 3 sets: Unions, intersections, and...
The Venn diagram shows sets A, B, C, and the universal set U.
Shade (CUA)' n B on the Venn diagram.
U
Explanation
Check
A-
B
Q Search
田
Chapter 39 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
Ch. 39 - Use the Table of BlockThicknesses of a Customary...Ch. 39 - Use a digital micrometer to measure the length and...Ch. 39 - Read the setting of the metric micrometer scale in...Ch. 39 - Use an electronic vernier caliper to measure the...Ch. 39 - Prob. 5ACh. 39 - 43 is 62% of what number? Round the answer to 2...Ch. 39 - Express each of the following problems as an...Ch. 39 - Express each of the following problems as an...Ch. 39 - Express each of the following problems as an...Ch. 39 - Express each of the following problems as an...
Ch. 39 - Express each of the following problems as an...Ch. 39 - Express each of the following problems as an...Ch. 39 - Express each of the following problems as an...Ch. 39 - In the part shown in Figure 39-9, all dimensions...Ch. 39 - Find the distance between the indicated points of...Ch. 39 - What are the lengths of the following dimensions...Ch. 39 - Stock is removed from a block in two operations....Ch. 39 - Given: In Figure 39-12, s is the length of a side...Ch. 39 - Substitute the given numbers for letters and find...Ch. 39 - Prob. 20ACh. 39 - Prob. 21ACh. 39 - Prob. 22ACh. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...Ch. 39 - For Exercises 23 through 34, round the answers to...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Find all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forward
- Let A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective. why?(b) Determine if f is surjective. why?(c) Based upon (a) and (b), is f bijective? why?arrow_forwardLet f:R->R be defined by f(x)=x^(3)+5.(a) Determine if f is injective.(b) Determine if f is surjective. (c) Based upon (a) and (b), is f bijective?arrow_forward
- 1 S 0 sin(lnx) x² - 1 Inx dxarrow_forward2 6. Modelling. Suppose that we have two tanks (A and B) between which a mixture of brine flows. Tank A contains 200 liters of water in which 50 kilograms of salt has been dissolved and Tank B contains 100 liters of pure water. Water containing 1kg of salt per liter is pumped into Tank A at the rate of 5 liters per minute. Brine mixture is pumped into Tank A from Tank B at the rate of 3 liters per minute and brine mixture is pumped from Tank A into Tank B at the rate of 8 liters per minute. Brine is drained from Tank B at a rate of 5 liters per minute. (a) Draw and carefully label a picture of the situation, including both tanks and the flow of brine between them. JankA 1ks of Salt Slits Pump EL Brine mit tark A from tank 13 Tank 13 k 3L zooliters of Ico liters of water with pure water. Saky salt → 777 disslore inside Brine mix is pumped from tank A to B of 82 Brine drainen min by Gf salt (b) Assume all brine mixtures are well-stirred. If we let t be the time in minutes, let x(t) 1ks…arrow_forwardNo chatgpt plsarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Sequences and Series Introduction; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=m5Yn4BdpOV0;License: Standard YouTube License, CC-BY
Introduction to sequences; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=VG9ft4_dK24;License: Standard YouTube License, CC-BY