
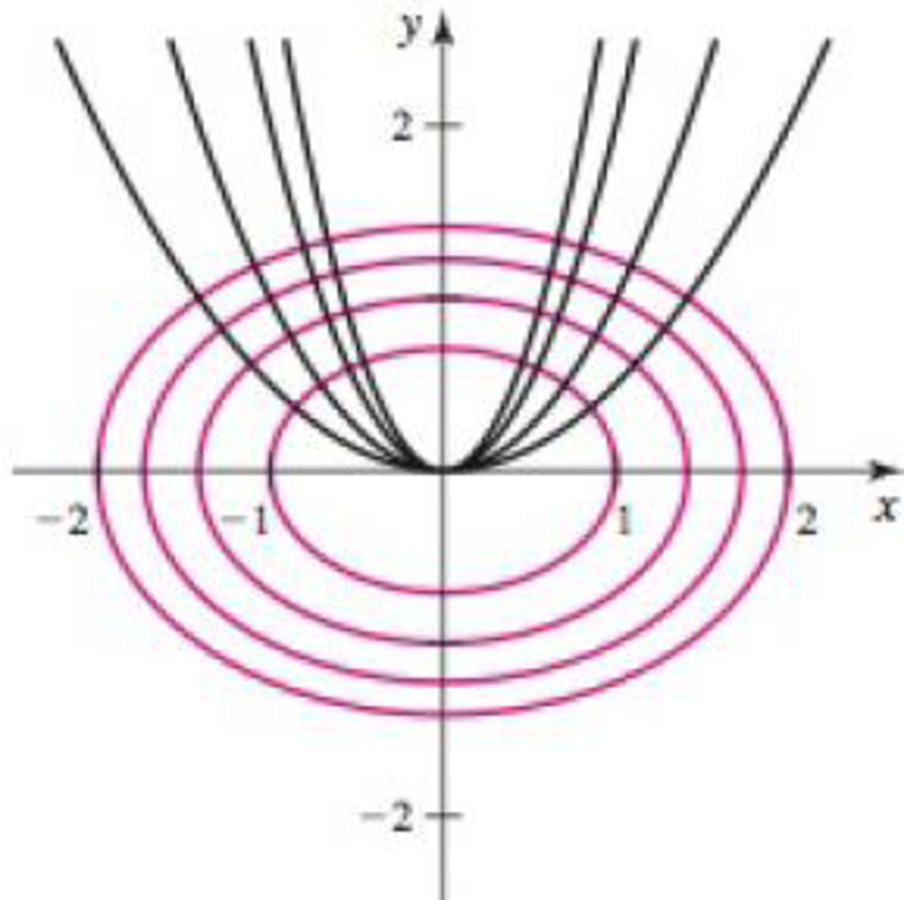
Orthogonal trajectories Two curves are orthogonal to each other if their tangent lines are perpendicular at each point of intersection (recall that two lines are perpendicular to each other if their slopes are negative reciprocals). A family of curves forms orthogonal trajectories with another family of curves if each curve in one family is orthogonal to each curve in the other family. For example, the parabolas y = cx2 form orthogonal trajectories with the family of ellipses x2 + 2y2 = k, where c and k are constants (see figure).
Find dy/dx for each equation of the following pairs. Use the derivatives to explain why the families of curves form orthogonal trajectories.
81. xy = a; x2 − y2 = b, where a and b are constants
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Single Variable Calculus: Early Transcendentals & Student Solutions Manual, Single Variable for Calculus: Early Transcendentals & MyLab Math -- Valuepack Access Card Package
Additional Math Textbook Solutions
Elementary Statistics
Thinking Mathematically (6th Edition)
Pre-Algebra Student Edition
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Algebra and Trigonometry (6th Edition)
- Find the indefinite integral by making a change of variables. (Remember the constant of integration.) √(x+4) 4)√6-x dxarrow_forwarda -> f(x) = f(x) = [x] show that whether f is continuous function or not(by using theorem) Muslim_mathsarrow_forwardUse Green's Theorem to evaluate F. dr, where F = (√+4y, 2x + √√) and C consists of the arc of the curve y = 4x - x² from (0,0) to (4,0) and the line segment from (4,0) to (0,0).arrow_forward
- Evaluate F. dr where F(x, y, z) = (2yz cos(xyz), 2xzcos(xyz), 2xy cos(xyz)) and C is the line π 1 1 segment starting at the point (8, ' and ending at the point (3, 2 3'6arrow_forwardCan you help me find the result of an integral + a 炉[メをメ +炉なarrow_forward2 a Can you help me find the result of an integral a 아 x² dxarrow_forward
- Please help me with this question as I want to know how can I perform the partial fraction decompostion on this alebgric equation to find the time-domain of y(t)arrow_forwardPlease help me with this question as I want to know how can I perform the partial fraction on this alebgric equation to find the time-domain of y(t)arrow_forwardEvaluate F³ - dr where ♬ = (4z, -4y, x), and C' is given by (t) = (sin(t), t, cos(t)), 0≤t≤ñ .arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
