Chapter 3.8, Problem 80E

Orthogonal trajectories Two curves are orthogonal to each other if their tangent lines are perpendicular at each point of intersection (recall that two lines are perpendicular to each other if their slopes are negative reciprocals). A family of curves forms orthogonal trajectories with another family of curves if each curve in one family is orthogonal to each curve in the other family. For example, the parabolas y = cx² form orthogonal trajectories with the family of ellipses x² + 2y² = k, where c and k are constants (see figure).

Find dy/dx for each equation of the following pairs. Use the derivatives to explain why the families of curves form orthogonal trajectories.

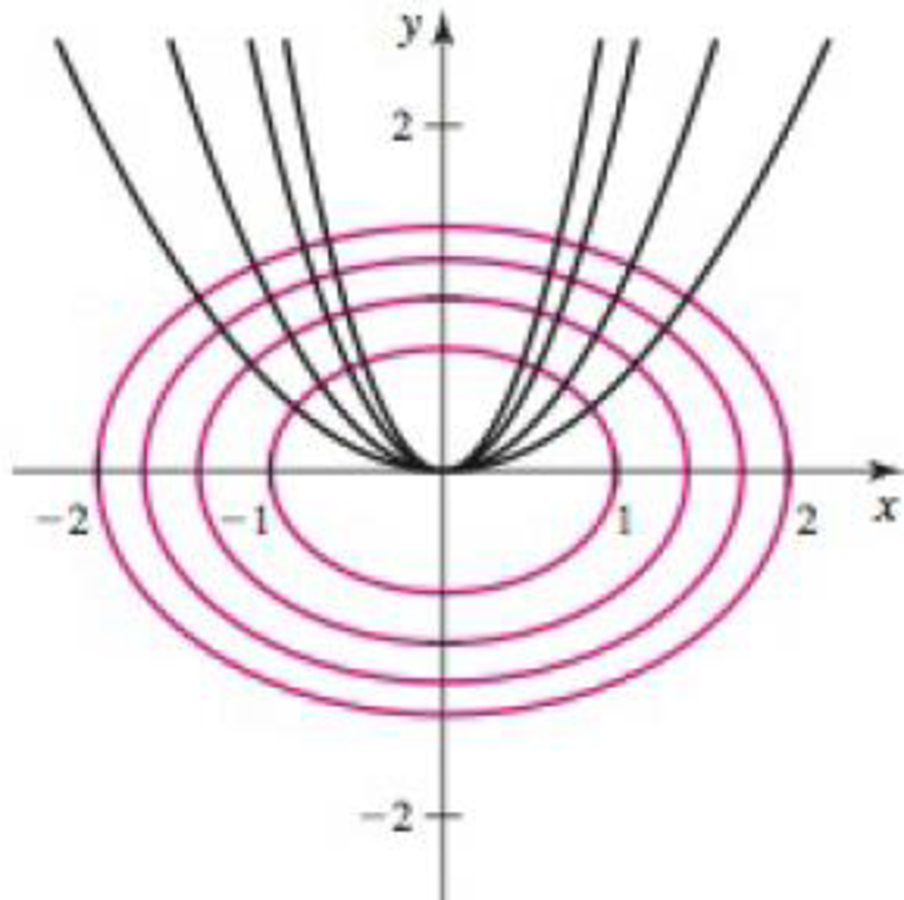
80. y = cx²; x² + 2y² = k, where c and k are constants