
Concept explainers
In Figure P36.10 (not to scale), let L = 1.20 m and d = 0.120 mm and assume the slit system is illuminated with monochromatic 500-nm light. Calculate the phase difference between the two wave fronts arriving at P when (a) θ = 0.500° and (b) y = 5.00 mm. (c) What is the value of θ for which the phase difference is 0.333 rad? (d) What is the value of θ for which the path difference is λ/4?
Figure P36.10
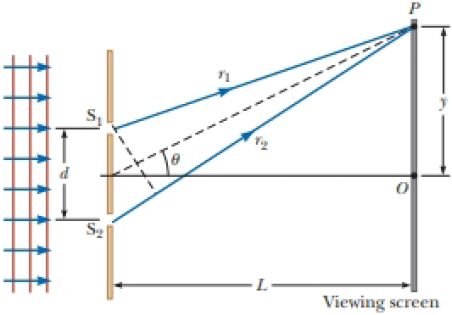
(a)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is 0.120 mm and the distance between the slit and screen is 1.20 m and wavelength of light is 500 nm.
The given diagram is shown below.
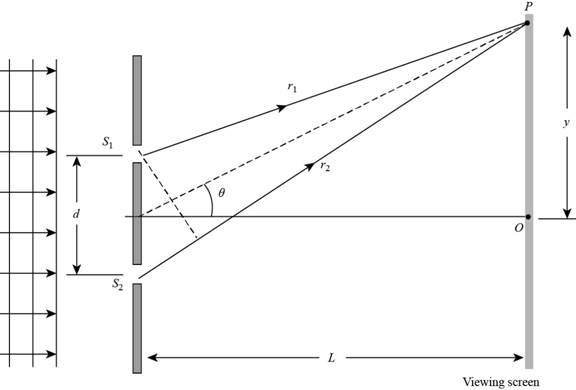
Figure 1
The formula to calculate the phase difference is,
ϕ=2πλdsin θ
Here,
λ is the wavelength.
d is the separation between the slits.
θ is the angle between the point P and horizontal.
Substitute 0.120 mm for d, 0.500° for θ, 500 nm for λ, in the above formula as,
ϕ=2πλdsin θ=2π(500 nm×10−9 m1 nm)(.120 mm×10−3 m1 mm)sin (0.500°)=13.2 radian
Conclusion:
Therefore, the phase difference between the two waves fronts arriving at P when θ=0.500° is 13.2 radian
(b)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is 0.120 mm and the distance between the slit and screen is 1.20 m and wavelength of light is 6.28 radian.
The formula to calculate the phase difference is,
ϕ=2πλdsin θ
Here,
λ is the wavelength.
d is the separation between the slits.
θ is the angle between the point P and horizontal.
From the right angle triangle sin θ is
sin θ=perpendicular hypotenuse=yL
Here,
y is the distance from O to P.
L is the distance between slit and screen.
Substitute yL for sin θ in the above formula as,
ϕ=2πλdsin θ=2πλd(yL)
Substitute 0.120 mm for d, 500 nm for λ, 1.20 m for L, 5.00 mm for y in the above formula as,
ϕ=2πλdsin θ=2π(500 nm×10−9 m1 nm)(.120 mm×10−3 m1 mm)(5.00 mm×10-3 m1 mm1.20 m)=6.28 radian
Conclusion:
Therefore, the phase difference between the two waves fronts arriving at P when y=5.00 mm is 6.28 radian
(c)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is 0.120 mm and the distance between the slit and screen is 1.20 m and wavelength of light is 6.28 radian, phase difference is 0.33 radian
The formula to calculate the phase difference is,
ϕ=2πλdsin θ
Here,
λ is the wavelength.
d is the separation between the slits.
θ is the angle between the point P and horizontal.
Rearrange the above formula to find θ is,
ϕ=2πλdsin θsin θ=λϕ2πdθ=sin−1 (λϕ2πd)
Substitute 0.120 mm for d, 500 nm for λ, 0.33 radian for ϕ in the above formula as,
θ=sin−1 (λϕ2πd)=sin−1 (500 nm×10−9 mm1 mm(0.33 radian)2π(0.120 mm×10−3 m1 mm))=1.27×10−2 degree
Conclusion:
Therefore, the value of θ is 1.27×10−2 degree.
(d)
Answer to Problem 37.18P
Explanation of Solution
Given info: The separation between the slits is 0.120 mm and the distance between the slit and screen is 1.20 m and wavelength of light is 6.28 radian, path difference is λ4
The formula to calculate the phase difference is,
ϕ=2πλdsin θ (1)
Here,
λ is the wavelength.
d is the separation between the slits.
θ is the angle between the point P and horizontal.
The path difference is λ4 as,
dsin θ=λ4
Substitute λ4 for dsin θ in the above formula as,
ϕ=2πλdsin θ=2πλ(λ4)=π2
Rearrange the equation (1) to find θ as,
θ=sin−1 (λϕ2πd)
Substitute 0.120 mm for d, 500 nm for λ, π2 for ϕ in the above formula as,
θ=sin−1 (λ(π2)2πd)=sin−1 (λ4d)=sin−1 (500 nm×10−9 mm1 mm4(0.120 mm×10−3 m1 mm))=5.97×10−2 degree
Conclusion:
Therefore, the value of θ is. 5.97×10−2 degree.
Want to see more full solutions like this?
Chapter 37 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- 2). How much energy is stored in the 50-μF capacitor when Va - V₁ = 22V? 25 µF b 25 µF 50 µFarrow_forward9). A series RC circuit has a time constant of 1.0 s. The battery has a voltage of 50 V and the maximum current just after closing the switch is 500 mA. The capacitor is initially uncharged. What is the charge on the capacitor 2.0 s after the switch is closed? R 50 V a. 0.43 C b. 0 66 C c. 0.86 C d. 0.99 C Carrow_forward1). Determine the equivalent capacitance of the combination shown when C = 12 pF. +11/20 2C C Carrow_forward
- 3). When a capacitor has a charge of magnitude 80 μC on each plate the potential difference across the plates is 16 V. How much energy is stored in this capacitor when the potential difference across its plates is 42 V? a. 1.0 mJ b. 4.4 mJ c. 3.2 mJ d. 1.4 mJ e. 1.7 mJarrow_forward5). A conductor of radius r, length & and resistivity p has resistance R. It is melted down and formed into a new conductor, also cylindrical, with one fourth the length of the original conductor. The resistance of the new conductor is a. 1 R 161 b. 1 R C. R d. 4R e. 16Rarrow_forward8). Determine the magnitude and sense (direction) of the current in the 10-Q2 resistor when I = 1.8 A. 30 V L 50 V 10 Ω 20 Ω a. 1.6 A right to left b. 1.6 A left to right C. 1.2 A right to left d. 1.2 A left to right e. 1.8 A left to right R PGarrow_forward
- 7). Determine the current in the 10-V emf. 5.0 0 w 10 V 5.0 0 15 V 5.0 Ω a. 2.3 A b. 2.7 A c. 1.3 A d. 0.30 A e. 2.5 Aarrow_forward4). What is the resistance of a wire made of a material with a resistivity of 3.2 is 2.5 m and its diameter is 0.50 mm? a. 0.16 Ω b. 0.10 2 C. c. 1.28 Ω d. 0.41 2 e. 0.81 2 108 m if its lengtharrow_forwardA flat circular coil with 135 turns, a radius of 2.28 x 10-2 m, and a resistance of 0.618 is exposed to an external magnetic field that is directed perpendicular to the plane of the coil. The magnitude of the external magnetic field is changing at a rate of AB/At = 0.615 T/s, thereby inducing a current in the coil. Find the magnitude of the magnetic field at the center of the coil that is produced by the induced current. Numberarrow_forward
- please solve the question attachedarrow_forwardSketch a sine wave depicting 3 seconds of wave activity for a 5 Hz tone. Sketch the resulting complex wave form that results from the combination of the following two waves. Is this wave periodic or aperiodic? USE GRAPH PAPER!arrow_forwardRequired information A bungee jumper leaps from a bridge and undergoes a series of oscillations. Assume g = 9.78 m/s². If a 60.0-kg jumper uses a bungee cord that has an unstretched length of 30.1 m and she jumps from a height of 45.2 m above a river, coming to rest just a few centimeters above the water surface on the first downward descent, what is the period of the oscillations? Assume the bungee cord follows Hooke's law.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax





