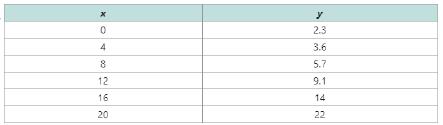
Problem 1SP: a. Given T=78+272ekt,solvefork. b. Given S=9020lnt+1,solvefort. Problem 2SP: Suppose that $10,000 is invested and at the end of 5 yr, the value of the account is $13,771.28. Use... Problem 3SP: On January 1, 2000, the population of Texas was approximately 21 million. On January 1, 2010, the... Problem 4SP: a. Given Pt=10,00020.4t, write the rule for this function using base e. b. Find the function value... Problem 5SP: Use the function Qt=Q0e0.000121t to determine the age of a piece of wood that has 42 of its... Problem 6SP: The score on a test of dexterity is by Pt=1001+19e0.354x , where x is the number of times the is... Problem 7SP: For the given data, a. Graph the data points. b. Use a graphing utility to find a model form y=abx... Problem 8SP: For the given data, a. Graph the data points. b. Use a graphing utility to find a model of the form... Problem 1PE: If k0, the equation y=y0ekt is a model for exponential (growth/decay), whereas if k0, the equation... Problem 2PE: A function defined by y=abx can be written in terms of an exponential function base e as . Problem 3PE: A function defined by y=c1+aebt is called a growth model and imposes a limiting value on y. Problem 4PE: Given a logistic function y=c1+aebt , the limiting value of y is . Problem 5PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) Q=Q0ektforkusedinchemistry Problem 6PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) N=N0e0.025tfortusedinchemistry Problem 7PE: For Exercises 5-14, solve for the indicated variable. (See Example 1)... Problem 8PE: For Exercises 5-14, solve for the indicated variable. (See Example 1)... Problem 9PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) pH=logH+forH+usedinchemistry Problem 10PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) L=10logII0forIusedinmedicine Problem 11PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) A=P1+rtfortusedinfinance Problem 12PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) A=Pertforrusedinfinance Problem 13PE: For Exercises 5-14, solve for the indicated variable. (See Example 1) InkA=ERTforkusedinchemistry Problem 14PE Problem 15PE: Suppose that $12,000 is invested in a bond fund and the account grows to $14,309.26 in 4 yr. (See... Problem 16PE: Suppose that $50,000 from a retirement account is invested in a large cap stock fund. After 20 yr.... Problem 17PE: Suppose that P dollars in principal is invested in an account earning 3.2 interest compounded... Problem 18PE: Suppose that P dollars in principal is invested in an account earning 2.1 interest compounded... Problem 19PE: The populations of two countries are given for January 1, 2000, and for January 1, 2010. a. Write a... Problem 20PE: The populations of two countries are given for January 1, 2000, and for January 1, 2010. a. Write a... Problem 21PE: A function of the form Pt=abt represents the population (in millions) of the given country t years... Problem 22PE: A function of the form Pt=abt represents the population (in millions) of the given country t years... Problem 23PE Problem 24PE: For Exercises 23-24, refer to the model Qt=Q0e0.000121t used in Example 5 for radiocarbon dating. At... Problem 25PE: The isotope of plutonium 238Pu is used to make thermoelectric power sources for spacecraft. Suppose... Problem 26PE: Technetium-99 99mTc is a radionuclide used widely in nuclear medicine.99mTc is combined with another... Problem 27PE: Fluorodeoxyglucose is a derivative of glucose that contains the radionuclide fluorine-18 18F. A... Problem 28PE: Painful bone metastases are common in advanced prostate cancer. Physicians often order treatment... Problem 29PE: Two million E. coli bacteria are present in a laboratory culture. An antibacterial agent is... Problem 30PE: The half-life of radium-226 is 1620 yr. Given a sample of 1 g of radium-226, the quantity left Qt... Problem 31PE: The population of the United States Pt (in millions) since January 1, 1900, can be approximated by... Problem 32PE: The population of Canada Pt (in millions) since January 1, 1900, can be approximated by... Problem 33PE: The number of computers Nt (in millions) infected by a computer virus can be approximated by... Problem 34PE: After a new product is launched the cumulative sales Stin$1000t weeks after launch is given by... Problem 35PE: For Exercises 35-38, a graph of data is given. From visual inspection, which model would best fit... Problem 36PE: For Exercises 35-38, a graph of data is given. From visual inspection, which model would best fit... Problem 37PE: For Exercises 35-38, a graph of data is given. From visual inspection, which model would best fit... Problem 38PE: For Exercises 35-38, a graph of data is given. From visual inspection, which model would best fit... Problem 39PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 40PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 41PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 42PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 43PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 44PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 45PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 46PE: For Exercises 39-46, a table of data is given. a. Graph the points and from visual inspection,... Problem 47PE: During a recent outbreak of Ebola in western Africa, the cumulative number of cases y was reported t... Problem 48PE: The monthly costs for a small company to do business has been increasing over time due in part to... Problem 49PE: The age of a tree t (in yr) and its corresponding height Ht are given in the table. (See Example 8)... Problem 50PE: The sales of a book tend to increase over the short-term as word-of-mouth makes the book “catch... Problem 51PE: A van is purchased new for $29,200. a. Write a linear function of the form y=mt+b to represent the... Problem 52PE: A delivery truck is purchased new for $54,000 . a. Write a linear function of the form y=mt+b to... Problem 53PE: Why is it important to graph a set of data before trying to find an equation or function to model... Problem 54PE Problem 55PE Problem 56PE: Explain how to convert an exponential expression bt to an exponential expression base e. Problem 57PE Problem 58PE: Suppose that a population follows a logistic growth pattern, with a limiting population N. If the... format_list_bulleted


 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw HillAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning

