EBK MATHEMATICS FOR MACHINE TECHNOLOGY
8th Edition
ISBN: 9781337798396
Author: SMITH
Publisher: CENGAGE LEARNING - CONSIGNMENT
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 36, Problem 2A
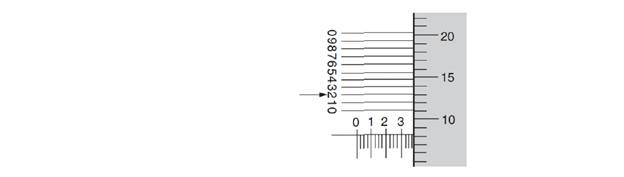
Read the setting on this customary vernier micrometer scale graduated to 0.0001". The vernier, thimble, and barrel scales are shown in flattened view.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Prove that
f: f
→> R
16
One-to-
one.
Use mathematical induction to prove the following statement: For all natural numbers n, 5 divides 6^n - 1 (show every step in detail)
Use mathematical induction to prove the following statement: For all natural numbers n, 5 divides 6^n - 1
Chapter 36 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
Ch. 36 - Read the setting of this metric micrometer scale...Ch. 36 - Read the setting on this customary vernier...Ch. 36 - Use a digital vernier caliper to measure the...Ch. 36 - Read the decimal-inch vernier caliper measurement...Ch. 36 - Express 2.0276 meters as centimeters.Ch. 36 - Prob. 6ACh. 36 - Prob. 7ACh. 36 - Use a digital micrometer to measure the indicated...Ch. 36 - Prob. 9ACh. 36 - Prob. 10A
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- the set of all preimages of 2 isarrow_forwardWhich diagram(s) represent the following relationships An injective function from A to B? A surjective function from A to B? An injective function from B to A? A surjective function from B to A?arrow_forwardDetermine if each statement is true or false. If the statement is false, provide a brief explanation: a) There exists x = R such that √x2 = -x. b) Let A = {x = ZIx = 1 (mod 3)} and B = {x = ZIx is odd}. Then A and B are disjoint. c) Let A and B be subsets of a universal set U. If x = A and x/ € A - B,then x = An B.| E d) Let f : RR be defined by f (x) = 1 x + 2 1. Then f is surjective.arrow_forward
- Write the negation of the definition of an injective functionarrow_forwardLet U= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {xeU Ix is a multiple of 3}, and B = {x = UIx = 0 (mod 2)}. Use the roster method to list all elements in each of the following sets: a) A, b) B, c) A u B, d) B – A, e) A^cn Barrow_forwardThe function f is; Injective (only), Surjective (only), Bijective, or none? show workarrow_forward
- For each a Є Z, if a ‡0 (mod 3), then a² = 1 (mod 3).arrow_forwardfind: f(3)=? , and the set of all preimages of 2 is ?arrow_forwardConstruct tables showing the values of alI the Dirichlet characters mod k fork = 8,9, and 10. (please show me result in a table and the equation in mathematical format.)arrow_forward
- Example: For what odd primes p is 11 a quadratic residue modulo p? Solution: This is really asking "when is (11 | p) =1?" First, 11 = 3 (mod 4). To use LQR, consider two cases p = 1 or 3 (mod 4): p=1 We have 1 = (11 | p) = (p | 11), so p is a quadratic residue modulo 11. By brute force: 121, 224, 3² = 9, 4² = 5, 5² = 3 (mod 11) so the quadratic residues mod 11 are 1,3,4,5,9. Using CRT for p = 1 (mod 4) & p = 1,3,4,5,9 (mod 11). p = 1 (mod 4) & p = 1 (mod 11 gives p 1 (mod 44). p = 1 (mod 4) & p = 3 (mod 11) gives p25 (mod 44). p = 1 (mod 4) & p = 4 (mod 11) gives p=37 (mod 44). p = 1 (mod 4) & p = 5 (mod 11) gives p 5 (mod 44). p = 1 (mod 4) & p=9 (mod 11) gives p 9 (mod 44). So p =1,5,9,25,37 (mod 44).arrow_forwardhow to construct the following same table?arrow_forwardplease work out more details give the solution.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License