
Concept explainers
A converging lens has a focal length of 10.0 cm. Construct accurate ray diagrams for object distances of (i) 20.0 cm and (ii) 5.00 cm. (a) From your ray diagrams, determine the location of each image. (b) Is the image real or virtual? (c) Is the image upright or inverted? (d) What is the magnification of the image? (c) Compare your results with the values found algebraically. (f) Comment on difficulties in constructing the graph that could lead to differences between the graphical and algebraic answers.
(i)
To draw: The ray diagram for the given focal lengthy of the lens and the given object distance.
Answer to Problem 26P
Explanation of Solution
Introduction:
In a ray diagram in the case of lens or mirror the image is formed where two at least refracted or reflected rays coincide with each other.
Explanation:
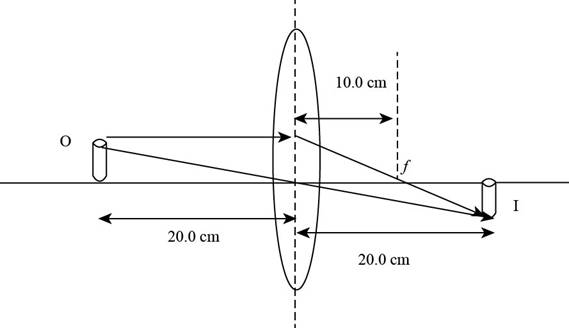
Given info: The position of object is at
The ray diagram is shown in the figure below.
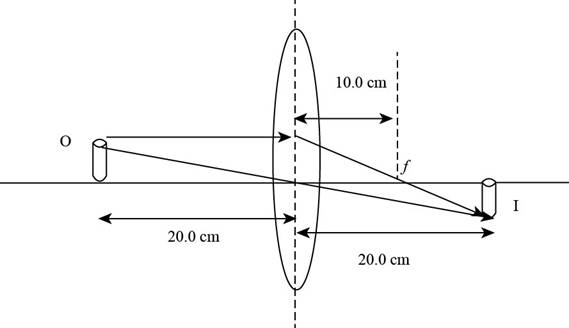
Figure (1)
(ii)
To draw: The ray diagram for the given focal length of the lens and the given object distance.
Answer to Problem 26P
Explanation of Solution
Introduction:
In a ray diagram in the case of lens or mirror the image is formed where two at least refracted or reflected rays coincide with each other.
Explanation:
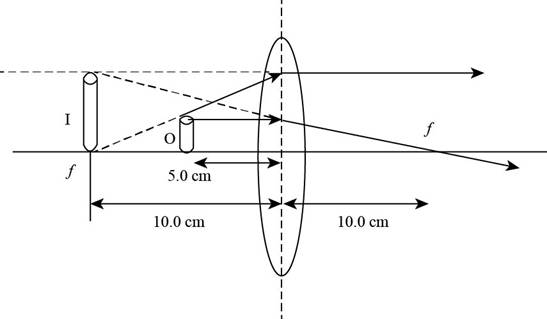
Given info: The position of object is at
The ray diagram is shown in the figure below.
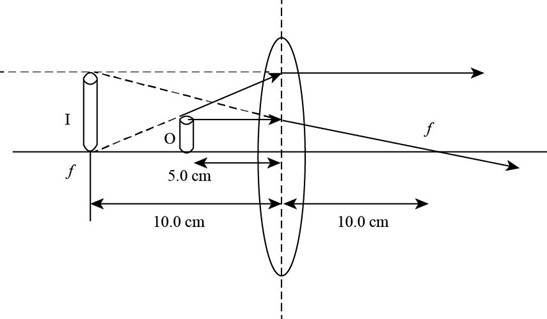
Figure (2)
(a)
Answer to Problem 26P
Explanation of Solution
From Figure (1), it is evident that the image is formed on the rear end of the lens and the image distance measured is
From Figure (2), the image is formed at
Conclusion:
Therefore, the measured distance for the image for the case when object is at
(b)
Answer to Problem 26P
Explanation of Solution
From Figure (1), it is evident that the image is formed on the rear side and is real and the images formed at the back side of the lens are real.
From Figure (2), the image is formed at
Conclusion:
The images formed by the lens in front of it are virtual and erect and images formed on the back side are real and inverted. Hence, image formed by the object kept at.
(c)
Answer to Problem 26P
Explanation of Solution
From Figure (1), it is evident that the image is formed on the rear side and is real. and
the real images are always inverted
From Figure (2), the image is formed at
The virtual images are always upright.
Conclusion:
Therefore, the images formed by the lens in front of it are virtual and erect and images formed on the back side are real and inverted. Hence, image formed by the object kept at.
(d)
Answer to Problem 26P
Explanation of Solution
Formula to calculate the magnification is
For the object at
For the object at the distance of
Conclusion:
Therefore, for the case of object at
(e)
Answer to Problem 26P
Explanation of Solution
Given Info: The focal length of the give lens is
From Figure (1) the image distance for the object at
For algebraic calculation, the formula for the image distance is,
Here,
Substitute
Form figure (1) the magnification is
Formula to calculate the magnification of the image
Here
Substitute
From figure (2) the image distance is
From equation (4) formula to calculate the image distance is,
Substitute
The image distance is
From equation (6) the formula to calculate the magnification is,
Substitute
From equation (6) and equation (7) it is evident that for the case of object at
From equation (8) and (9) the image distance and magnification is same for the ray diagram and the algebraic case when the object is
Conclusion:
Therefore, the result for the ray diagrams and algebraic calculations are same.
(f)
Answer to Problem 26P
Explanation of Solution
While drawing the graph the possible errors are human hand errors, parallax errors and scale measurement errors.
Human Hand Errors are while making the ray diagrams the rays might not converge with extreme precision. Parallax error/Human eye errors occur due to human eye. Scale errors are during the scale measurement.
Conclusion:
Therefore, the three most common errors that can lead to difficulties in constructing the graph which might lead to change the algebraic and graphical values are human hand errors, parallax errors and Scale errors.
Want to see more full solutions like this?
Chapter 35 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- You are standing a distance x = 1.75 m away from this mirror. The object you are looking at is y = 0.29 m from the mirror. The angle of incidence is θ = 30°. What is the exact distance from you to the image?arrow_forwardFor each of the actions depicted below, a magnet and/or metal loop moves with velocity v→ (v→ is constant and has the same magnitude in all parts). Determine whether a current is induced in the metal loop. If so, indicate the direction of the current in the loop, either clockwise or counterclockwise when seen from the right of the loop. The axis of the magnet is lined up with the center of the loop. For the action depicted in (Figure 5), indicate the direction of the induced current in the loop (clockwise, counterclockwise or zero, when seen from the right of the loop). I know that the current is clockwise, I just dont understand why. Please fully explain why it's clockwise, Thank youarrow_forwardA planar double pendulum consists of two point masses \[m_1 = 1.00~\mathrm{kg}, \qquad m_2 = 1.00~\mathrm{kg}\]connected by massless, rigid rods of lengths \[L_1 = 1.00~\mathrm{m}, \qquad L_2 = 1.20~\mathrm{m}.\]The upper rod is hinged to a fixed pivot; gravity acts vertically downward with\[g = 9.81~\mathrm{m\,s^{-2}}.\]Define the generalized coordinates \(\theta_1,\theta_2\) as the angles each rod makes with thedownward vertical (positive anticlockwise, measured in radians unless stated otherwise).At \(t=0\) the system is released from rest with \[\theta_1(0)=120^{\circ}, \qquad\theta_2(0)=-10^{\circ}, \qquad\dot{\theta}_1(0)=\dot{\theta}_2(0)=0 .\]Using the exact nonlinear equations of motion (no small-angle or planar-pendulumapproximations) and assuming the rods never stretch or slip, determine the angle\(\theta_2\) at the instant\[t = 10.0~\mathrm{s}.\]Give the result in degrees, in the interval \((-180^{\circ},180^{\circ}]\).arrow_forward
- What are the expected readings of the ammeter and voltmeter for the circuit in the figure below? (R = 5.60 Ω, ΔV = 6.30 V) ammeter I =arrow_forwardsimple diagram to illustrate the setup for each law- coulombs law and biot savart lawarrow_forwardA circular coil with 100 turns and a radius of 0.05 m is placed in a magnetic field that changes at auniform rate from 0.2 T to 0.8 T in 0.1 seconds. The plane of the coil is perpendicular to the field.• Calculate the induced electric field in the coil.• Calculate the current density in the coil given its conductivity σ.arrow_forward
- An L-C circuit has an inductance of 0.410 H and a capacitance of 0.250 nF . During the current oscillations, the maximum current in the inductor is 1.80 A . What is the maximum energy Emax stored in the capacitor at any time during the current oscillations? How many times per second does the capacitor contain the amount of energy found in part A? Please show all steps.arrow_forwardA long, straight wire carries a current of 10 A along what we’ll define to the be x-axis. A square loopin the x-y plane with side length 0.1 m is placed near the wire such that its closest side is parallel tothe wire and 0.05 m away.• Calculate the magnetic flux through the loop using Ampere’s law.arrow_forwardDescribe the motion of a charged particle entering a uniform magnetic field at an angle to the fieldlines. Include a diagram showing the velocity vector, magnetic field lines, and the path of the particle.arrow_forward
- Discuss the differences between the Biot-Savart law and Coulomb’s law in terms of their applicationsand the physical quantities they describe.arrow_forwardExplain why Ampere’s law can be used to find the magnetic field inside a solenoid but not outside.arrow_forward3. An Atwood machine consists of two masses, mA and m B, which are connected by an inelastic cord of negligible mass that passes over a pulley. If the pulley has radius RO and moment of inertia I about its axle, determine the acceleration of the masses mA and m B, and compare to the situation where the moment of inertia of the pulley is ignored. Ignore friction at the axle O. Use angular momentum and torque in this solutionarrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





