
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
7th Edition
ISBN: 9780100548169
Author: SMITH
Publisher: YUZU
expand_more
expand_more
format_list_bulleted
Question
Chapter 35, Problem 1A
To determine
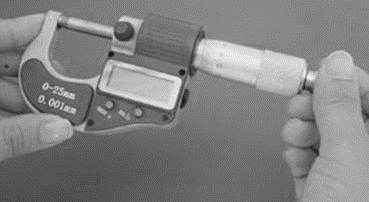
The thickness of the cover of a book measured with the help of digital micrometer.
Expert Solution & Answer
Explanation of Solution
Digital micrometers can be used to measure the linear dimensions such as length, diameter and thickness. The main components of a micrometer are frame, anvil, lock nut,thimble marks,ratchet stop, spindle, sleeve,display with LCD screen, units conversion key, and the key for turning ON and OFF.
The thickness of the book can be measured in the following steps.
- Dry all the surfaces of the micrometer and clean the surfaces with the help of cloth or a cloth soaked or dipped in the cleaning oil.
- The digital micrometer is to be closed completely and the thimble is to be turn in such a manner that the zero line aligns to the center line of sleeve.
- Now the ON/OFF button should be pressed on the digital micrometer. The zero reading on the digital micrometer means that the thickness of the book can be read directly.If the reading on the micrometer is not zero, the thimble and ratchet stop is to be adjusted so that it reads zero.
- The jaws of the digital micrometer are opened by carefully revolving ratchet of the micrometer.
- The cover of a book is placed inside the anvil of the micrometer. The micrometer anvil is kept vertically to the book thickness to be measured.
- The locknut on the digital micrometer are locked so that there is no further change in the reading of the digital micrometer.
- The result will vary depending on the type of cover used for measurement.
- The average thickness of the cover of a book is 0.1 mm.



Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
Question 1. Prove that the function f(x) = 2; f: (2,3] → R, is not uniformly
continuous on (2,3].
Consider the cones
K =
= {(x1, x2, x3) | € R³ :
X3
≥√√√2x² + 3x²
M =
= {(21,22,23)
(x1, x2, x3) Є R³: x3 >
+
2
3
Prove that M = K*.
Hint: Adapt the proof from the lecture notes for finding the dual of the Lorentz cone. Alternatively, prove the
formula (AL)* = (AT)-¹L*, for any cone LC R³ and any 3 × 3 nonsingular matrix A with real entries, where
AL = {Ax = R³ : x € L}, and apply it to the 3-dimensional Lorentz cone with an appropriately chosen matrix
A.
I am unable to solve part b.
Chapter 35 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
Ch. 35 - Prob. 1ACh. 35 - Read the settings of this metric vernier...Ch. 35 - Prob. 3ACh. 35 - Prob. 4ACh. 35 - Prob. 5ACh. 35 - Prob. 6ACh. 35 - Prob. 7ACh. 35 - Prob. 8ACh. 35 - Prob. 9ACh. 35 - Prob. 10A
Ch. 35 - Prob. 11ACh. 35 - Prob. 12ACh. 35 - Prob. 13ACh. 35 - Prob. 14ACh. 35 - Prob. 15ACh. 35 - Using the Table of Block Thicknesses for a...Ch. 35 - Prob. 17ACh. 35 - Prob. 18ACh. 35 - Prob. 19ACh. 35 - Prob. 20ACh. 35 - Prob. 21ACh. 35 - Prob. 22ACh. 35 - Prob. 23ACh. 35 - Prob. 24ACh. 35 - Prob. 25ACh. 35 - Prob. 26ACh. 35 - Prob. 27ACh. 35 - Prob. 28ACh. 35 - Prob. 29ACh. 35 - Prob. 30ACh. 35 - Using the Table of Block Thicknesses for a...Ch. 35 - Prob. 32ACh. 35 - Prob. 33ACh. 35 - Prob. 34ACh. 35 - Prob. 35ACh. 35 - Prob. 36ACh. 35 - Prob. 37ACh. 35 - Prob. 38ACh. 35 - Prob. 39ACh. 35 - Prob. 40ACh. 35 - Prob. 41ACh. 35 - Prob. 42ACh. 35 - Prob. 43ACh. 35 - Prob. 44ACh. 35 - Prob. 45ACh. 35 - Prob. 46ACh. 35 - Prob. 47ACh. 35 - Prob. 48ACh. 35 - Prob. 49ACh. 35 - Prob. 50ACh. 35 - Prob. 51ACh. 35 - Prob. 52ACh. 35 - Prob. 53ACh. 35 - Prob. 54ACh. 35 - Prob. 55A
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Let M = M₁U M₂ UM3 and K M₁ = {(x1, x2) ER²: 2 ≤ x ≤ 8, 2≤ x ≤8}, M₂ = {(x1, x2)™ € R² : 4 ≤ x₁ ≤ 6, 0 ≤ x2 ≤ 10}, M3 = {(x1, x2) Є R²: 0 ≤ x₁ ≤ 10, 4≤ x ≤ 6}, ¯ = cone {(1, 2), (1,3)†} ≤ R². (a) Determine the set E(M,K) of efficient points of M with respect to K. (b) Determine the set P(M, K) of properly efficient points of M with respect to K.arrow_forward5.17 An aluminum curtain wall panel 12 feet high is attached to large concrete columns (top and bottom) when the temperature is 65°F. No provision is made for differen- tial thermal movement vertically. Because of insulation between them, the sun heats up the wall panel to 120°F but the column to only 80°F. Determine the consequent compressive stress in the curtain wall. CONCRETE COLUMNS CONNECTIONS Stress= ALUMINUM WALL PANEL 12'-0"arrow_forward6.2 יך 4" 2" 2" Find the centroid of the following cross-sections and planes. X= Y=arrow_forward
- Find the directional derivative of the function at P in direction Varrow_forward6.4 49 Find the centroid of the following cross-sections and planes. X=_ Y= C15 XAO (CENTERED) KW14x90arrow_forward5.18 The steel rails of a continuous, straight railroad track are each 60 feet long and are laid with spaces be- tween their ends of 0.25 inch at 70°F. a. At what temperature will the rails touch end to end? b. What compressive stress will be produced in the rails if the temperature rises to 150°F? T= Stress= L= 60' 25 @T=70°Farrow_forward
- Strength of Materials Problems 5.16 A long concrete bearing wall has vertical expansion joints placed every 40 feet. Determine the required width of the gap in a joint if it is wide open at 20°F and just barely closed at 80°F. Assume α = 6 × 10-6/°F. Width= CONCRETE BEARING WALL EXPANSION JOINT 40' 40' 40' 293arrow_forwardCan you show me a step by step explanation please.arrow_forward9.7 Given the equations 0.5x₁-x2=-9.5 1.02x₁ - 2x2 = -18.8 (a) Solve graphically. (b) Compute the determinant. (c) On the basis of (a) and (b), what would you expect regarding the system's condition? (d) Solve by the elimination of unknowns. (e) Solve again, but with a modified slightly to 0.52. Interpret your results.arrow_forward
- 12.42 The steady-state distribution of temperature on a heated plate can be modeled by the Laplace equation, 0= FT T + 200°C 25°C 25°C T22 0°C T₁ T21 200°C FIGURE P12.42 75°C 75°C 00°C If the plate is represented by a series of nodes (Fig. P12.42), cen- tered finite-divided differences can be substituted for the second derivatives, which results in a system of linear algebraic equations. Use the Gauss-Seidel method to solve for the temperatures of the nodes in Fig. P12.42.arrow_forward9.22 Develop, debug, and test a program in either a high-level language or a macro language of your choice to solve a system of equations with Gauss-Jordan elimination without partial pivoting. Base the program on the pseudocode from Fig. 9.10. Test the program using the same system as in Prob. 9.18. Compute the total number of flops in your algorithm to verify Eq. 9.37. FIGURE 9.10 Pseudocode to implement the Gauss-Jordan algorithm with- out partial pivoting. SUB GaussJordan(aug, m, n, x) DOFOR k = 1, m d = aug(k, k) DOFOR j = 1, n aug(k, j) = aug(k, j)/d END DO DOFOR 1 = 1, m IF 1 % K THEN d = aug(i, k) DOFOR j = k, n aug(1, j) END DO aug(1, j) - d*aug(k, j) END IF END DO END DO DOFOR k = 1, m x(k) = aug(k, n) END DO END GaussJordanarrow_forward11.9 Recall from Prob. 10.8, that the following system of equations is designed to determine concentrations (the e's in g/m³) in a series of coupled reactors as a function of amount of mass input to each reactor (the right-hand sides are in g/day): 15c3cc33300 -3c18c26c3 = 1200 -4c₁₂+12c3 = 2400 Solve this problem with the Gauss-Seidel method to & = 5%.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL


Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Problems on Area and Circumference of Circle| Basics of Circle| Questions on Circle||BrainPanthers; Author: Brain Panthers;https://www.youtube.com/watch?v=RcNEL9OzcC0;License: Standard YouTube License, CC-BY