Chapter 3.4, Problem 2ES

Use Theorem 3.9 or Algorithm 3.3 to construct an approximating polynomial for the following data.

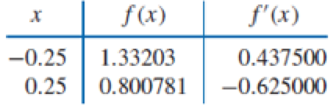
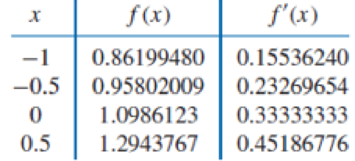
ALGORITHM 3.3

Hermite Interpolation

To obtain the coefficients of the Hermite interpolating polynomial H(x) on the (n + 1) distinct numbers x₀, …, x_n for the function f:

INPUT numbers x₀, x₁, …, x_n; values f (x₀), ... , f (x_n) and f′ (x₀), ... , f′ (x_n).

OUTPUT the numbers Q_{0, 0}, Q_{1, 1}, … , Q_{2n + 1, 2n + 1} where

$\begin{array}{l}H(x)=Q_{0,0}+Q_{1,1}\left(x-x_0\right)+Q_{2,2}{\left(x-x_0\right)}^2+Q_{3,3}{\left(x-x_0\right)}^2\left(x-x_1\right)\\ +Q_{4,4}{\left(x-x_0\right)}^2{\left(x-x_1\right)}^2+\cdots \\ +Q_{2n+1,2n+1}{\left(x-x_0\right)}^2{\left(x-x_1\right)}^2\cdots {\left(x-x_{n-1}\right)}^2\left(x-x_n\right).\end{array}$

Step 1 For i = 0, 1, … , n do Steps 2 and 3.

Step 2 $\begin{array}{l}Set{z}_{2i}=x_i;\\ \begin{array}{l}{z}_{2i+1}=x_i;\hfill \\ Q_{2i,0}=f\left(x_i\right);\hfill \\ Q_{2i+1,0}=f\left(x_i\right);\hfill \\ Q_{2i+1,1}=f^{\prime }\left(x_i\right).\hfill \end{array}\end{array}$

Step 3 If i ≠ 0 then set

$Q_{2i,1}=\frac{Q_{2i,0}-Q_{2i-1,0}}{z_{2i}-z_{2i-1}}.$

Step 4 For i = 2, 3, … , 2n + 1

for j = 2, 3, ... , i set $Q_{i,j}=\frac{Q_{i,j-1}-Q_{i-1,j-1}}{z_i-z_{i-j}}.$

Step 5 OUTPUT (Q_{0, 0}, Q_{1, 1}, … , Q_{2n + 1, 2n + 1});

STOP.

Theorem 3.9 If f ∈ C¹ [a, b] and x₀, …, x_n ∈ [a, b] are distinct, the unique polynomial of least degree agreeing with f and f′ at x₀, …, x_n is the Hermite polynomial of degree at most 2n + 1 given by

$H_{2n+1}(x)={\displaystyle \underset{j=0}{\overset{n}{\sum }}f}\left(x_j\right)H_{n,j}(x)+{\displaystyle \underset{j=0}{\overset{n}{\sum }}{f}^{\prime }}\left(x_j\right){\hat{H}}_{n,j}(x),$

where, for L_{n, j} (x) denoting the jth Lagrange coefficient polynomial of degree n, we have

$H_{n,j}(x)=\left[1-2\left(x-x_j\right){L^{\prime }}_{n,j}\left(x_j\right)\right]L_{n,j}^2(x)\text{ and }{\hat{H}}_{n,j}(x)=\left(x-x_j\right)L_{n,j}^2(x).$

Moreover, if f ∈ C^{2n + 2} [a, b], then

$f(x)=H_{2n+1}(x)+\frac{{\left(x-x_0\right)}^2\dots {\left(x-x_n\right)}^2}{(2n+2)!}{f}^{(2n+2)}(\xi (x)),$

for some (generally unknown) ξ(x) in the interval (a, b).