
To formulate a related decision problem for the independent-set problem and prove that it is NP-complete.
Explanation of Solution
Independent set of a graph G represents the set or collection of vertices that are not adjacent to one another. It is a concept in graph theory according to which there should not be any edge connecting the two vertices of a set.
- It is also known as a stable set in which an edge can have at most single endpoint in the graph.
- Thus, the vertices contained in the independent set represent the subset of the vertices of a graph.
Consider the figure or the graph given below containing an independent set of size 3:
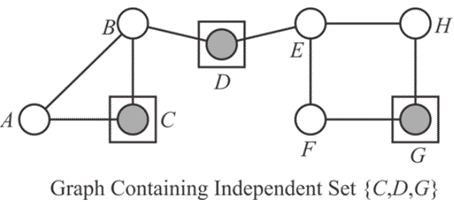
Consider a graph 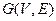 containing V vertices and set of edges E. Here, it is required to devise a decision problem for the independent−set problem and proving that it is NP-complete.
containing V vertices and set of edges E. Here, it is required to devise a decision problem for the independent−set problem and proving that it is NP-complete.
Decision problem:
- It is a way of asking the question in order to determine that whether a solution or answer of a particular question exists or not.
- It is a type of problem in a formal system in which the answer or solution of the problem comes out to be in two definite forms as either yes or no.
Consider the following example:
Graph coloring, Hamiltonian cycle or graph. Travelling salesperson Problem (TSP) is some of the common examples of the decision problems (all these can also be expressed as an optimization problem).
Now, it is also asked to show that independent set problem is NP complete.
NP Hard: To show that the problem is NP Hard, the concept of reducing or transforming the instance of the clique problem to an instance of an independent set S.
Consider the instance of the clique problem as  This problem is independent set problem having set
This problem is independent set problem having set  where
where 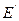 is the complement of E.
is the complement of E.
The set of vertices V represents a clique having size x is in the graph G only in case if V’ is an independent set of graph G’ having the size x and it is also following the fact that the construction of 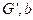 from
from 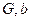 must be done in polynomial time.
must be done in polynomial time.
In this regard, it can be concluded that independent set problem is also NP hard. Thus it has been proved that an independent set problem is NP as well as NP-hard so it can be said that it is always NP complete.
To give an
Explanation of Solution
Given a black box subroutine to solve the decision problem defined in part (a) and a graph 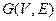
To implement the algorithm for solving the problem consider black box as 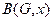
Algorithm:
//perform search operation
Step 1: start binary search on B to determine the maximum size 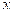 for the independent set.
for the independent set.
//initialization step.
Step 2: Set the independent set I to be an empty set.
Step 3: For each 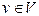
Construct 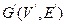 by removal of
by removal of 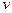 and its related edges from the graph
and its related edges from the graph 
Step 4: If 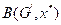
Set 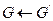
Else 
Here 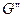 is obtained by removal of all the vertices which are connected to
is obtained by removal of all the vertices which are connected to 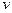 and the edges which are linked to it from the graph
and the edges which are linked to it from the graph 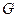
//end
Here, step 1 has a time complexity of 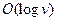
Step2: it has a time complexity of 
Step 3-4 : They have the number of iterations equal to 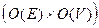
Hence it can be concluded that the time complexity is equal to 
To give an efficient algorithm to solve the independent-set problem when each vertex in G has degree 2.
Explanation of Solution
Given that the degree of the graph is 2, which implies that each vertex in the graph has a cardinality or degree 2.
Here, it is required to give an algorithm that can solve the independent set problem of a graph having degree 2.
Also, it is required to analyze the running time and the correctness of an algorithm.
Consider the graphs containing a simple cycle-
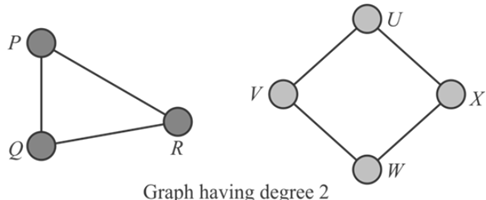
Thus, from the above graphs it can be observed that generally the graph containing the vertices of degree 2 is a simple cycle.
Therefore, the independent set problem is such a case can be achieved by initiating at any vertex and start choosing the alternate vertex on the cycle till the size obtained for the independent set to be 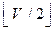
Hence, it can also be concluded that that the running time of the algorithm to solve the problem of independent set having V vertices, E edges and degree of each vertex as 2 is 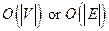
To give an algorithm to solve the independent set problem when G is bipartite.
Explanation of Solution
A bipartite graph commonly known as the biograph is an undirected graph whose vertex set can be partitioned or arranged into two disjoint sets that are independent.
It is possible to color this type of graph by using the two colors only so it is 2 colorable or bichromatic.
There are several applications of these graphs by using graphs like in case of matching problems.
For example:
Consider a bipartite graph given below containing two set of vertices 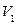 and
and 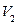 such that
such that 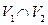
First find the maximum-matching of the graph by using an algorithm such as augmenting path algorithm or much faster and an improved algorithm known as Hopcroft-Karp bipartite matching algorithm. (Refer section 26-6)
? Repeat the process
¦ for all vertices which are not present in the maximum-matching set (set with largest number of edges), run BFS to find the augmenting path.
¦ Alternate unmatched/matched edges to select the edge which is in the maximum matching and are not connected from the vertices that are not a part maximum matching set.
¦ Reverse or flip the matched edges with unmatched edges and vice-versa.
? Stop the process if no augmenting path is found and return the last matching set.
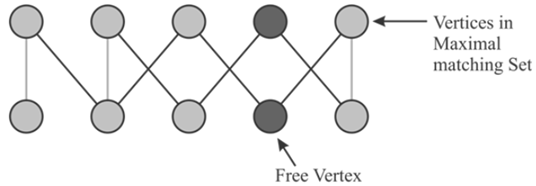
The running time or running complexity of the algorithm to solve the independent set problem is. The algorithm works correctly if there does not exist any augmenting path with respect to the maximal matching M as obtained by applying the bipartite matching algorithm.
Want to see more full solutions like this?
Chapter 34 Solutions
Introduction to Algorithms
- Please solve and answer the questions correctly please. Thank you!!arrow_forwardConsidering the TM example of binary sum ( see attached)do the step-by-step of execution for the binary numbers 1101 and 11. Feel free to use the Formal Language Editor Tool to execute it; Write it down the current state of the tape (including the head position) and indicate the current state of the TM at each step.arrow_forwardI need help on inculding additonal code where I can can do the opposite code of MatLab, where the function of t that I enter becomes the result of F(t), in other words, turning the time-domain f(t) into the frequency-domain function F(s):arrow_forward
 Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
Fundamentals of Information SystemsComputer ScienceISBN:9781305082168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning



