MyLab Math with Pearson eText -- 24-Month Standalone Access Card -- for Trigonometry
11th Edition
ISBN: 9780135909140
Author: Lial, Margaret, HORNSBY, John, SCHNEIDER, David, DANIELS, Callie
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.2, Problem 32E
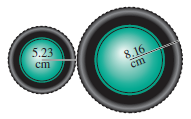
Rotating Wheels Repeat Exercise 31 for wheel radii of 6.84 in. and 12.46 in. and an
Rotating Wheels The rotation of the smaller wheel in the figure causes the larger wheel rotate. Through how many degrees does the larger wheel rotate if the smaller one rotates through 60.0°?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The second solution I got is incorrect.
What is the correct solution? The
other thrree with checkmarks are
correct
Question 19
Score on last try: 0.75 of 1 pts. See Details for more.
Get a similar question You can retry this question below
Solve 3 sin
2 for the four smallest positive solutions
0.75/1 pt 81 99 Details
T=
1.393,24.666,13.393,16.606
Give your answers accurate to at least two decimal places, as a list separated by commas
Question Help: Message instructor Post to forum
Submit Question
d₁ ≥ ≥ dn ≥ 0 with di even.
di≤k(k − 1) + + min{k, di}
vi=k+1
T2.5: Let d1, d2,...,d be integers such that n - 1
Prove the equivalence of the Erdos-Gallai conditions:
for each k = 1, 2, ………, n and the Edge-Count Criterion: Σier di + Σjeл(n − 1 − d;) ≥ |I||J| for
all I, JC [n] with In J = 0.
T2.4: Let d₁
Chapter 3 Solutions
MyLab Math with Pearson eText -- 24-Month Standalone Access Card -- for Trigonometry
Ch. 3.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 3.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 3.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 3.1 - CONCEPT PREVIEW Fill in the blank(s) to correctly...Ch. 3.1 - CONCEPT PREVIEW Each angle is an integer (e.g.,...Ch. 3.1 - CONCEPT PREVIEW Each angle is an integer (e.g.,...Ch. 3.1 - CONCEPT PREVIEW Each angle is an integer (e.g.,...Ch. 3.1 - CONCEPT PREVIEW Each angle is an integer (e.g.,...Ch. 3.1 - CONCEPT PREVIEW Each angle is an integer (e.g.,...Ch. 3.1 - CONCEPT PREVIEW Each angle is an integer (e.g.,...
Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 -
Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 - Prob. 20ECh. 3.1 -
Convert each degree measure to radians. Leave...Ch. 3.1 - Convert each degree measure to radians. Leave...Ch. 3.1 -
Convert each degree measure to radians. Leave...Ch. 3.1 - Prob. 24ECh. 3.1 -
Convert each degree measure to radians. Leave...Ch. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 -
Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 -
Convert each radian measure to degrees. See...Ch. 3.1 -
Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each radian measure to degrees. See...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Prob. 48ECh. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Prob. 52ECh. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Convert each degree measure to radians. If...Ch. 3.1 - Prob. 56ECh. 3.1 - Convert each radian measure to degrees. Write...Ch. 3.1 - Prob. 58ECh. 3.1 - Convert each radian measure to degrees. Write...Ch. 3.1 - Prob. 60ECh. 3.1 - Convert each radian measure to degrees. Write...Ch. 3.1 - Convert each radian measure to degrees. Write...Ch. 3.1 - Convert each radian measure to degrees. Write...Ch. 3.1 - Prob. 64ECh. 3.1 -
65. Concept Check The value of sin 30 is not ½....Ch. 3.1 - Prob. 66ECh. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 - Find each exact function value. See Example 3. secCh. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 -
Find each exact function value. See Example...Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 - Find each exact function value. See Example 3....Ch. 3.1 - Concept Check The figure shows the same angles...Ch. 3.1 - 88. Concept Check What is the exact radian measure...Ch. 3.1 - Prob. 89ECh. 3.1 - Concept Check Give an expression that generates...Ch. 3.1 - 91. Rotating Hour Hand on a Clock Through how many...Ch. 3.1 - 92. Rotating Minute Hand on a Clock Through how...Ch. 3.1 -
93. Orbits of a Space Vehicle A space vehicle is...Ch. 3.1 - Rotating Pulley A circular pulley is rotating...Ch. 3.1 -
95. Revolutions of a Carousel A stationary horse...Ch. 3.1 - 96. Railroad Engineering Some engineers use the...Ch. 3.2 -
CONCEPT PREVIEW Find the exact length of each...Ch. 3.2 - CONCEPT PREVIEW Find the exact length of each arc...Ch. 3.2 - CONCEPT PREVIEW Find the radius of each circle.Ch. 3.2 - CONCEPT PREVIEW Find the radius of each circle.Ch. 3.2 - CONCEPT PREVIEW Find the measure of each central...Ch. 3.2 - CONCEPT PREVIEW Find the measure of each central...Ch. 3.2 -
CONCEPT PREVIEW Find the area of each...Ch. 3.2 -
CONCEPT PREVIEW Find the area of each sector.
8....Ch. 3.2 -
CONCEPT PREVIEW Find the measure (in radians) of...Ch. 3.2 - CONCEPT PREVIEW Find the measure (in degrees) of...Ch. 3.2 -
CONCEPT PREVIEW Find the measure (in degrees) of...Ch. 3.2 - CONCEPT PREVIEW Find the measure (in degrees) of...Ch. 3.2 - Find the length to three significant digits of...Ch. 3.2 - Find the length to three significant digits of...Ch. 3.2 -
Find the length to three significant digits of...Ch. 3.2 - Find the length to three significant digits of...Ch. 3.2 -
Find the length to three significant digits of...Ch. 3.2 - Find the length to three significant digits of...Ch. 3.2 -
Find the length to three significant digits of...Ch. 3.2 - Find the length to three significant digits of...Ch. 3.2 - Concept Check If the radius of a circle is...Ch. 3.2 - Concept Check Radian measure simplifies many...Ch. 3.2 -
Distance between Cities Find the distance in...Ch. 3.2 -
Distance between Cities Find the distance in...Ch. 3.2 -
Distance between Cities Find the distance in...Ch. 3.2 -
Distance between Cities Find the distance in...Ch. 3.2 - Latitude of Madison Madison, South Dakota, and...Ch. 3.2 - Prob. 28ECh. 3.2 - Work each problem. See Examples 3 and 4. Gear...Ch. 3.2 - Gear Movement Repeat Exercise 29 for gear radii of...Ch. 3.2 - Rotating Wheels The rotation of the smaller wheel...Ch. 3.2 - Rotating Wheels Repeat Exercise 31 for wheel radii...Ch. 3.2 - Rotating Wheels Find the radius of the larger...Ch. 3.2 - Prob. 34ECh. 3.2 - Pulley Raising a Weight Refer to the figure. (a)...Ch. 3.2 -
36. Pulley Raising a Weight Find the radius of...Ch. 3.2 - Bicycle Chain Drive The figure shows the chain...Ch. 3.2 - Car Speedometer The speedometer of Terrys Honda...Ch. 3.2 -
Suppose the tip of the minute hand of a clock is...Ch. 3.2 -
Suppose the tip of the minute hand of a clock is...Ch. 3.2 -
Suppose the tip of the minute hand of a clock is...Ch. 3.2 - Suppose the tip of the minute hand of a clock is 3...Ch. 3.2 -
If a central angle is very small, there is little...Ch. 3.2 - 44. Repeat Exercise 43 for a railroad track 2.7 mi...Ch. 3.2 -
45. Distance to a Boat The mast of a boat is 32.0...Ch. 3.2 - Repeat Exercise 45 for a boat mast 11.0m high the...Ch. 3.2 -
Find the area of a sector of a circle having...Ch. 3.2 - Find the area of a sector of a circle having...Ch. 3.2 - Find the area of a sector of a circle having...Ch. 3.2 - Prob. 50ECh. 3.2 -
Find the area of a sector of a circle having...Ch. 3.2 -
Find the area of a sector of a circle having...Ch. 3.2 - Find the area of a sector of a circle having...Ch. 3.2 -
Find the area of a sector of a circle having...Ch. 3.2 - Angle Measure Find the measure (in radians) of a...Ch. 3.2 -
56. Radius Length Find the radius of a circle in...Ch. 3.2 -
57. Irrigation Area A center-pivot irrigation...Ch. 3.2 - Irrigation Area Suppose that in Exercise 57 the...Ch. 3.2 -
59. Arc Length A circular sector has an area of...Ch. 3.2 -
60. Angle Measure In a circle, a sector has an...Ch. 3.2 -
61. Measures of a Structure The figure...Ch. 3.2 - Area Cleaned by a Windshield Wiper The Ford Model...Ch. 3.2 -
63. Circular Railroad Curves In the United...Ch. 3.2 - Land Required for a Solar-Power Plant A...Ch. 3.2 -
65. Area of a Lot A frequent problem in surveying...Ch. 3.2 - Nautical Miles Nautical miles are used by ships...Ch. 3.2 - Prob. 67ECh. 3.2 -
68. Longitude Longitude is the angular distance...Ch. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.3 -
CONCEPT PREVIEW Fill in the blanks to complete...Ch. 3.3 - Prob. 2ECh. 3.3 - CONCEPT PREVIEW Fill in the blanks to complete the...Ch. 3.3 - Prob. 4ECh. 3.3 -
CONCEPT PREVIEW Fill in the blanks to complete...Ch. 3.3 - Prob. 6ECh. 3.3 -
CONCEPT PREVIEW Each figure shows an angle θ in...Ch. 3.3 -
CONCEPT PREVIEW Each figure shows an angle θ in...Ch. 3.3 - CONCEPT PREVIEW Each figure shows an angle in...Ch. 3.3 - Prob. 10ECh. 3.3 -
Find the exact values of (a) sin s, (b) cos s,...Ch. 3.3 -
Find the exact values of (a) sin s, (b) cos s,...Ch. 3.3 - Find the exact values of (a) sin s, (b) cos s, and...Ch. 3.3 - Prob. 14ECh. 3.3 - Find the exact values of (a) sin s, (b) cos s, and...Ch. 3.3 -
Find the exact values of (a) sin s, (b) cos s,...Ch. 3.3 - Find each exact function value. See Example 2.
17....Ch. 3.3 - Find each exact function value. See Example 2. cos...Ch. 3.3 - Find each exact function value. See Example 2.
19....Ch. 3.3 - Find each exact function value. See Example 2.
20....Ch. 3.3 - Find each exact function value. See Example 2. csc...Ch. 3.3 - Find each exact function value. See Example 2. cot...Ch. 3.3 - Find each exact function value. See Example 2. cos...Ch. 3.3 -
Find each exact function value. See Example...Ch. 3.3 -
Find each exact function value. See Example...Ch. 3.3 -
Find each exact function value. See Example...Ch. 3.3 - Find each exact function value. See Example 2. sin...Ch. 3.3 - Find each exact function value. See Example 2. sin...Ch. 3.3 -
Find each exact function value. See Example...Ch. 3.3 - Find each exact function value. See Example 2. csc...Ch. 3.3 - Find each exact function value. See Example 2. tan...Ch. 3.3 - Prob. 32ECh. 3.3 - Find a calculator approximation to four decimal...Ch. 3.3 - Prob. 34ECh. 3.3 -
Find a calculator approximation to four decimal...Ch. 3.3 - Prob. 36ECh. 3.3 -
Find a calculator approximation to four decimal...Ch. 3.3 - Prob. 38ECh. 3.3 -
Find a calculator approximation to four decimal...Ch. 3.3 -
Find a calculator approximation to four decimal...Ch. 3.3 - Find a calculator approximation to four decimal...Ch. 3.3 -
Find a calculator approximation to four decimal...Ch. 3.3 - Find a calculator approximation to four decimal...Ch. 3.3 - Prob. 44ECh. 3.3 - Concept Check The figure displays a unit circle...Ch. 3.3 - Prob. 46ECh. 3.3 - Concept Check The figure displays a unit circle...Ch. 3.3 - Concept Check The figure displays a unit circle...Ch. 3.3 - Concept Check The figure displays a unit circle...Ch. 3.3 - Prob. 50ECh. 3.3 -
Concept Check The figure displays a unit circle...Ch. 3.3 - Concept Check The figure displays a unit circle...Ch. 3.3 -
Concept Check The figure displays a unit circle...Ch. 3.3 - Concept Check The figure displays a unit circle...Ch. 3.3 - Concept Check Without using a calculator, decide...Ch. 3.3 - Concept Check Without using a calculator, decide...Ch. 3.3 - Concept Check Without using a calculator, decide...Ch. 3.3 -
Concept Check Without using a calculator, decide...Ch. 3.3 - Prob. 59ECh. 3.3 - Concept Check Without using a calculator, decide...Ch. 3.3 -
Find the approximate value of s, to four decimal...Ch. 3.3 - Find the approximate value of s, to four decimal...Ch. 3.3 - Find the approximate value of s, to four decimal...Ch. 3.3 -
Find the approximate value of s, to four decimal...Ch. 3.3 - Find the approximate value of s, to four decimal...Ch. 3.3 -
Find the approximate value of s, to four decimal...Ch. 3.3 - Find the exact value of s in the given interval...Ch. 3.3 -
Find the exact value of s in the given interval...Ch. 3.3 - Find the exact value of s in the given interval...Ch. 3.3 -
Find the exact value of s in the given interval...Ch. 3.3 -
Find the exact value of s in the given interval...Ch. 3.3 -
Find the exact value of s in the given interval...Ch. 3.3 - Find the exact values of s in the given interval...Ch. 3.3 - Find the exact values of s in the given interval...Ch. 3.3 - Find the exact values of s in the given interval...Ch. 3.3 - Find the exact values of s in the given interval...Ch. 3.3 -
Find the exact values of s in the given interval...Ch. 3.3 - Find the exact values of s in the given interval...Ch. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Prob. 81ECh. 3.3 - Prob. 82ECh. 3.3 -
Concept Check For each value of s, use a...Ch. 3.3 - Prob. 84ECh. 3.3 -
Concept Check For each value of s, use a...Ch. 3.3 - Prob. 86ECh. 3.3 - Prob. 87ECh. 3.3 - Prob. 88ECh. 3.3 -
(Modeling) Solve each problem See Example 5.
89....Ch. 3.3 - Length of a Day The number of daylight hours H at...Ch. 3.3 - Maximum Temperatures Because the values of the...Ch. 3.3 - Temperature in Fairbanks Suppose the temperature...Ch. 3.3 - Prob. 93ECh. 3.3 - Prob. 94ECh. 3.3 - Prob. 1QCh. 3.3 - Convert each degree measure to radians.
2. –330°
Ch. 3.3 - Prob. 3QCh. 3.3 - Prob. 4QCh. 3.3 - Prob. 5QCh. 3.3 - A central angle of a circle with radius 300 in....Ch. 3.3 - Prob. 7QCh. 3.3 - Find each exact circular function value. sin -56Ch. 3.3 -
Find each exact circular function value.
9. tan...Ch. 3.3 - Prob. 10QCh. 3.4 - CONCEPT PREVIEW Fill in the blank to correctly...Ch. 3.4 - CONCEPT PREVIEW Fill in the blank to correctly...Ch. 3.4 -
CONCEPT PREVIEW Fill in the blank to correctly...Ch. 3.4 - CONCEPT PREVIEW Fill in the blank to correctly...Ch. 3.4 -
CONCEPT PREVIEW Fill in the blank to correctly...Ch. 3.4 -
CONCEPT PREVIEW Fill in the blank to correctly...Ch. 3.4 - Suppose that point P is on a circle with radius r,...Ch. 3.4 - Suppose that point P is on a circle with radius r,...Ch. 3.4 - Suppose that point P is on a circle with radius r,...Ch. 3.4 -
Suppose that point P is on a circle with radius...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula ω = to find the value of the...Ch. 3.4 -
Use the formula ω = to find the value of the...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula ω = to find the value of the...Ch. 3.4 - Use the formula = t to find the value of the...Ch. 3.4 - Use the formula v = r to find the value of the...Ch. 3.4 - Use the formula v = rω to find the value of the...Ch. 3.4 - Use the formula v = rω to find the value of the...Ch. 3.4 - Use the formula v = rω to find the value of the...Ch. 3.4 - Use the formula v = rω to find the value of the...Ch. 3.4 - Use the formula v = r to find the value of the...Ch. 3.4 - The formula =t can be rewritten as = t....Ch. 3.4 - The formula =t can be rewritten as = t....Ch. 3.4 - The formula can be rewritten as θ = ωt....Ch. 3.4 - The formula can be rewritten as θ = ωt....Ch. 3.4 -
The formula can be rewritten as θ = ωt....Ch. 3.4 - Prob. 32ECh. 3.4 - Find the angular speed for each of the following....Ch. 3.4 - Find the angular speed for each of the following....Ch. 3.4 - Find the angular speed for each of the following....Ch. 3.4 - Find the angular speed for each of the following....Ch. 3.4 -
Find the linear speed v for each of the...Ch. 3.4 -
Find the linear speed v for each of the...Ch. 3.4 - Find the linear speed v for each of the following....Ch. 3.4 - Find the linear speed v for each of the following....Ch. 3.4 -
Find the linear speed v for each of the...Ch. 3.4 -
Find the linear speed v for each of the...Ch. 3.4 - Speed of a Bicycle The tires of a bicycle have...Ch. 3.4 - Hours in a Martian Day Mars rotates on its axis at...Ch. 3.4 - Angular and Linear Speeds of Earth The orbit of...Ch. 3.4 -
46. Angular and Linear Speeds of Earth Earth...Ch. 3.4 - Speeds of a Pulley and a Belt The pulley shown has...Ch. 3.4 - Angular Speeds of Pulleys The two pulleys in the...Ch. 3.4 - Radius of a Spool of Thread A thread is being...Ch. 3.4 - Prob. 50ECh. 3.4 -
51. Angular Speed of a Motor Propeller The...Ch. 3.4 - Linear Speed of a Golf Club The shoulder joint can...Ch. 3 - 1. What is the meaning of “an angle with measure 2...Ch. 3 - Consider each angle in standard position having...Ch. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Convert each degree measure to radians. Leave...Ch. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Convert each degree measure to radians. Leave...Ch. 3 - Convert each radian measure to degrees. 54Ch. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - Prob. 14RECh. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 -
21. Arc Length The radius of a circle is 15.2...Ch. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - 24. Angle Measure Find the measure (in radians) of...Ch. 3 - Area of a Sector Find the area of a sector of a...Ch. 3 - Area of a Sector A central angle of 74 radians...Ch. 3 - Diameter of the Moon The distance to the moon is...Ch. 3 - 28. Concept Check Using s = r θ and A = , express...Ch. 3 - Prob. 29RECh. 3 - 30. Concept Check What would happen to the central...Ch. 3 - Distance between Cities Assume that the radius of...Ch. 3 - 32. Two cities on the equator have longitudes of...Ch. 3 - Prob. 33RECh. 3 - Concept Check Find the measure of each central...Ch. 3 - Find each exact function value. tan3Ch. 3 -
Find each exact function value.
36.
Ch. 3 - Prob. 37RECh. 3 - Find each exact function value. tan(73)Ch. 3 - Find each exact function value. csc(116)Ch. 3 - Find each exact function value. cot(13)Ch. 3 - Prob. 41RECh. 3 -
Concept Check Without using a calculator,...Ch. 3 - Concept Check Without using a calculator,...Ch. 3 - Concept Check Match each domain in Column II with...Ch. 3 - Find a calculator approximation to four decimal...Ch. 3 - Find a calculator approximation to four decimal...Ch. 3 - Prob. 47RECh. 3 - Find a calculator approximation to four decimal...Ch. 3 - Find a calculator approximation to four decimal...Ch. 3 - Find a calculator approximation to four decimal...Ch. 3 - Find the approximate value of s, to four decimal...Ch. 3 - Find the approximate value of s, to four decimal...Ch. 3 - Prob. 53RECh. 3 - Find the approximate value of s. to four decimal...Ch. 3 - Find the approximate value of s, to four decimal...Ch. 3 - Find the approximate value of s, to four decimal...Ch. 3 - Prob. 57RECh. 3 - Find the exact value of s in the given interval...Ch. 3 - Find the exact value of s in the given interval...Ch. 3 - Find the exact value of s in the given interval...Ch. 3 -
Suppose that point P is on a circle with radius...Ch. 3 -
Suppose that point P is on a circle with radius...Ch. 3 - 63. Linear Speed of a Flywheel Find the linear...Ch. 3 - Angular Speed of a Ferris Wheel A Ferris wheel has...Ch. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - Convert each degree measure to radians. 1200Ch. 3 - Convert each degree measure to radians. - 450Ch. 3 -
Convert each degree measure to radians.
3. 5° (to...Ch. 3 - Convert each radian measure to degrees. 34Ch. 3 -
Convert each radian measure to degrees.
5.
Ch. 3 -
Convert each radian measure to degrees.
6. 4(to...Ch. 3 - 7. A central angle of a circle with radius 150 cm...Ch. 3 -
8. Rotation of Gas Gauge Arrow The arrow on a...Ch. 3 -
Find each exact function value.
9.
Ch. 3 - Prob. 10TCh. 3 - Prob. 11TCh. 3 - Prob. 12TCh. 3 - Prob. 13TCh. 3 - Prob. 14TCh. 3 -
15. Determine the six exact circular function...Ch. 3 -
16. Give the domains of the six circular...Ch. 3 -
17. (a) Use a calculator to approximate s in the...Ch. 3 - Prob. 18TCh. 3 - Orbital Speed of Jupiter It takes Jupiter 11.86 yr...Ch. 3 - Ferris Wheel A Ferris wheel has radius 50.0 ft. A...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, trigonometry and related others by exploring similar questions and additional content below.Similar questions
- T2.3: Prove that there exists a connected graph with degrees d₁ ≥ d₂ >> dn if and only if d1, d2,..., dn is graphic, d ≥ 1 and di≥2n2. That is, some graph having degree sequence with these conditions is connected. Hint - Do not attempt to directly prove this using Erdos-Gallai conditions. Instead work with a realization and show that 2-switches can be used to make a connected graph with the same degree sequence. Facts that can be useful: a component (i.e., connected) with n₁ vertices and at least n₁ edges has a cycle. Note also that a 2-switch using edges from different components of a forest will not necessarily reduce the number of components. Make sure that you justify that your proof has a 2-switch that does decrease the number of components.arrow_forwardT2.2 Prove that a sequence s d₁, d₂,..., dn with n ≥ 3 of integers with 1≤d; ≤ n − 1 is the degree sequence of a connected unicyclic graph (i.e., with exactly one cycle) of order n if and only if at most n-3 terms of s are 1 and Σ di = 2n. (i) Prove it by induction along the lines of the inductive proof for trees. There will be a special case to handle when no d₂ = 1. (ii) Prove it by making use of the caterpillar construction. You may use the fact that adding an edge between 2 non-adjacent vertices of a tree creates a unicylic graph.arrow_forward= == T2.1: Prove that the necessary conditions for a degree sequence of a tree are sufficient by showing that if di 2n-2 there is a caterpillar with these degrees. Start the construction as follows: if d1, d2,...,d2 and d++1 = d = 1 construct a path v1, v2, ..., vt and add d; - 2 pendent edges to v, for j = 2,3,..., t₁, d₁ - 1 to v₁ and d₁ - 1 to v₁. Show that this construction results vj in a caterpillar with degrees d1, d2, ..., dnarrow_forward
- 4 sin 15° cos 15° √2 cos 405°arrow_forward2 18-17-16-15-14-13-12-11-10 -9 -8 -6 -5 -4-3-2-1 $ 6 8 9 10 -2+ The curve above is the graph of a sinusoidal function. It goes through the points (-10, -1) and (4, -1). Find a sinusoidal function that matches the given graph. If needed, you can enter π-3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Questionarrow_forwardketch a graph of the function f(x) = 3 cos (표) 6. x +1 5 4 3 3 80 9 2+ 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3+ -4 5 -6+ Clear All Draw: пи > Next Questionarrow_forward
- Draw the following graph on the interval πT 5π < x < 2 2 y = 2 sin (2(x+7)) 6. 5. 4 3 3 2 1 +3 /2 -π/3 -π/6 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/311π/6 2π 13π/67π/3 5π Clear All Draw:arrow_forwardketch a graph of the function f(x) = 3 cos (표) 6. x +1 5 4 3 3 80 9 2+ 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 -3+ -4 5 -6+ Clear All Draw: пи > Next Questionarrow_forward3 2 20-10-18-17-16-15-14-13-12-11-10-9 -8 -7 -6 -$4-3-2-1 -1 -2 -3 4- -5+ The curve above is the graph of a sinusoidal function. It goes through the points (-8, -4) and (6,-4). Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Question Barrow_forward
- X Grades for X Assignmen X A-Z Datab XE Biocultural X EBSCO-Ful X Review es/119676/assignments/3681238 Review Quiz 8.1-p2 points possible Answered: 3/5 ● Question 1 4+ 3. 2 1 13 /12-11 -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 -1 -2 -3 -4- 5 2 6 The curve above is the graph of a sinusoidal function. It goes through the points (-7,0) and (3,0). Find a sinusoidal function that matches the given graph. If needed, you can enter π=3.1416... as 'pi' in your answer, otherwise use at least 3 decimal digits. f(x) = > Next Question 申 J % F 刀 Q Search S € t ח Y 7 I * 00 J ப I Darrow_forward2 d) Draw the following graph on the interval k 5π Next Questionarrow_forwardDraw the following graph on the interval 5л Next Questionarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Problems on Area and Circumference of Circle| Basics of Circle| Questions on Circle||BrainPanthers; Author: Brain Panthers;https://www.youtube.com/watch?v=RcNEL9OzcC0;License: Standard YouTube License, CC-BY