The Gateway Arch in St. Louis was designed by Eero Saarinen and was constructed using the equation y = 211.49 − 20.96 cosh(0.03291765x) for the central curve of the arch, where x and y are in meters and |x| ≤ 91.20. a-What is the height (in m) of the arch at its center? (Round your answer to two decimal places.) b-At what points is the height 50 m? (Round your answers to two decimal places.) smaller x-value (x, y)= larger x-value (x, y)= c-What is the slope of the arch at the points in part b? (Round your answers to one decimal place.)
The Gateway Arch in St. Louis was designed by Eero Saarinen and was constructed using the equation y = 211.49 − 20.96 cosh(0.03291765x) for the central curve of the arch, where x and y are in meters and |x| ≤ 91.20. a-What is the height (in m) of the arch at its center? (Round your answer to two decimal places.) b-At what points is the height 50 m? (Round your answers to two decimal places.) smaller x-value (x, y)= larger x-value (x, y)= c-What is the slope of the arch at the points in part b? (Round your answers to one decimal place.)
Advanced Engineering Mathematics
10th Edition
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Erwin Kreyszig
Chapter2: Second-order Linear Odes
Section: Chapter Questions
Problem 1RQ
Related questions
Question
A graphing calculator is recommended.
The Gateway Arch in St. Louis was designed by Eero Saarinen and was constructed using the equation
y = 211.49 − 20.96 cosh(0.03291765x)
for the central curve of the arch, where x and y are in meters and
|x| ≤ 91.20.
a-What is the height (in m) of the arch at its center? (Round your answer to two decimal places.)
b-At what points is the height 50 m? (Round your answers to two decimal places.)
smaller x-value (x, y)=
larger x-value (x, y)=
larger x-value (x, y)=
c-What is the slope of the arch at the points in part b? (Round your answers to one decimal place.)
| at the point with smaller x-value | |
| at the point with larger x-value |
Expert Solution
Step 1
Step:-1
Given equation is and x, y are in meters and
Sketching the graph using given equation, we get
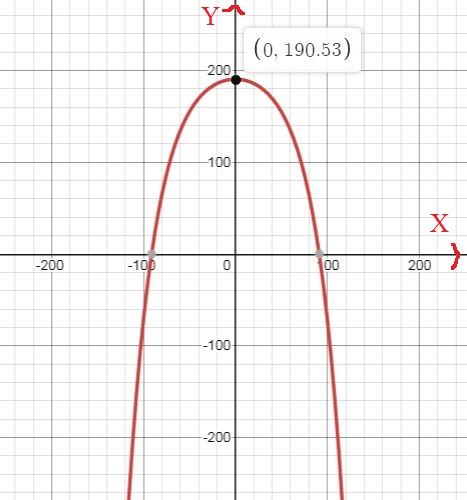
This is parabola opens downward.
Part (a):-
The height of arch at its center is
So, height is 190.63 meter.
or
Using graph, we can see the height of arch is 190.53 meter.
Answer:-
height = 190.63 meter.
Step:-2
Part (b):-
Given that height is 50 m.
Now, we have to find the value of x for which arch attains height 50 m.
Given equation is
Step:-3
by (1), we get
Step:-4
Applying quadratic formula, we get
Answer:-
Smaller x-value
Larger x-value
Trending now
This is a popular solution!
Step by step
Solved in 2 steps with 1 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Recommended textbooks for you

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Advanced Engineering Mathematics
Advanced Math
ISBN:
9780470458365
Author:
Erwin Kreyszig
Publisher:
Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:
9780073397924
Author:
Steven C. Chapra Dr., Raymond P. Canale
Publisher:
McGraw-Hill Education

Introductory Mathematics for Engineering Applicat…
Advanced Math
ISBN:
9781118141809
Author:
Nathan Klingbeil
Publisher:
WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:
9781337798310
Author:
Peterson, John.
Publisher:
Cengage Learning,

