Problem 1FT: True or False? Explain. The domain and range of a quadratic function are (– ∞ , ∞ ). Problem 2FT: True or False? Explain. The vertex of the graph of y = 2(x –3)2 –1 is (3, 1). Problem 3FT Problem 4FT Problem 5FT: True or False? Explain. For y = 3x2 –6x + 7, the value of y is at its minimum when x = 1. Problem 6FT Problem 7FT Problem 8FT Problem 9FT: True or False? Explain.
9. The maximum area of a rectangle with fixed perimeter p is p2/16.
Problem 10FT Problem 1E: If a > 0, the graph of f(x) = a(x – h)2 + k opens _______. Problem 2E: Fill in the blank.
2. If a < 0, the graph of f(x) = a(x – h)2 + k opens ______.
Problem 3E: Fill in the blank. The point (h, k) is the _______ of the parabola y = a(x– h)2 + k. Problem 4E: Fill in the blank. For f ( x ) = a x 2 + b x + c ( a ≠ 0 ) , the x-coordinate of the ______... Problem 5E: Fill in the blank.
5. If a > 0 and f(x) = a(x – h)2 + k, then k is the ______ value of the... Problem 6E: Fill in the blank. If a< 0 and f(x) = a(x – h)2 + k, then k is the ______ value of the function. Problem 7E: Fil in the blank.
7. The line x =–b/(2a) is the _________ for the function .
Problem 8E: Fill in the blank.
8. The point (0, c) is the _________ for the function .
Problem 9E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = x2 + 4x Problem 10E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = x2 –6x Problem 11E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = x2 –3x Problem 12E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = x2 +5x Problem 13E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = 2x2 –12x + 22 Problem 14E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = 3x2 – 12x + 1 Problem 15E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = –3x2 +6x –3 Problem 16E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph.
16. y = –2x2 –4x +... Problem 17E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph.
17.
Problem 18E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph.
18. y = x2 – x +... Problem 19E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph.
19. y = –2x2 + 3x... Problem 20E: Write each quadratic function in the form y = a(x – h)2 + k and sketch its graph. y = 3x2 +4x + 2 Problem 21E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 22E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 23E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 24E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 25E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 26E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 27E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 28E: Find the vertex of the graph of each quadratic function. See the summary on finding the vertex on... Problem 29E: From the graph of each parabola, determine whether the parabola opens upward or downward, and find... Problem 30E: From the graph of each parabola, determine whether the parabola opens upward or downward, and find... Problem 31E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 32E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 33E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 34E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 35E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 36E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 37E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 38E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 39E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 40E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 41E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 42E: Find the range of each quadratic function and the maximum or minimum value of the function. Identify... Problem 43E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 44E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, opening of each parabola, then... Problem 45E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, opening of each parabola, then... Problem 46E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, opening of each parabola, then... Problem 47E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 48E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 49E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, opening of each parabola, then... Problem 50E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 51E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, opening of each parabola, then... Problem 52E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 53E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 54E: Identify the vertex, axis of symmetry, y-intercept, x-intercepts, and opening of each parabola, then... Problem 55E: Solve each inequality by using the graphical method. State the solution set in interval... Problem 56E: Solve each inequality by using the graphical method. State the solution set in interval notation. x2... Problem 57E: Solve each inequality by using the graphical method. State the solution set in interval notation. x2... Problem 58E: Solve each inequality by using the graphical method. State the solution set in interval notation. x2... Problem 59E: Solve each inequality by using the graphical method. State the solution set in interval... Problem 60E: Solve each inequality by using the graphical method. State the solution set in interval notation. x... Problem 61E: Identify the solution set to each quadratic inequality by inspecting the graphs of y = x2 –2x –3 and... Problem 62E: Identify the solution set to each quadratic inequality by inspecting the graphs of y = x2 –2x –3 and... Problem 63E: Identify the solution set to each quadratic inequality by inspecting the graphs of y = x2 –2x – 3... Problem 64E: Identify the solution set to each quadratic inequality by inspecting the graphs of y = x2 –2x –3 and... Problem 65E: Identify the solution set to each quadratic inequality by inspecting the graphs of y = x2 –2x –3 and... Problem 66E: Identify the solution set to each quadratic inequality by inspecting the graphs of y = x2 –2x –3 and... Problem 67E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 68E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 69E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 70E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 71E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 72E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 73E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 74E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 75E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 76E Problem 77E Problem 78E Problem 79E Problem 80E Problem 81E Problem 82E Problem 83E: Solve each inequality by using the test-point method. State the solution set in interval notation... Problem 84E: Solve each inequality by using the method of your choice. State the solution set in interval... Problem 85E: Solve each inequality by using the method of your choice. State the solution set in interval... Problem 86E: Solve each inequality by using the method of your choice. State the solution set in interval... Problem 87E: Solve each inequality by using the method of your choice. State the solution set in interval... Problem 88E: Solve each inequality by using the method of your choice. State the solution set in interval... Problem 89E Problem 90E Problem 91E Problem 92E Problem 93E: Solve each problem.
93. Maximum Height of a Football If a football is kicked straight up with an... Problem 94E Problem 95E: Solve each problem. Shooting an Arrow If an archer shoots an arrow straight upward with an initial... Problem 96E Problem 97E Problem 98E: The next two exercises incorporate many concepts of quadratics. Average Farm Size The average size... Problem 99E Problem 100E: The next two exercises incorporate many concepts of quadratics. Mirror Mirror Chantel wants to make... Problem 101E: The next two exercises incorporate many concepts of quadratics. Twin Kennels Martin plans to... Problem 102E Problem 103E: The next two exercises incorporate many concepts of quadratics. Big Barn Mike wants to enclose a... Problem 104E Problem 105E: The next two exercises incorporate many concepts of quadratics.
105. Cross Section of a Gutter Seth... Problem 106E: The next two exercises incorporate many concepts of quadratics. Maximum Volume of a Cage Sharon has... Problem 107E Problem 108E: The next two exercises incorporate many concepts of quadratics.
108. Concert Tickets At $10 per... Problem 109E: The next two exercises incorporate many concepts of quadratics. Variance of the Number of Smokers If... Problem 110E Problem 111E Problem 112E Problem 113E: Use a calculator or a computer for the following regression problems.
113. Quadratic Versus Linear... Problem 114E Problem 115E Problem 116E Problem 117E Problem 118E Problem 119E Problem 120E Problem 121E Problem 122E: Use a calculator or a computer for the following regression problems. Integral Pairs Find all... Problem 1PQ Problem 2PQ Problem 3PQ Problem 4PQ Problem 5PQ Problem 6PQ Problem LC: LINKING
concepts...
For Individual or Group Explorations
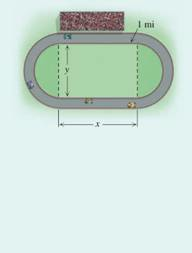
Designing a Race Track
An architect is... format_list_bulleted

 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
 Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill




