COLLEGE ALGEBRA
COLLEGE ALGEBRA
2nd Edition
ISBN: 9781260618907
Author: Miller
Publisher: MCG
bartleby

Videos

Textbook Question
Book Icon
Chapter 3.1, Problem 77PE

For Exercises 71–78, given a quadratic function defined by f ( x ) = a ( x − h ) 2 + k ( a ≠ 0 ) , match the graph with the function based on the conditions given.

Chapter 3.1, Problem 77PE, For Exercises 71–78, given a quadratic function defined by, match the graph with the function based , example 1

Chapter 3.1, Problem 77PE, For Exercises 71–78, given a quadratic function defined by, match the graph with the function based , example 2

a < 0 , h = 2 , axis of symmetry x = 2 , k < 0

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 3.1, Problem 76PE
Next
Chapter 3.1, Problem 78PE
Students have asked these similar questions
Solve the system of equation for y using Cramer's rule. Hint: The determinant of the coefficient matrix is -23. - 5x + y − z = −7 2x-y-2z = 6 3x+2z-7
eric pez Xte in z= Therefore, we have (x, y, z)=(3.0000, 83.6.1 Exercise Gauss-Seidel iteration with Start with (x, y, z) = (0, 0, 0). Use the convergent Jacobi i Tol=10 to solve the following systems: 1. 5x-y+z = 10 2x-8y-z=11 -x+y+4z=3 iteration (x Assi 2 Assi 3. 4. x-5y-z=-8 4x-y- z=13 2x - y-6z=-2 4x y + z = 7 4x-8y + z = -21 -2x+ y +5z = 15 4x + y - z=13 2x - y-6z=-2 x-5y- z=-8 realme Shot on realme C30 2025.01.31 22:35 f
Use Pascal's triangle to expand the binomial  (6m+2)^2

Chapter 3 Solutions

COLLEGE ALGEBRA

Ch. 3.1 - Skill Practice 1 Repeat Example 1 with Ch. 3.1 - Skill Practice 2 Repeat Example 2 with...Ch. 3.1 - Skill Practice 3 Repeat Example 3 with f(x)=x24x7.Ch. 3.1 - Skill Practice 4 A quarterback throws a football...Ch. 3.1 - Skill Practice 5 A farmer has 200 ft of fencing...Ch. 3.1 - Skill Practice 6 The funding f(t) (in $ millions)...Ch. 3.1 - 1. A function defined by is called a...Ch. 3.1 - Prob. 2PECh. 3.1 - Prob. 3PECh. 3.1 - Prob. 4PE
Ch. 3.1 - 5. Given if, the parabola opens (upward/downward)...Ch. 3.1 - Prob. 6PECh. 3.1 - For Exercises 7–14, a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - For Exercises 7–14, a. Determine whether the graph...Ch. 3.1 - For Exercises 7–14, a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - For Exercises 714, a. Determine whether the graph...Ch. 3.1 - Prob. 14PECh. 3.1 - For Exercises 15–24, a. Write the function in...Ch. 3.1 - Prob. 16PECh. 3.1 - For Exercises 15–24, a. Write the function in...Ch. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - For Exercises 15–24, a. Write the function in...Ch. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - Prob. 22PECh. 3.1 - For Exercises 1524, a. Write the function in...Ch. 3.1 - Prob. 24PECh. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - Prob. 26PECh. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - For Exercises 25–32, find the vertex of the...Ch. 3.1 - For Exercises 25–32, find the vertex of the...Ch. 3.1 - For Exercises 25–32, find the vertex of the...Ch. 3.1 - For Exercises 2532, find the vertex of the...Ch. 3.1 - For Exercises 33–42, a. State whether the graph of...Ch. 3.1 - For Exercises 33–42, a. State whether the graph of...Ch. 3.1 - For Exercises 33–42, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 33–42, a. State whether the graph of...Ch. 3.1 - For Exercises 33–42, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - For Exercises 3342, a. State whether the graph of...Ch. 3.1 - 43. The monthly profit for a small company that...Ch. 3.1 - 44. The monthly profit for a company that makes...Ch. 3.1 - A long jumper leaves the ground at an angle of 208...Ch. 3.1 - 46. A firefighter holds a hose 3 m off the ground...Ch. 3.1 - 47. The population of a culture of the bacterium...Ch. 3.1 - 48. The gas mileage m(x) (in mpg) for a certain...Ch. 3.1 - 49. The sum of two positive numbers is 24. What...Ch. 3.1 - Prob. 50PECh. 3.1 - Prob. 51PECh. 3.1 - Prob. 52PECh. 3.1 - Suppose that a family wants to fence in an area of...Ch. 3.1 - 54. Two chicken coops are to be built adjacent to...Ch. 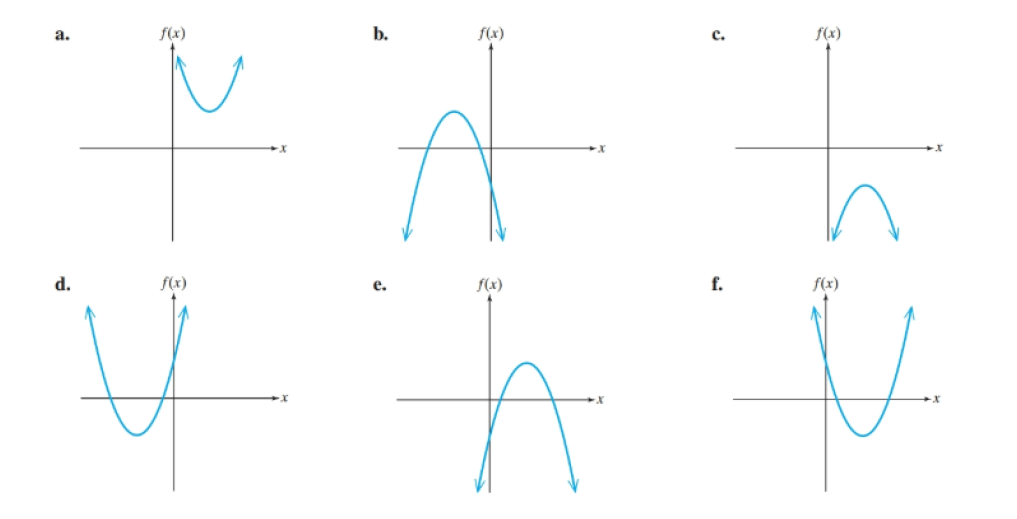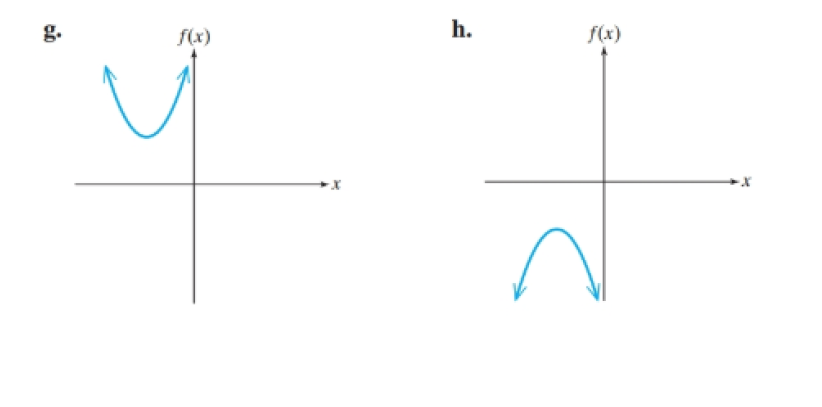3.1 - 55. A trough at the end of a gutter spout is meant...Ch. 3.1 - A rectangular frame of uniform depth for a shadow...Ch. 3.1 - Prob. 57PECh. 3.1 - Gas mileage is tested for a car under different...Ch. 3.1 - 59. Fluid runs through a drainage pipe with a...Ch. 3.1 - The braking distance required for a car to stop...Ch. 3.1 - Prob. 61PECh. 3.1 - For Exercises 6164, given a quadratic function...Ch. 3.1 - Prob. 63PECh. 3.1 - For Exercises 61–64, given a quadratic function...Ch. 3.1 - Prob. 65PECh. 3.1 - Prob. 66PECh. 3.1 - Prob. 67PECh. 3.1 - Prob. 68PECh. 3.1 - Prob. 69PECh. 3.1 - Prob. 70PECh. 3.1 - Prob. 71PECh. 3.1 - For Exercises 71–78, given a quadratic function...Ch. 3.1 - Prob. 73PECh. 3.1 - For Exercises 7178, given a quadratic function...Ch. 3.1 - Prob. 75PECh. 3.1 - Prob. 76PECh. 3.1 - For Exercises 71–78, given a quadratic function...Ch. 3.1 - For Exercises 7178, given a quadratic function...Ch. 3.1 - Prob. 79PECh. 3.1 - Prob. 80PECh. 3.1 - Prob. 81PECh. 3.1 - Prob. 82PECh. 3.1 - Prob. 83PECh. 3.1 - Prob. 84PECh. 3.1 - Prob. 85PECh. 3.1 - Prob. 86PECh. 3.1 - Prob. 87PECh. 3.1 - For Exercises 85 88, define a quadratic function...Ch. 3.1 - Prob. 89PECh. 3.1 - Prob. 90PECh. 3.1 - Prob. 91PECh. 3.1 - Prob. 92PECh. 3.2 - Skill Practice 1 Use the leading term to...Ch. 3.2 - Skill Practice 2 Find the zeros of the function...Ch. 3.2 - Skill Practice 3 Find the zeros of the function...Ch. 3.2 - Skill Practice 4 Use the leading term to determine...Ch. 3.2 - Skill Practice 5 Show that f(x)=x4+6x326x+15 has a...Ch. 3.2 - Skill Practice 6 Graph . Ch. 3.2 - Skill Practice 7 Graph h(x)=05x(x1)(x+3)2.Ch. 3.2 - 1. A function defined by where are real...Ch. 3.2 - Prob. 2PECh. 3.2 - Prob. 3PECh. 3.2 - Prob. 4PECh. 3.2 - Prob. 5PECh. 3.2 - Prob. 6PECh. 3.2 - Prob. 7PECh. 3.2 - Prob. 8PECh. 3.2 - Prob. 9PECh. 3.2 - Prob. 10PECh. 3.2 - Prob. 11PECh. 3.2 - Prob. 12PECh. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - For Exercises 13–20, determine the end behavior of...Ch. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - Prob. 16PECh. 3.2 - For Exercises 13–20, determine the end behavior of...Ch. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - For Exercises 1320, determine the end behavior of...Ch. 3.2 - For Exercises 13–20, determine the end behavior of...Ch. 3.2 - Given the function defined by g(x)=3(x1)3(x+5)4,...Ch. 3.2 - Given the function defined by h(x)=12x5(x+0.6)3,...Ch. 3.2 - For Exercises 2338, find the zeros of the function...Ch. 3.2 - For Exercises 2338, find the zeros of the function...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 2338, find the zeros of the function...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - Prob. 34PECh. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 23–38, find the zeros of the...Ch. 3.2 - For Exercises 39–40, determine whether the...Ch. 3.2 - For Exercises 39–40, determine whether the...Ch. 3.2 - Prob. 41PECh. 3.2 - Prob. 42PECh. 3.2 - Prob. 43PECh. 3.2 - Prob. 44PECh. 3.2 - For Exercises 4552, determine if the graph can...Ch. 3.2 - Prob. 46PECh. 3.2 - For Exercises 4552, determine if the graph can...Ch. 3.2 - For Exercises 4552, determine if the graph can...Ch. 3.2 - Prob. 49PECh. 3.2 - Prob. 50PECh. 3.2 - Prob. 51PECh. 3.2 - Prob. 52PECh. 3.2 - For Exercises 5358, a. Identify the power function...Ch. 3.2 - Prob. 54PECh. 3.2 - For Exercises 5358, a. Identify the power function...Ch. 3.2 - Prob. 56PECh. 3.2 - For Exercises 5358, a. Identify the power function...Ch. 3.2 - Prob. 58PECh. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - Prob. 60PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 64PECh. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - Prob. 68PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 70PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 72PECh. 3.2 - For Exercises 59–76, sketch the function. (See...Ch. 3.2 - Prob. 74PECh. 3.2 - For Exercises 5976, sketch the function. (See...Ch. 3.2 - Prob. 76PECh. 3.2 - Prob. 77PECh. 3.2 - For Exercises 77–88, determine if the statement is...Ch. 3.2 - For Exercises 77–88, determine if the statement is...Ch. 3.2 - For Exercises 7788, determine if the statement is...Ch. 3.2 - For Exercises 7788, determine if the statement is...Ch. 3.2 - Prob. 82PECh. 3.2 - Prob. 83PECh. 3.2 - Prob. 84PECh. 3.2 - Prob. 85PECh. 3.2 - Prob. 86PECh. 3.2 - Prob. 87PECh. 3.2 - For Exercises 7788, determine if the statement is...Ch. 3.2 - 89. A rocket will carry a communications satellite...Ch. 3.2 - 90. Data from a 20-yr study show the number of new...Ch. 3.2 - 91. Given a polynomial function defined by,...Ch. 3.2 - Write an informal explanation of what it means for...Ch. 3.2 - Prob. 93PECh. 3.2 - Prob. 94PECh. 3.2 - Prob. 95PECh. 3.2 - Prob. 96PECh. 3.2 - Prob. 97PECh. 3.2 - 98. The torque (in ft-lb) produced by a certain...Ch. 3.2 - Prob. 99PECh. 3.2 - Prob. 100PECh. 3.2 - Prob. 101PECh. 3.2 - Prob. 102PECh. 3.2 - For Exercises 102–103, graph the function defined...Ch. 3.3 - Skill Practice 1 Use long division to divide. Ch. 3.3 - Skill Practice 2 Use long division to divide....Ch. 3.3 - Skill Practice 3 Use long division to divide. Ch. 3.3 - Skill Practice 4 Use synthetic division to...Ch. 3.3 - Skill Practice 5 Use synthetic division to...Ch. 3.3 - Skill Practice 6 Given use the remainder theorem...Ch. 3.3 - Skill Practice 7 Use the remainder theorem to...Ch. 3.3 - Skill Practice 8 Use the factor theorem to...Ch. 3.3 - Skill Practice 9 a. Factor, given that –4 is a...Ch. 3.3 - Skill Practice 10 Write a polynomial f(x) of...Ch. 3.3 - Prob. 1PECh. 3.3 - Prob. 2PECh. 3.3 - Prob. 3PECh. 3.3 - Prob. 4PECh. 3.3 - Prob. 5PECh. 3.3 - Prob. 6PECh. 3.3 - Prob. 7PECh. 3.3 - For Exercises 7–8, (See Example 1) a. Use long...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - Prob. 18PECh. 3.3 - For Exercises 922, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 9–22, use long division to divide,...Ch. 3.3 - For Exercises 2326, consider the division of two...Ch. 3.3 - Prob. 24PECh. 3.3 - For Exercises 2326, consider the division of two...Ch. 3.3 - Prob. 26PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - For Exercises 2738, use synthetic division to...Ch. 3.3 - For Exercises 2738, use synthetic division to...Ch. 3.3 - Prob. 30PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - Prob. 32PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - Prob. 34PECh. 3.3 - For Exercises 2738, use synthetic division to...Ch. 3.3 - Prob. 36PECh. 3.3 - For Exercises 27–38, use synthetic division to...Ch. 3.3 - Prob. 38PECh. 3.3 - 39. The value for a polynomial. What can be...Ch. 3.3 - Prob. 40PECh. 3.3 - 41. Given. a. Evaluate. b. Determine the...Ch. 3.3 - Prob. 42PECh. 3.3 - For Exercises 4346, use the remainder theorem to...Ch. 3.3 - For Exercises 4346, use the remainder theorem to...Ch. 3.3 - For Exercises 43–46, use the remainder theorem to...Ch. 3.3 - Prob. 46PECh. 3.3 - For Exercises 4754, use the remainder theorem to...Ch. 3.3 - Prob. 48PECh. 3.3 - For Exercises 47–54, use the remainder theorem to...Ch. 3.3 - Prob. 50PECh. 3.3 - For Exercises 47–54, use the remainder theorem to...Ch. 3.3 - For Exercises 4754, use the remainder theorem to...Ch. 3.3 - For Exercises 47–54, use the remainder theorem to...Ch. 3.3 - Prob. 54PECh. 3.3 - For Exercises 55–60, use the factor theorem to...Ch. 3.3 - Prob. 56PECh. 3.3 - For Exercises 5560, use the factor theorem to...Ch. 3.3 - Prob. 58PECh. 3.3 - For Exercises 55–60, use the factor theorem to...Ch. 3.3 - Prob. 60PECh. 3.3 - 61. Given, a. Evaluate. b. Evaluate. c. Solve....Ch. 3.3 - Prob. 62PECh. 3.3 - a. Use synthetic division and the factor theorem...Ch. 3.3 - Prob. 64PECh. 3.3 - a. Factor f(x)=2x2+x237x36, given that 1is a zero....Ch. 3.3 - Prob. 66PECh. 3.3 - 67. a. Factor is a zero. b. Solve. Ch. 3.3 - 68. a. Factor is a zero. b. Solve. Ch. 3.3 - 69. a. Factor, given that 3 is a zero. b. Solve....Ch. 3.3 - Prob. 70PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 72PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 74PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 76PECh. 3.3 - For Exercises 71–82, write a polynomial that meets...Ch. 3.3 - Prob. 78PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 80PECh. 3.3 - For Exercises 7182, write a polynomial f(x) that...Ch. 3.3 - Prob. 82PECh. 3.3 - Prob. 83PECh. 3.3 - Prob. 84PECh. 3.3 - Prob. 85PECh. 3.3 - Prob. 86PECh. 3.3 - Prob. 87PECh. 3.3 - Prob. 88PECh. 3.3 - Prob. 89PECh. 3.3 - Prob. 90PECh. 3.3 - Prob. 91PECh. 3.3 - Prob. 92PECh. 3.3 - Prob. 93PECh. 3.3 - Prob. 94PECh. 3.3 - Prob. 95PECh. 3.3 - Prob. 96PECh. 3.3 - Prob. 97PECh. 3.3 - How can the division algorithm be used to check...Ch. 3.3 - Prob. 99PECh. 3.3 - Prob. 100PECh. 3.3 - Prob. 101PECh. 3.3 - Prob. 102PECh. 3.3 - Prob. 103PECh. 3.3 - Prob. 104PECh. 3.3 - Prob. 105PECh. 3.3 - Prob. 106PECh. 3.4 - Skill Practice 1 List all possible rational zeros....Ch. 3.4 - Skill Practice 2 Find the zeros. f(x)=x3x24x2Ch. 3.4 - Skill Practice 3 Find the zeros and their...Ch. 3.4 - Skill Practice 4 Find the zeros. Ch. 3.4 - Skill Practice 5 Given, and that is a zero of. a....Ch. 3.4 - Skill Practice 6 a. Find a third-degree...Ch. 3.4 - Skill Practice 7 Determine the number of possible...Ch. 3.4 - Skill Practice 8 Determine the number of possible...Ch. 3.4 - Skill Practice 9 Given f(x)=x42x313x24x30. a....Ch. 3.4 - Skill Practice 10 Find the zeros and their...Ch. 3.4 - Prob. 1PECh. 3.4 - If f(x) is a polynomial of degree n1 with complex...Ch. 3.4 - Prob. 3PECh. 3.4 - A real number b is called an __________ bound of...Ch. 3.4 - Prob. 5PECh. 3.4 - Prob. 6PECh. 3.4 - For Exercises 7–12, list the possible rational...Ch. 3.4 - For Exercises 712, list the possible rational...Ch. 3.4 - For Exercises 7–12, list the possible rational...Ch. 3.4 - Prob. 10PECh. 3.4 - For Exercises 712, list the possible rational...Ch. 3.4 - For Exercises 712, list the possible rational...Ch. 3.4 - Which of the following is not a possible zero of...Ch. 3.4 - 14. Which of the following is not a possible zero...Ch. 3.4 - For Exercises 15–16, find all the rational zeros....Ch. 3.4 - For Exercises 15–16, find all the rational zeros....Ch. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - Prob. 18PECh. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - Prob. 24PECh. 3.4 - For Exercises 1728, find all the zeros. (See...Ch. 3.4 - Prob. 26PECh. 3.4 - For Exercises 17–28, find all the zeros. (See...Ch. 3.4 - Prob. 28PECh. 3.4 - Prob. 29PECh. 3.4 - Prob. 30PECh. 3.4 - If f(x) is a polynomial with real coefficients and...Ch. 3.4 - Prob. 32PECh. 3.4 - Prob. 33PECh. 3.4 - Prob. 34PECh. 3.4 - For Exercises 3338, a polynomial f(x) and one or...Ch. 3.4 - Prob. 36PECh. 3.4 - For Exercises 33–38, a polynomial and one or more...Ch. 3.4 - Prob. 38PECh. 3.4 - For Exercises 39–48, write a polynomial that...Ch. 3.4 - For Exercises 39–48, write a polynomial that...Ch. 3.4 - For Exercises 39–48, write a polynomial that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - Prob. 46PECh. 3.4 - For Exercises 3948, write a polynomial f(x) that...Ch. 3.4 - Prob. 48PECh. 3.4 - Prob. 49PECh. 3.4 - Prob. 50PECh. 3.4 - Prob. 51PECh. 3.4 - Prob. 52PECh. 3.4 - Prob. 53PECh. 3.4 - Prob. 54PECh. 3.4 - Prob. 55PECh. 3.4 - Prob. 56PECh. 3.4 - Prob. 57PECh. 3.4 - Prob. 58PECh. 3.4 - Prob. 59PECh. 3.4 - Prob. 60PECh. 3.4 - Prob. 61PECh. 3.4 - For Exercises 59–64, (See Example 9) a. Determine...Ch. 3.4 - Prob. 63PECh. 3.4 - Prob. 64PECh. 3.4 - Prob. 65PECh. 3.4 - Prob. 66PECh. 3.4 - Prob. 67PECh. 3.4 - For Exercises 65–68, determine if the statement is...Ch. 3.4 - Prob. 69PECh. 3.4 - Prob. 70PECh. 3.4 - Prob. 71PECh. 3.4 - Fir Exercises 69–84, find the zeros and their...Ch. 3.4 - Prob. 73PECh. 3.4 - Fir Exercises 6984, find the zeros and their...Ch. 3.4 - Prob. 75PECh. 3.4 - Prob. 76PECh. 3.4 - Prob. 77PECh. 3.4 - Prob. 78PECh. 3.4 - Prob. 79PECh. 3.4 - Fir Exercises 69–84, find the zeros and their...Ch. 3.4 - Prob. 81PECh. 3.4 - Prob. 82PECh. 3.4 - Fir Exercises 6984, find the zeros and their...Ch. 3.4 - Prob. 84PECh. 3.4 - Prob. 85PECh. 3.4 - Prob. 86PECh. 3.4 - Prob. 87PECh. 3.4 - Prob. 88PECh. 3.4 - Prob. 89PECh. 3.4 - Prob. 90PECh. 3.4 - Prob. 91PECh. 3.4 - Prob. 92PECh. 3.4 - Prob. 93PECh. 3.4 - Prob. 94PECh. 3.4 - Prob. 95PECh. 3.4 - Prob. 96PECh. 3.4 - Prob. 97PECh. 3.4 - Prob. 98PECh. 3.4 - Prob. 99PECh. 3.4 - Prob. 100PECh. 3.4 - The front face of a tent is triangular and the...Ch. 3.4 - Prob. 102PECh. 3.4 - Prob. 103PECh. 3.4 - Prob. 104PECh. 3.4 - Prob. 105PECh. 3.4 - Prob. 106PECh. 3.4 - Prob. 107PECh. 3.4 - Prob. 108PECh. 3.4 - Prob. 109PECh. 3.4 - Prob. 110PECh. 3.4 - Prob. 111PECh. 3.4 - Find all sixth roots of 1, by solving the equation...Ch. 3.4 - Use the rational zero theorem to show that 5 is an...Ch. 3.4 - Prob. 114PECh. 3.4 - Prob. 115PECh. 3.4 - Foe Exercises 115116, use the formula...Ch. 3.5 - Skill Practice 1 The graph of is given. a. As...Ch. 3.5 - Skill Practice 2 Identify the vertical...Ch. 3.5 - Skill Practice 3 Find the horizontal asymptotes...Ch. 3.5 - Skill Practice 4 Given g(x)=3x2+4x3x2+3, determine...Ch. 3.5 - Skill Practice 5 Determine the asymptotes. Ch. 3.5 - Skill Practice 6 Use transformations to graph. Ch. 3.5 - Skill Practice 7 Graph f(x)=x1x+4.Ch. 3.5 - Skill Practice 8 Graph g(x)=5xx29.Ch. 3.5 - Skill Practice 9 Graph g(x)=4x2+7x2x2+4.Ch. 3.5 - Skill Practice 10 Graph k(x)=2x27x+3x2.Ch. 3.5 - Skill Practice 11 Repeat Example 11 under the...Ch. 3.5 - Prob. 1PECh. 3.5 - 2. The notation is read as _________. Ch. 3.5 - Prob. 3PECh. 3.5 - Prob. 4PECh. 3.5 - Prob. 5PECh. 3.5 - Prob. 6PECh. 3.5 - For Exercises 712, write the domain of the...Ch. 3.5 - For Exercises 712, write the domain of the...Ch. 3.5 - For Exercises 7–12, write the domain of the...Ch. 3.5 - For Exercises 712, write the domain of the...Ch. 3.5 - For Exercises 7–12, write the domain of the...Ch. 3.5 - Prob. 12PECh. 3.5 - Prob. 13PECh. 3.5 - Prob. 14PECh. 3.5 - Prob. 15PECh. 3.5 - For Exercises 1316, refer to the graph of the...Ch. 3.5 - For Exercises 17–24, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - For Exercises 17–24, determine the vertical...Ch. 3.5 - For Exercises 17–24, determine the vertical...Ch. 3.5 - For Exercises 1724, determine the vertical...Ch. 3.5 - Prob. 24PECh. 3.5 - 25. The graph of will behave like which function...Ch. 3.5 - Prob. 26PECh. 3.5 - 27. The graph of will behave like which function...Ch. 3.5 - Prob. 28PECh. 3.5 - For Exercises 2936, a. Identify the horizontal...Ch. 3.5 - Prob. 30PECh. 3.5 - For Exercises 29–36, a. Identify the horizontal...Ch. 3.5 - For Exercises 2936, a. Identify the horizontal...Ch. 3.5 - For Exercises 2936, a. Identify the horizontal...Ch. 3.5 - Prob. 34PECh. 3.5 - For Exercises 29–36, a. Identify the horizontal...Ch. 3.5 - Prob. 36PECh. 3.5 - Prob. 37PECh. 3.5 - Prob. 38PECh. 3.5 - For Exercises 39–48, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 39–48, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - For Exercises 3948, identify the asymptotes. (See...Ch. 3.5 - Prob. 46PECh. 3.5 - Prob. 47PECh. 3.5 - Prob. 48PECh. 3.5 - Prob. 49PECh. 3.5 - Prob. 50PECh. 3.5 - Prob. 51PECh. 3.5 - Prob. 52PECh. 3.5 - Prob. 53PECh. 3.5 - Prob. 54PECh. 3.5 - Prob. 55PECh. 3.5 - Prob. 56PECh. 3.5 - Prob. 57PECh. 3.5 - For Exercises 5762, for the graph of y=f(x). a....Ch. 3.5 - For Exercises 5762, for the graph of y=f(x). a....Ch. 3.5 - Prob. 60PECh. 3.5 - Prob. 61PECh. 3.5 - For Exercises 57–62, for the graph...Ch. 3.5 - Prob. 63PECh. 3.5 - Prob. 64PECh. 3.5 - Prob. 65PECh. 3.5 - Prob. 66PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 68PECh. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - Prob. 70PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 72PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 74PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 78PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 80PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - Prob. 84PECh. 3.5 - For Exercises 67–90, graph the function. (See...Ch. 3.5 - Prob. 86PECh. 3.5 - For Exercises 6790, graph the function. (See...Ch. 3.5 - Prob. 88PECh. 3.5 - Prob. 89PECh. 3.5 - Prob. 90PECh. 3.5 - 91. A sports trainer has monthly costs of $69.95...Ch. 3.5 - Prob. 92PECh. 3.5 - Prob. 93PECh. 3.5 - Prob. 94PECh. 3.5 - Prob. 95PECh. 3.5 - A certain diet pill is designed to delay the...Ch. 3.5 - Prob. 97PECh. 3.5 - 98. The cost (in $1000) for a city to remove x%...Ch. 3.5 - The Doppler effect is a change in the observed...Ch. 3.5 - The Doppler effect is a change in the observed...Ch. 3.5 - Prob. 101PECh. 3.5 - Prob. 102PECh. 3.5 - Prob. 103PECh. 3.5 - Prob. 104PECh. 3.5 - Prob. 105PECh. 3.5 - Prob. 106PECh. 3.5 - Prob. 107PECh. 3.5 - Prob. 108PECh. 3.5 - Prob. 109PECh. 3.5 - Prob. 110PECh. 3.5 - The rational functions studied in this section all...Ch. 3.5 - The rational functions studied in this section all...Ch. 3.5 - The rational functions studied in this section all...Ch. 3.5 - Prob. 114PECh. 3.5 - Prob. 1PRECh. 3.5 - Prob. 2PRECh. 3.5 - Prob. 3PRECh. 3.5 - Prob. 4PRECh. 3.5 - Prob. 5PRECh. 3.5 - Prob. 6PRECh. 3.5 - Prob. 7PRECh. 3.5 - Prob. 8PRECh. 3.5 - Prob. 9PRECh. 3.5 - Prob. 10PRECh. 3.5 - Prob. 11PRECh. 3.5 - For Exercises 916, refer to...Ch. 3.5 - Prob. 13PRECh. 3.5 - Prob. 14PRECh. 3.5 - Prob. 15PRECh. 3.5 - Prob. 16PRECh. 3.5 - Prob. 17PRECh. 3.5 - Prob. 18PRECh. 3.5 - Prob. 19PRECh. 3.5 - Prob. 20PRECh. 3.5 - Prob. 21PRECh. 3.5 - Prob. 22PRECh. 3.6 - Skill Practice 1 Solve the inequality. Ch. 3.6 - Skill Practice 2 Solve the inequality. x418x3x24x3Ch. 3.6 - Prob. 3SPCh. 3.6 - Skill Practice 4 Solve the inequality. Ch. 3.6 - Skill Practice 5 Solve the inequality. Ch. 3.6 - Skill Practice 6 Solve the inequalities. a. ...Ch. 3.6 - Skill Practice 7 Repeat Example 7 under the...Ch. 3.6 - 1. Let be a polynomial. An inequality of the form ...Ch. 3.6 - Prob. 2PECh. 3.6 - Prob. 3PECh. 3.6 - Prob. 4PECh. 3.6 - Prob. 5PECh. 3.6 - For Exercises 514, the graph of y=f(x) is given....Ch. 3.6 - Prob. 7PECh. 3.6 - For Exercises 514, the graph of y=f(x) is given....Ch. 3.6 - Prob. 9PECh. 3.6 - For Exercises 5–14, the graph of is given. Solve...Ch. 3.6 - Prob. 11PECh. 3.6 - For Exercises 514, the graph of y=f(x) is given....Ch. 3.6 - Prob. 13PECh. 3.6 - Prob. 14PECh. 3.6 - Prob. 15PECh. 3.6 - Prob. 16PECh. 3.6 - For Exercises 1520, solve the equations and...Ch. 3.6 - For Exercises 15–20, solve the equations and...Ch. 3.6 - For Exercises 15–20, solve the equations and...Ch. 3.6 - Prob. 20PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 22PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 24PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 26PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 28PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 30PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 36PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 38PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 40PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 44PECh. 3.6 - For Exercises 2154, solve the inequalities. (See...Ch. 3.6 - Prob. 46PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 50PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 52PECh. 3.6 - For Exercises 21–54, solve the inequalities. (See...Ch. 3.6 - Prob. 54PECh. 3.6 - Prob. 55PECh. 3.6 - Prob. 56PECh. 3.6 - Prob. 57PECh. 3.6 - Prob. 58PECh. 3.6 - For Exercises 5962, solve the inequalities. (See...Ch. 3.6 - Prob. 60PECh. 3.6 - For Exercises 5962, solve the inequalities. (See...Ch. 3.6 - Prob. 62PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 64PECh. 3.6 - For Exercises 63–84, solve the inequalities. (See...Ch. 3.6 - Prob. 66PECh. 3.6 - For Exercises 63–84, solve the inequalities. (See...Ch. 3.6 - Prob. 68PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 70PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 72PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 74PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 76PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 78PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 80PECh. 3.6 - For Exercises 6384, solve the inequalities. (See...Ch. 3.6 - Prob. 82PECh. 3.6 - For Exercises 63–84, solve the inequalities. (See...Ch. 3.6 - Prob. 84PECh. 3.6 - Prob. 85PECh. 3.6 - 86. Suppose that a basketball player jumps...Ch. 3.6 - Prob. 87PECh. 3.6 - 88. The population of a bacteria culture is given...Ch. 3.6 - 89. Suppose that an object that is originally at...Ch. 3.6 - The average round trip speed S (in mph) of a...Ch. 3.6 - 91. A rectangular quilt is to be made so that the...Ch. 3.6 - A landscaping team plans to build a rectangular...Ch. 3.6 - Prob. 93PECh. 3.6 - Prob. 94PECh. 3.6 - Prob. 95PECh. 3.6 - Prob. 96PECh. 3.6 - Prob. 97PECh. 3.6 - Prob. 98PECh. 3.6 - Prob. 99PECh. 3.6 - Prob. 100PECh. 3.6 - Prob. 101PECh. 3.6 - Prob. 102PECh. 3.6 - Prob. 103PECh. 3.6 - Prob. 104PECh. 3.6 - Prob. 105PECh. 3.6 - Prob. 106PECh. 3.6 - Prob. 107PECh. 3.6 - Prob. 108PECh. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - Prob. 114PECh. 3.6 - Prob. 115PECh. 3.6 - Prob. 116PECh. 3.6 - Prob. 117PECh. 3.6 - The procedure to solve a polynomial or rational...Ch. 3.6 - Prob. 119PECh. 3.6 - Prob. 120PECh. 3.6 - Prob. 121PECh. 3.6 - Prob. 122PECh. 3.6 - Prob. 123PECh. 3.6 - 124. The concentration of a drug in the...Ch. 3.6 - Prob. 1PRECh. 3.6 - Prob. 2PRECh. 3.6 - Prob. 3PRECh. 3.6 - Prob. 4PRECh. 3.6 - Prob. 5PRECh. 3.6 - Prob. 6PRECh. 3.6 - Prob. 7PRECh. 3.6 - Prob. 8PRECh. 3.6 - Prob. 9PRECh. 3.6 - Prob. 10PRECh. 3.6 - Prob. 11PRECh. 3.6 - Prob. 12PRECh. 3.6 - Prob. 13PRECh. 3.6 - Prob. 14PRECh. 3.6 - Prob. 15PRECh. 3.6 - Prob. 16PRECh. 3.6 - Prob. 17PRECh. 3.6 - Prob. 18PRECh. 3.6 - Prob. 19PRECh. 3.6 - Prob. 20PRECh. 3.6 - Prob. 21PRECh. 3.6 - Prob. 22PRECh. 3.6 - Prob. 23PRECh. 3.6 - Prob. 24PRECh. 3.6 - Prob. 25PRECh. 3.6 - Prob. 26PRECh. 3.6 - Prob. 27PRECh. 3.6 - Prob. 28PRECh. 3.6 - Prob. 29PRECh. 3.6 - At this point in the text, we have studied several...Ch. 3.7 - Skill Practice 1 Write a variation model using k...Ch. 3.7 - Prob. 2SPCh. 3.7 - Skill Practice 3 The amount of the medicine...Ch. 3.7 - Prob. 4SPCh. 3.7 - Prob. 5SPCh. 3.7 - Prob. 1PECh. 3.7 - Prob. 2PECh. 3.7 - Prob. 3PECh. 3.7 - Prob. 4PECh. 3.7 - Prob. 5PECh. 3.7 - Prob. 6PECh. 3.7 - Prob. 7PECh. 3.7 - Prob. 8PECh. 3.7 - Prob. 9PECh. 3.7 - Prob. 10PECh. 3.7 - Prob. 11PECh. 3.7 - For Exercises 11–20, write a variation model using...Ch. 3.7 - Prob. 13PECh. 3.7 - Prob. 14PECh. 3.7 - For Exercises 11–20, write a variation model using...Ch. 3.7 - Prob. 16PECh. 3.7 - Prob. 17PECh. 3.7 - Prob. 18PECh. 3.7 - Prob. 19PECh. 3.7 - For Exercises 11–20, write a variation model using...Ch. 3.7 - Prob. 21PECh. 3.7 - Prob. 22PECh. 3.7 - For Exercises 21–26, find the constant of...Ch. 3.7 - Prob. 24PECh. 3.7 - Prob. 25PECh. 3.7 - Prob. 26PECh. 3.7 - Prob. 27PECh. 3.7 - Prob. 28PECh. 3.7 - Prob. 29PECh. 3.7 - Prob. 30PECh. 3.7 - Prob. 31PECh. 3.7 - Prob. 32PECh. 3.7 - For Exercises 2948, use a variation model to solve...Ch. 3.7 - Prob. 34PECh. 3.7 - Prob. 35PECh. 3.7 - Prob. 36PECh. 3.7 - For Exercises 29–48, use a variation model to...Ch. 3.7 - Prob. 38PECh. 3.7 - Prob. 39PECh. 3.7 - For Exercises 29–48, use a variation model to...Ch. 3.7 - Prob. 41PECh. 3.7 - Prob. 42PECh. 3.7 - Prob. 43PECh. 3.7 - Prob. 44PECh. 3.7 - Prob. 45PECh. 3.7 - For Exercises 2948, use a variation model to solve...Ch. 3.7 - Prob. 47PECh. 3.7 - For Exercises 29–48, use a variation model to...Ch. 3.7 - Prob. 49PECh. 3.7 - Prob. 50PECh. 3.7 - Prob. 51PECh. 3.7 - Prob. 52PECh. 3.7 - 53. Which formula (s) can represent a variation...Ch. 3.7 - Prob. 54PECh. 3.7 - Prob. 55PECh. 3.7 - Prob. 56PECh. 3.7 - Prob. 57PECh. 3.7 - Prob. 58PECh. 3.7 - Prob. 59PECh. 3.7 - Prob. 60PECh. 3.7 - Prob. 61PECh. 3.7 - Prob. 62PECh. 3.7 - Prob. 63PECh. 3.7 - Prob. 64PECh. 3 - Given f(x)=(x+5)2+2, identify the vertex of the...Ch. 3 - For Exercises 2–3, a. Write the equation in...Ch. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Suppose that p is the probability that a randomly...Ch. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - For Exercises 8–11, a. Determine the end behavior...Ch. 3 - 12. Determine whether the intermediate value...Ch. 3 - Prob. 13RECh. 3 - For Exercises 1316, determine if the statement is...Ch. 3 - For Exercises 13–16, determine if the statement is...Ch. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Prob. 28RECh. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Prob. 38RECh. 3 - Prob. 39RECh. 3 - Prob. 40RECh. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Prob. 43RECh. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RECh. 3 - Prob. 47RECh. 3 - For Exercises 4851, graph the function. f(x)=1x4+2Ch. 3 - For Exercises 4851, graph the function....Ch. 3 - Prob. 50RECh. 3 - For Exercises 48–51, graph the function. 51. Ch. 3 - After taking a certain class. The percentage of...Ch. 3 - Prob. 53RECh. 3 - Prob. 54RECh. 3 - Prob. 55RECh. 3 - Prob. 56RECh. 3 - Prob. 57RECh. 3 - Prob. 58RECh. 3 - Prob. 59RECh. 3 - Prob. 60RECh. 3 - Prob. 61RECh. 3 - Prob. 62RECh. 3 - Prob. 63RECh. 3 - Prob. 64RECh. 3 - Prob. 65RECh. 3 - Prob. 66RECh. 3 - 67. A sports trainer has monthly casts of $80 for...Ch. 3 - A child throws a ball straight upwards to his...Ch. 3 - Prob. 69RECh. 3 - For Exercises 69–71, write a variation model...Ch. 3 - Prob. 71RECh. 3 - Prob. 72RECh. 3 - Prob. 73RECh. 3 - Prob. 74RECh. 3 - Prob. 75RECh. 3 - Prob. 76RECh. 3 - Prob. 77RECh. 3 - 1. Given. a. Write the equation in vertex form:...Ch. 3 - Prob. 2TCh. 3 - Prob. 3TCh. 3 - Prob. 4TCh. 3 - Prob. 5TCh. 3 - Prob. 6TCh. 3 - Prob. 7TCh. 3 - Given f(x)=x48x3+21x232x+68 and that 2i is a zero...Ch. 3 - Given f(x)=3x4+7x312x214x+12, a. How many zeros...Ch. 3 - Prob. 10TCh. 3 - Determine the number of possible positive and...Ch. 3 - Prob. 12TCh. 3 - Prob. 13TCh. 3 - For Exercises 12–14, determine the asymptotes...Ch. 3 - Prob. 15TCh. 3 - Prob. 16TCh. 3 - For Exercises 15–17, graph the function, 17. Ch. 3 - Prob. 18TCh. 3 - Prob. 19TCh. 3 - Prob. 20TCh. 3 - Prob. 21TCh. 3 - Prob. 22TCh. 3 - Prob. 23TCh. 3 - Prob. 24TCh. 3 - Prob. 25TCh. 3 - Prob. 26TCh. 3 - Prob. 27TCh. 3 - The weight of a body varies inversely as the...Ch. 3 - Prob. 29TCh. 3 - Prob. 30TCh. 3 - Prob. 31TCh. 3 - Suppose that a rocket is shot straight upward from...Ch. 3 - 33. The number of yearly visits to physicians’...Ch. 3 - Given r(x)=2x23x216, a. Find the vertical...Ch. 3 - Find a polynomial f(x) of lowest degree with real...Ch. 3 - Given f(x)=2x3x28x5, a. Determine the end behavior...Ch. 3 - 4. Divide and write the answer in the form Ch. 3 - Prob. 5CRECh. 3 - 6. Determine an equation of the line passing...Ch. 3 - Prob. 7CRECh. 3 - Graph f(x)={x1forx1x1forx1Ch. 3 - Prob. 9CRECh. 3 - 10. Given, a. Find the x-intercepts. b. Find the...Ch. 3 - Prob. 11CRECh. 3 - For Exercises 1214, simplify the expression....Ch. 3 - Prob. 13CRECh. 3 - Prob. 14CRECh. 3 - Prob. 15CRECh. 3 - Prob. 16CRECh. 3 - Prob. 17CRECh. 3 - Prob. 18CRECh. 3 - Prob. 19CRECh. 3 - Prob. 20CRE
Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
SEE MORE TEXTBOOKS
Interpreting Graphs of Quadratic Equations (GMAT/GRE/CAT/Bank PO/SSC CGL) | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=BHgewRcuoRM;License: Standard YouTube License, CC-BY
Solve a Trig Equation in Quadratic Form Using the Quadratic Formula (Cosine, 4 Solutions); Author: Mathispower4u;https://www.youtube.com/watch?v=N6jw_i74AVQ;License: Standard YouTube License, CC-BY