
Concept explainers
An athlete whose is the shot put releases the shot with the same initial velocity but at different angles. The figure shows the parabolic paths for shots released at angles of
, Exercises 57-58 are based on the functions that model the parabolic paths.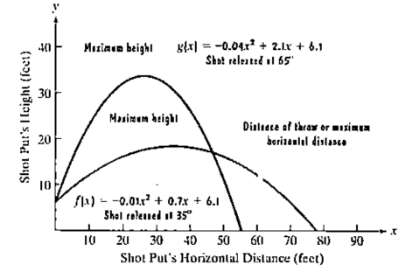
when the shot whose path is shown by the blue graph is released at an angle of
where x is the shot’s horizontal distance, in feet from its point of release. Use this model to solve parts (a) through (c) and verify yours answers using the blue graph.
a. What is the maximum height of the shot and how far from its point of release does this occur?
b. What is the shot’s maximum horizontal distance, to the nearest tenth of foot, or the distance of the throw?
c. From what height was the shot released?
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Blitzer Algebra And Trigonometry, 6th Edition, 9780134585291, 0134585291, 2018
Additional Math Textbook Solutions
Math in Our World
Algebra and Trigonometry (6th Edition)
Elementary & Intermediate Algebra
A First Course in Probability (10th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
- 4. [9 points] Assume that B, C, E are all 3 x 3 matrices such that BC == -64 -1 0 3 4 4 4 -2 2 CB=-1-2 4 BE -2 1 3 EC = 1 3 2 -7, 1 6 -6 2-5 -7 -2 Explicitly compute the following by hand. (I.e., write out the entries of the 3 × 3 matrix.) (a) [3 points] B(E+C) (b) [3 points] (E+B)C (c) [3 points] ETBTarrow_forward6. Consider the matrices G = 0 (3) -3\ -3 2 and H = -1 2 0 5 0 5 5 noting that H(:, 3) = 2H(:,1) + H(:, 2). Is G invertible? Explain your answer. Is H invertible? Explain your answer. Use co-factor expansion to find the determinant of H. (Hint: expand the 2nd or 3rd row)arrow_forwardFor the matrix A = = ( 6 }) . explicitly compute by hand (with work shown) the following. I2A, where I2 is the 2 × 2 identity matrix. A-1 solving the following linear systems by using A-¹: c+y= 1 y = 1 (d) (e) (f) A² find the diagonal entries of Aarrow_forward
- If 3x−y=12, what is the value of 8x / 2y A) 212B) 44C) 82D) The value cannot be determined from the information given.arrow_forwardC=59(F−32) The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true? A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius. A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit. A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius. A) I onlyB) II onlyC) III onlyD) I and II onlyarrow_forward(1) Let F be a field, show that the vector space F,NEZ* be a finite dimension. (2) Let P2(x) be the vector space of polynomial of degree equal or less than two and M={a+bx+cx²/a,b,cЄ R,a+b=c),show that whether Mis hyperspace or not. (3) Let A and B be a subset of a vector space such that ACB, show that whether: (a) if A is convex then B is convex or not. (b) if B is convex then A is convex or not. (4) Let R be a field of real numbers and X=R, X is a vector space over R show that by definition the norms/II.II, and II.112 on X are equivalent where Ilxll₁ = max(lx,l, i=1,2,...,n) and llxll₂=(x²). oper (5) Let Ⓡ be a field of real numbers, Ⓡis a normed space under usual operations and norm, let E=(2,5,8), find int(E), b(E) and D(E). (6) Write the definition of bounded linear function between two normed spaces and write with prove the relation between continuous and bounded linear function between two normed spaces.arrow_forward
- ind → 6 Q₁/(a) Let R be a field of real numbers and X-P(x)=(a+bx+cx²+dx/ a,b,c,dER},X is a vector space over R, show that is finite dimension. (b) Let be a bijective linear function from a finite dimension vector ✓ into a space Yand Sbe a basis for X, show that whether f(S) basis for or not. (c) Let be a vector space over a field F and A,B)affine subsets of X,show that whether aAn BB, aAU BB be affine subsets of X or not, a,ẞ EF. (12 Jal (answer only two) (6) Let M be a non-empty subset of a vector space X and tEX, show that M is a hyperspace of X iff t+M is a hyperplane of X and tЄt+M. (b) State Jahn-Banach theorem and write with prove an application of Hahn-arrow_forward(b) Let A and B be two subset of a linear space X such that ACB, show that whether if A is affine set then B affine or need not and if B affine set then A affine set or need not. Qz/antonly be a-Show that every hyperspace of a vecor space X is hyperplane but the convers need not to be true. b- Let M be a finite dimension subspace of a Banach space X show that M is closed set. c-Show that every two norms on finite dimension vector space are equivant (1) Q/answer only two a-Write the definition of bounded set in: a normed space and write with prove an equivalent statement to a definition. b- Let f be a function from a normed space X into a normed space Y, show that f continuous iff f is bounded. c-Show that every finite dimension normed space is a Banach. Q/a- Let A and B two open sets in a normed space X, show that by definition AnB and AUB are open sets. (1 nood truearrow_forwardlog (6x+5)-log 3 = log 2 - log xarrow_forward
- 1 The ratio of Argan to Potassium from a sample found sample found in Canada is .195 Find The estimated age of the sample A In (1+8.33 (+)) t = (1-26 × 109) en (1 In aarrow_forward7. Find the doubling time of an investment earning 2.5% interest compounded a) semiannually b) continuouslyarrow_forward6. Find the time it will take $1000 to grow to $5000 at an interest rate of 3.5% if the interest is compounded a) quarterly b) continuouslyarrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

