Pearson eText for Calculus & Its Applications -- Instant Access (Pearson+)
15th Edition
ISBN: 9780137590728
Author: Larry Goldstein, David Lay
Publisher: PEARSON+
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.1, Problem 32E
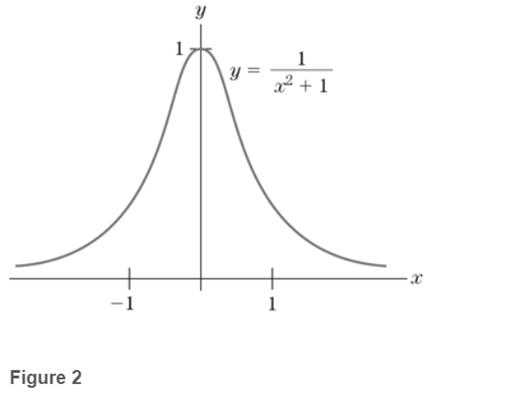
Find the inflection points on the graph of
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Sketch a possible graph of a function f, together with vertical asymptotes, that satisfies all of the following conditions.
f(2)=0
f(4) is undefined
lim f(x)=1
X-6
lim f(x) = -∞
x-0+
lim f(x) = ∞
lim f(x) = ∞
x-4
_8
Determine the following limit.
lim
35w² +8w+4
w→∞ √49w+w³
3
Select the correct choice below, and, if necessary, fill in the answer box to complete your choice.
○ A.
lim
W→∞
35w² +8w+4
49w+w3
(Simplify your answer.)
B. The limit does not exist and is neither ∞ nor - ∞.
Calculate the limit lim
X-a
x-a
5
using the following factorization formula where n is a positive integer and
x-➡a
a is a real number.
x-a = (x-a) (x1+x-2a+x
lim
x-a
X - a
x-a
5
=
n-
+ xa
an-2 + an−1)
Chapter 3 Solutions
Pearson eText for Calculus & Its Applications -- Instant Access (Pearson+)
Ch. 3.1 - Consider the function y=(x+1)x. Differentiate y by...Ch. 3.1 - Prob. 2CYUCh. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28. y=xxCh. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28. y=[...
Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Prob. 18ECh. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28. y=[...Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Differentiate the functions in Exercise 1-28....Ch. 3.1 - Find the equation of the tangent line to the curve...Ch. 3.1 - Find the equation of the tangent line to the curve...Ch. 3.1 - Find all x-coordinates of points (x,y) on the...Ch. 3.1 - Find the inflection points on the graph of...Ch. 3.1 - Find all x such that dydx=0, where...Ch. 3.1 - The graph of y=(x21)4(x2+1)5 is shown in Fig. 3....Ch. 3.1 - Find the point(s) on the graph of y=(x2+3x1)/x...Ch. 3.1 - Find the point(s) on the graph of y=(2x4+1)(x5)...Ch. 3.1 - Find d2ydx2. y=(x2+1)4Ch. 3.1 - Find d2ydx2. y=x2+1Ch. 3.1 - Find d2ydx2 y=xx+1Ch. 3.1 - Find d2ydx2 y=22+x2Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - In Exercises 4144, a function h(x) is defined in...Ch. 3.1 - Volume An open rectangular box is 3 feet long and...Ch. 3.1 - Volume A closed rectangular box is to be...Ch. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Average Revenue Let R(x) be the revenue received...Ch. 3.1 - Average Velocity Let s(t) be the number of miles a...Ch. 3.1 - Prob. 51ECh. 3.1 - Cost-Benefit of Emission Control A manufacturer...Ch. 3.1 - In Exercises 53 and 54, use the fact that at the...Ch. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - If f(x) and g(x) are differentiable functions such...Ch. 3.1 - If f(x) and g(x) are differentiable functions such...Ch. 3.1 - Prob. 62ECh. 3.1 - Let f(x)=1/x and g(x)=x3. Show that the product...Ch. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.2 - Consider the function h(x)=(2x35)5+(2x35)4 Write...Ch. 3.2 - Consider the function h(x)=(2x35)5+(2x35)4 Compute...Ch. 3.2 - Prob. 3CYUCh. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Compute f(g(x)), where f(x) and g(x) are the...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Each of following functions may be viewed as a...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - Differentiate the functions in Exercises 1120...Ch. 3.2 - In Exercises 2126, a function h(x) is defined in...Ch. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - In Exercises 2126, a function h(x) is defined in...Ch. 3.2 - In Exercises 2126, a function h(x) is defined in...Ch. 3.2 - Prob. 26ECh. 3.2 - Sketch the graph of y=4x/(x+1)2,x1.Ch. 3.2 - Sketch the graph of y=2/(1+x2)Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute ddxf(g(x)), where f(x) and g(x) are...Ch. 3.2 - Compute dydx using the chain rule in formula (1)....Ch. 3.2 - Compute dydx using the chain rule in formula (1)....Ch. 3.2 - Compute dydx using the chain rule in formula (1)....Ch. 3.2 - Prob. 40ECh. 3.2 - Compute dydxt=t0 y=x23x,x=t2+3,t0=0Ch. 3.2 - Compute dydxt=t0 y=(x22x+4)2,x=1t+1,t0=1Ch. 3.2 - Compute dydxt=t0 y=x+1x1,x=t24,t0=3Ch. 3.2 - Prob. 44ECh. 3.2 - Find the equation of the line tangent to the graph...Ch. 3.2 - Find the equation of the line tangent to the graph...Ch. 3.2 - Find the x- coordinate of all points on the curve...Ch. 3.2 - The function f(x)=x26x+10 has one relative minimum...Ch. 3.2 - Prob. 49ECh. 3.2 - Allometric Equation Many relations in biology are...Ch. 3.2 - Suppose that P, y and t are variables, where P is...Ch. 3.2 - Suppose that Q, x and y are variables, where Q is...Ch. 3.2 - Marginal Profit and Times Rate of Change When a...Ch. 3.2 - Marginal Cost and Time Rate of Change The cost of...Ch. 3.2 - A model for Carbon Monoxide Levels Ecologists...Ch. 3.2 - Profit A manufacturer of microcomputers estimates...Ch. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - If f(x) and g(x) are differentiable functions,...Ch. 3.2 - Prob. 60ECh. 3.2 - Effect of Stocks on Total Assets of a Company...Ch. 3.2 - Refer to Exercise 61. Use chain rule to find...Ch. 3.2 - Refer to Exercise 61. Find dxdt|t=2.5 and...Ch. 3.2 - Refer to Exercise 61. What was the maximum value...Ch. 3.2 - In an expression of the form f(g(x)), f(x) is...Ch. 3.3 - Solution can be found following the section...Ch. 3.3 - Solution can be found following the section...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - In Exercise 1-18, suppose that x and y are related...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Use implicit differentiation of the equation in...Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - Find the equation of the tangent line to the graph...Ch. 3.3 - Slope of the Lemniscate The graph of...Ch. 3.3 - The graph of x4+2x2y2+y4=9x29y2 is a lemniscate...Ch. 3.3 - Marginal Rate of Substitution Suppose that x and y...Ch. 3.3 - Demand Equation Suppose that x and y represents...Ch. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - Prob. 34ECh. 3.3 - In Exercise 31 36, suppose that x and y are both...Ch. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Demand Equation Suppose that the price p (in...Ch. 3.3 - Demand Equation Suppose that the price p (in...Ch. 3.3 - Advertising Affects Revenue The monthly...Ch. 3.3 - Rate of Change of Price Suppose that in Boston the...Ch. 3.3 - Related Rates Figure 7 shows a 10- foot ladder...Ch. 3.3 - Related Rates An airplane flying 390 feet per...Ch. 3.3 - Related Rates A baseball diamond is a 90- foot by...Ch. 3.3 - Related Rates A motorcyclist is driving over a...Ch. 3 - State the product rule and quotient rule.Ch. 3 - Prob. 2FCCECh. 3 - Prob. 3FCCECh. 3 - Prob. 4FCCECh. 3 - Prob. 5FCCECh. 3 - Prob. 6FCCECh. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions. y=x(x51)3Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions. y=xx+4Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions....Ch. 3 - Differentiate the following functions. y=x26xx2Ch. 3 - Differentiate the following functions. y=2x23xCh. 3 - Differentiate the following functions. y=(3x2x3)2Ch. 3 - Differentiate the following functions. y=x3+xx2xCh. 3 - Let f(x)=(3x+1)4(3x)5. Find all x such that...Ch. 3 - Let f(x)=x2+1x2+5. Find all x such that f(x)=0.Ch. 3 - Find the equation of the line tangent to the graph...Ch. 3 - Find the equation of the line tangent to the graph...Ch. 3 - Minimizing Area A botanical display is to be...Ch. 3 - Repeat Exercise 17, with the sidewalk on the...Ch. 3 - Cost function A store estimates that its cost when...Ch. 3 - Rate of Change of Taxes A company pays y dollars...Ch. 3 - In Exercise 21-23, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 21-23, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 21-23, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 24-26, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 24-26, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 24-26, find a formula for ddxf(g(x)),...Ch. 3 - In Exercise 27-29, find dydx, where y is a...Ch. 3 - In Exercise 27-29, find dydx, where y is a...Ch. 3 - In Exercise 27-29, find dydx, where y is a...Ch. 3 - In Exercises 30 32, find dydx, where y is a...Ch. 3 - In Exercises 30 32, find dydx, where y is a...Ch. 3 - In Exercises 30 32, find dydx, where y is a...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Exercises 33 38 refer to the graphs of the...Ch. 3 - Revenue Function The revenue, R, that a company...Ch. 3 - Amount of Drug Usage The amount, A, of anesthetics...Ch. 3 - The graph of x2/3+y2/3=8 is the astroid in Fig. 3...Ch. 3 - Slope of the Folium of Descartes The graph of...Ch. 3 - Slope of the Folium of Descartes The graph of...Ch. 3 - In Exercises 43-46, x and y are related by the...Ch. 3 - In Exercises 43-46, x and y are related by the...Ch. 3 - In Exercises 43-46, x and y are related by the...Ch. 3 - Cost Analysis and Production A factorys weekly...Ch. 3 - Use of Books at a Library A town library estimates...Ch. 3 - Demand equation Suppose that the price p and...Ch. 3 - Volume of an Oil Spill An offshore oil well is...Ch. 3 - Weight and Surface Area Animal physiologists have...Ch. 3 - Sales and Advertising Suppose that a kitchen...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- The function s(t) represents the position of an object at time t moving along a line. Suppose s(1) = 116 and s(5)=228. Find the average velocity of the object over the interval of time [1,5]. The average velocity over the interval [1,5] is Vav = (Simplify your answer.)arrow_forwardFor the position function s(t) = - 16t² + 105t, complete the following table with the appropriate average velocities. Then make a conjecture about the value of the instantaneous velocity at t = 1. Time Interval Average Velocity [1,2] Complete the following table. Time Interval Average Velocity [1, 1.5] [1, 1.1] [1, 1.01] [1, 1.001] [1,2] [1, 1.5] [1, 1.1] [1, 1.01] [1, 1.001] ப (Type exact answers. Type integers or decimals.) The value of the instantaneous velocity at t = 1 is (Round to the nearest integer as needed.)arrow_forwardFind the following limit or state that it does not exist. Assume b is a fixed real number. (x-b) 40 - 3x + 3b lim x-b x-b ... Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (x-b) 40 -3x+3b A. lim x-b x-b B. The limit does not exist. (Type an exact answer.)arrow_forward
- x4 -289 Consider the function f(x) = 2 X-17 Complete parts a and b below. a. Analyze lim f(x) and lim f(x), and then identify the horizontal asymptotes. x+x X--∞ lim 4 X-289 2 X∞ X-17 X - 289 lim = 2 ... X∞ X - 17 Identify the horizontal asymptotes. Select the correct choice and, if necessary, fill in the answer box(es) to complete your choice. A. The function has a horizontal asymptote at y = B. The function has two horizontal asymptotes. The top asymptote is y = and the bottom asymptote is y = ☐ . C. The function has no horizontal asymptotes. b. Find the vertical asymptotes. For each vertical asymptote x = a, evaluate lim f(x) and lim f(x). Select the correct choice and, if necessary, fill in the answer boxes to complete your choice. earrow_forwardExplain why lim x²-2x-35 X-7 X-7 lim (x+5), and then evaluate lim X-7 x² -2x-35 x-7 x-7 Choose the correct answer below. A. x²-2x-35 The limits lim X-7 X-7 and lim (x+5) equal the same number when evaluated using X-7 direct substitution. B. Since each limit approaches 7, it follows that the limits are equal. C. The numerator of the expression X-2x-35 X-7 simplifies to x + 5 for all x, so the limits are equal. D. Since x²-2x-35 X-7 = x + 5 whenever x 7, it follows that the two expressions evaluate to the same number as x approaches 7. Now evaluate the limit. x²-2x-35 lim X-7 X-7 = (Simplify your answer.)arrow_forwardA function f is even if f(x) = f(x) for all x in the domain of f. If f is even, with lim f(x) = 4 and x-6+ lim f(x)=-3, find the following limits. X-6 a. lim f(x) b. +9-←x lim f(x) X-6 a. lim f(x)= +9-←x (Simplify your answer.) b. lim f(x)= X→-6 (Simplify your answer.) ...arrow_forwardEvaluate the following limit. lim X-X (10+19) Select the correct answer below and, if necessary, fill in the answer box within your choice. 10 A. lim 10+ = 2 ☐ (Type an integer or a simplified fraction.) X-∞ B. The limit does not exist.arrow_forwardFind the following limit or state that it does not exist. x² +x-20 lim x-4 x-4 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. lim x²+x-20 x-4 (Type an exact answer.) x→4 B. The limit does not exist.arrow_forwardDetermine the intervals on which the following function is continuous. f(x) = x - 5x + 6 2 X-9 On what interval(s) is f continuous? (Simplify your answer. Type your answer in interval notation. Use a comma to separate answers as needed.)arrow_forwardFind the following limit or state that it does not exist. 2 3x² +7x+2 lim X-2 6x-8 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. lim 3x²+7x+2 6x-8 (Simplify your answer.) X-2 B. The limit does not exist.arrow_forwardFind the following limit or state that it does not exist. X-2 lim x-2 5x+6 - 4 Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. lim X-2 X-2 15x+6 = (Type an exact answer.) - 4 B. The limit does not exist.arrow_forward(a) Sketch the graph of a function that is not continuous at 1, but is defined at 1. (b) Sketch the graph of a function that is not continuous at 1, but has a limit at 1. (a) Which of the following graphs shows a function that is not continuous at 1, but is defined at 1. ○ A. Ay ✓ B. 5 X ✓ (b) Which of the following graphs shows a function that is not continuous at 1, but has a limit at 1. ○ A. B. X y 5- -5 5 ✓ ✓ 5 ☑ 5 X y ☑ LVarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
What is a Relation? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=hV1_wvsdJCE;License: Standard YouTube License, CC-BY
RELATIONS-DOMAIN, RANGE AND CO-DOMAIN (RELATIONS AND FUNCTIONS CBSE/ ISC MATHS); Author: Neha Agrawal Mathematically Inclined;https://www.youtube.com/watch?v=u4IQh46VoU4;License: Standard YouTube License, CC-BY