Chapter 31, Problem 17PQ

To determine

The contribution to the circulation integral due to each segment of the loop, and the net current through the loop that must be present.

Answer to Problem 17PQ

The contribution of side 1 is $0.0313\text{ T}\cdot \text{m}$ , the contribution of side 2 is $-0.0438\text{ T}\cdot \text{m}$ , the contribution of side 3 is $-0.0313\text{ T}\cdot \text{m}$ and the contribution of side 4 is $0.0438\text{ T}\cdot \text{m}$.

Explanation of Solution

Draw the figure for the system as shown below:

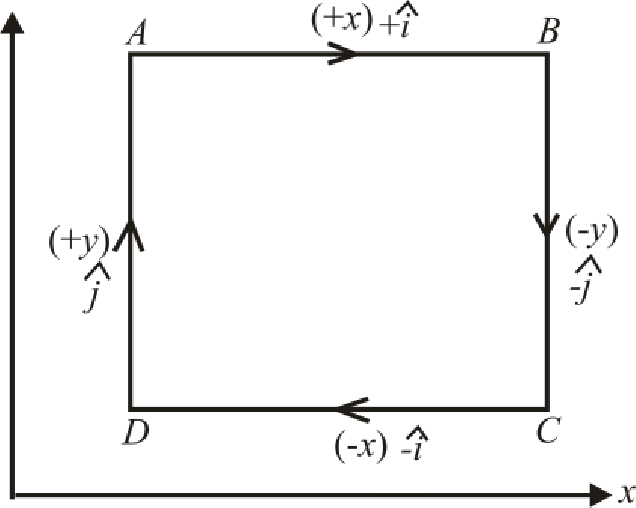
Refer to the above figure, consider a square loop $ABCD$ in $xy\text{-plane}$. The sides $AB$ and $CD$ have equal magnitude in opposite direction whereas side $BC$ and side $DA$ has equal magnitude in opposite direction.

Write the general expression for Ampere’s Circuital Law for the given above figure as.

    ${\mu }_0{I}_{thru}={\displaystyle \oint \overrightarrow{B}}.\overrightarrow{dl}$                                                                                              (I)

Here, $\overrightarrow{dl}$ is length of element, ${\mu }_0$ is the permittivity of free space, $I_{thru}$ is the current through the conductor and $\overrightarrow{B}$ is magnetic field.

Substitute $dx\widehat{i}$ for $\overrightarrow{dl}$ in equation (I) for side $AB$ as.

    ${\left({\mu }_0{I}_{thru}\right)}_{AB}={\displaystyle \underset{A}{\overset{B}{\int }}\overrightarrow{B}.dx\widehat{i}}$                                                                                    (II)

Substitute $dy\left(-\widehat{j}\right)$ for $\overrightarrow{dl}$ in equation (I) for side $BC$ as.

    ${\left({\mu }_0{I}_{thru}\right)}_{BC}={\displaystyle \underset{B}{\overset{C}{\int }}\overrightarrow{B}.\left(-dy\right)\widehat{j}}$                                                                           (III)

Substitute $dx\left(-\widehat{i}\right)$ for $\overrightarrow{dl}$ in equation (I) for side $CD$ as.

    ${\left({\mu }_0{I}_{thru}\right)}_{CD}={\displaystyle \underset{C}{\overset{D}{\int }}\overrightarrow{B}.\left(-dx\right)\widehat{i}}$                                                                             (IV)

Substitute $dy\left(\widehat{j}\right)$ for $\overrightarrow{dl}$ in equation (I) for side $DA$ as.

    ${\left({\mu }_0{I}_{thru}\right)}_{DA}={\displaystyle \underset{D}{\overset{A}{\int }}\overrightarrow{B}.dy\widehat{j}}$                                                                                     (V)

Conclusion:

 Substitute $\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{}\text{T}$ for $\overrightarrow{B}$ and $2.50\text{ cm}\widehat{i}$ for ${\displaystyle \int dx\widehat{i}}$ in equation (II).

     $\begin{array}{c}{\left({\mu }_0{I}_{thru}\right)}_{AB}=\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{}\text{T}\right)\cdot \left(2.50\text{ cm}\right)\widehat{i}\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}\right)\cdot \left(2.50\text{ cm}\left(\frac{1\text{ m}}{100\text{ cm}}\right)\right)\widehat{i}\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}\right)\cdot \left(0.025\text{m}\right)\widehat{i}\\ =0.03125\text{ T}\cdot \text{m}\end{array}$

 Further,simplify the above equation as.

     ${\left({\mu }_0{I}_{thru}\right)}_{AB}=0.0313\text{ T}\cdot \text{m}$

 Thus, contribution of side $AB$ is $\underset{\_}{0.0313\text{ T}\cdot \text{m}}$.

 Substitute $\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}$ for $\overrightarrow{B}$ and $2.50\text{ cm}\left(-\widehat{j}\right)$ for ${\displaystyle \int dy\left(-\widehat{j}\right)}$ in equation (III).

     $\begin{array}{c}{\left({\mu }_0{I}_{thru}\right)}_{BC}=\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}\right)\cdot \left(2.50\text{ cm}\right)\left(-\widehat{j}\right)\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}\right)\cdot \left(2.50\text{ cm}\left(\frac{1\text{ m}}{100\text{ cm}}\right)\right)\left(-\widehat{j}\right)\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}\right)\cdot \left(0.025\text{ m}\right)\left(-\widehat{j}\right)\\ =-0.0438\text{ T}\cdot \text{m}\end{array}$

 Further,simplify the above equation as.

     ${\left({\mu }_0{I}_{thru}\right)}_{BC}=-0.0438\text{ T}\cdot \text{m}$

 Thus, contribution of side $BC$ is $\underset{\_}{-0.0438\text{ T}\cdot \text{m}}$.

 Substitute $\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}$ for $\overrightarrow{B}$ and $2.50\text{ cm}\left(-\widehat{i}\right)$ for ${\displaystyle \int dx\left(-\widehat{i}\right)}$ in equation (IV).

     $\begin{array}{c}{\left({\mu }_0{I}_{thru}\right)}_{CD}=\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{ T}\right)\cdot \left(2.50\text{ cm}\right)\left(-\widehat{i}\right)\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{ T}\right)\cdot \left(2.50\text{ cm}\times \frac{1\text{ m}}{100\text{ cm}}\right)\left(-\widehat{i}\right)\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{ T}\right)\cdot \left(0.025\text{ m}\right)\left(-\widehat{i}\right)\\ =-0.03125\text{ T}\cdot \text{m}\end{array}$

 Further,simplify the above equation as.

     ${\left({\mu }_0{I}_{thru}\right)}_{CD}=-0.0313\text{ T}\cdot \text{m}$

 Thus, the contribution of side $CD$ is $\underset{\_}{-0.0313\text{ T}\cdot \text{m}}$.

 Substitute $\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{T}$ for $\overrightarrow{B}$ and $\left(2.50\text{ cm}\right)\widehat{j}$ for ${\displaystyle \int dy\widehat{j}}$ in equation (V).

     $\begin{array}{c}{\left({\mu }_0{I}_{thru}\right)}_{DA}=\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{ T}\right)\cdot \left(2.50\text{ cm}\right)\widehat{j}\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{ T}\right)\cdot \left(2.50\text{ cm}\left(\frac{1\text{ m}}{100\text{ cm}}\right)\right)\widehat{j}\\ =\left(\left(1.25\widehat{i}+1.75\widehat{j}\right)\text{ T}\right)\cdot \left(0.025\text{}\text{m}\right)\widehat{j}\\ =0.0438\text{ T}\cdot \text{m}\end{array}$

 Further,simplify the above equation as.

     ${\left({\mu }_0{I}_{thru}\right)}_{DA}=0.0438\text{ T}$

 Thus, the contribution of side $AB$ is $\underset{\_}{0.0438\text{ T}}$.

 Thus, the contribution of side 1 is $0.0313\text{ T}\cdot \text{m}$ , the contribution of side 2 is $-0.0438\text{ T}\cdot \text{m}$ , the contribution of side 3 is $-0.0313\text{ T}\cdot \text{m}$ and the contribution of side 4 is $0.0438\text{ T}\cdot \text{m}$.