
Concept explainers
To calculate: The temperature distribution in a rod as shown in figure below with internal heat generation using the finite-element method and also derive the element nodal equations using Fourier heat conduction.
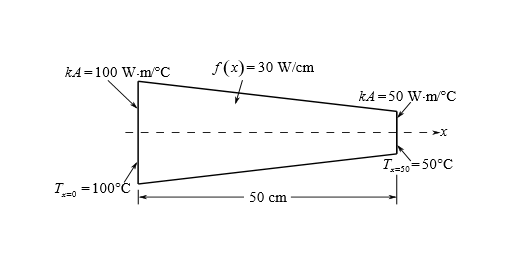
Answer to Problem 12P
Solution: The temperature distribution in a rod at various nodes is shown below,

Explanation of Solution
Given Information:
To develop nodal equations for the temperature and their gradients at each of the six nodes. The element nodal equations is given as,
With the heat conservation relationships is,
Here,
The given rod is 50 cm long, the x-coordinate is positive to the right end and zero at the left end,
Calculation:
The element 1 the equations for the node 1 and node 2 is,
Solve the equation for node 1,
Substitute the value from given data,
Change the temperature so the equation becomes,
Solve the equation for the node 2,
Substitute the values from given data,
So, the equation of node 2 is,
Similarly, the value for other nodes is calculated. For element 2 at node 2,
Substitute the values from given data,
Change the state so the equation becomes,
Derive for node 3,
Substitute the values from given data,
So, the equation of node 3 is,
Derive the equation for the element 3,
Node 3
Substitute the values from given data,
Change the state so the equation becomes,
Derive for node 4,
Substitute the values from given data,
So, the equation of node 4 is,
Derive the equation for the element 4,
The equations for node 4 is,
Substitute the values from given data,
Change the state so the equation becomes,
Derive the equation for the node 5,
Substitute the values from given data,
So, the equation of node 5 is,
Derive the equation for the element 5,
For node 5,
Substitute the values from given data,
Change the state so the equation becomes,
Derive the equation for node 6,
Substitute the values from given data,
So, the equation of node 6 is,
The equation assembly is given as,
Insert the boundary conditions then the matrix becomes,
Use MATLAB to write code for solving the matrix,

The desired output is,

Want to see more full solutions like this?
Chapter 31 Solutions
Numerical Methods for Engineers
- If you were asked to load 225 boxes onto a truck, and the boxes are crated, with each crate containing nine boxes, how many crates would you need to load?arrow_forwardHabitat for Humanity International is a nonprofit organization dedicated to eliminating poverty housing worldwide. Suppose the following table contains estimates of activity times (in days) involved in the construction of a house that Habitat for Humanity is building. Activity Optimistic Most Probable Pessimistic A 6 7.0 8 B 7 8.0 9 C 7 7.5 11.5 D 7 9.0 10 E 6 7.0 9 F 3 4.0 5 (a) Compute the expected activity completion times and the variance for each activity. (Round your answers to two decimal places.) Activity Expected Times A B C D E F Variance (b) An analyst determined that the critical path consists of activities B-D-F. Compute the expected project completion time and the variance of this path. (Round your answers to two decimal places.) expected project completion time variance of projection completion timearrow_forwardTo manage the production of an animated movie, Pixar Animation Studios has listed the major activities involved, the predecessor relationships, and activity times (in months). The project is completed when activities F and G are both complete. Activity Immediate Predecessor G A B CD E A A C, B C, B D, E Time 4 6 2 6 3 3 5 (a) Find the critical path. (Enter your answers as a comma-separated list.) (b) The project must be completed in 1.5 years. Do you anticipate difficulty in meeting the deadline? Explain. The critical path activities require months to complete. Thus the project ---Select--- be completed in 1.5 years.arrow_forward
- To help with preparations, a couple has devised a project network to describe the activities that must be completed by their wedding date. In addition, they have estimated the time of each activity (in weeks). Start D F B E G Activity A B C DEFGH Time 5 3 6 6 6 3 11 10 (a) Identify the critical path. (Enter your answers as a comma-separated list.) H Finish (b) How much time (in weeks) will be needed to complete this project? week(s) (c) Can activity D be delayed without delaying the entire project? If so, by how many weeks? (If the activity can not be delayed, enter 0.) week(s) (d) Can activity C be delayed without delaying the entire project? If so, by how many weeks? (If the activity can not be delayed, enter 0.) week(s) (e) What is the schedule for activity E (in weeks)? Earliest Start Latest Start Earliest Finish Latest Finish week(s) week(s) week(s) week(s)arrow_forward30.6. Classify the zeros and singularities of the functions tanz (a). f(z)=sin(1-2-1), (b). f(2) = (c). f(z)= tanh .arrow_forward1. Locate the singularities of three of the following functions, and determine their type. (a) f(z)=2(z-sinz). (b) f(z) = (-) (c) f(z) = (z+2-22²)-1 (d) f(z) = sinzarrow_forward
- Q 2/classify the zeros and poles of the function f(z) = tanz Zarrow_forward30.1. Show that z = 0 is a removable singularity of the following functions. Furthermore, define f(0) such that these functions are analytic at z = 0. (a). f(z) = 2 sin z- z 1-12² - cos z (b). f(z) = (c). f(z) = sin 22arrow_forward3. Consider the polynomial equation 6-iz+7z² -iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forward
- 30.3. Find and classify the isolated singularities of the following func- tions: (a). 23+1 22(2-1) (b). ²e¹/, (c). sin 3z (d). COS 2arrow_forward3. Consider the polynomial equation 6-iz+7z2-iz³ +z = 0 for which the roots are 3i, -2i, -i, and i. (a) Verify the relations between this roots and the coefficients of the polynomial. (b) Find the annulus region in which the roots lie.arrow_forwardDetermine the set of odd primes p for which 23 is a quadratic residue.arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






